„Analiza trendu czasowego cen gruntów na przykładzie Bielan Wrocławskich”

Podstawowym zadaniem jakie stoi przed inwestorem działającym na rynku nieruchomości jest ustalenie przyszłej wartości nieruchomości stanowiącej przedmiot ewentualnej inwestycji. Jedną z metod prognozy zmiany wartości jest analiza historycznych cen transakcyjnych zakończona wyznaczeniem funkcji trendu opisującej zależność cen rynkowych od upływu czasu. Wyznaczona tak funkcja regresji umożliwia prognozę zmian cen i wartości nierucho-mości w najbliższej przyszłości. Metoda ta ma szereg zastosowań; z tego typu analiz mogą korzystać zarówno inwestorzy jak też np. rzeczoznawcy majątkowy - przykładowo, gdy przedmiotem wyceny jest nieruchomość mająca stanowić zabezpieczenie hipoteczne udzielanego kredytu, zaś bank zainteresowany jest spodziewaną przyszłą wartością nieruchomości (w dniu egzekucji z nieruchomości w przypadku niespłacenia przez kredytobiorcę kredytu). Tego typu modele matematyczne mogą być również wykorzystywane przy masowej wycenie nieruchomości, np. dla potrzeb aktualizacji opłat za użytkowanie wieczyste gruntów.

Artykuł niniejszy jest przykładem takiej analizy; składa się on z dwóch części. W pierwszej części autor poddał analizie ceny transakcyjne gruntów, jakie miały miejsce w latach 1995 - 1998 w miejscowości Bielany Wrocławskie. Wynikiem przeprowadzonej analizy są wyznaczone funkcje trendu czasowego (liniowa, wykładnicza oraz liniowa z uwzględnionymi wahaniami sezonowymi) oraz, dokonana w oparciu o tak wyznaczone funkcje, prognoza wzrostu cen gruntów w okresie III kwartał 1998 - I kwartał 1999 r. Wyznaczone funkcje trendu czasowego zostały przez autora wykorzystane m.in. przy szacowaniu nieruchomości zlokalizowanych w pasie drogowym autostrady A-4 nabywanych przez Agencję Budowy i Eksploatacji Autostrad na rzecz Skarbu Państwa w drodze umów cywilno - prawnych. Druga część artykułu, to analiza cen transakcyjnych gruntów z okresu ww. prognozy, wraz z odpowiedzią na pytanie na ile przewidywania dotyczące zmian cen nieruchomości gruntowych okazały się trafne.

W pierwszym etapie dokonana została szczegółowa analiza transakcji sprzedaży nierucho-mości w Bielanach Wrocławskich (węzeł komunikacyjny na autostradzie A-4 przy zjeździe do Wrocławia) zawartych w okresie od III kwartału 1995 roku do II kwartału 1998 roku. Wszystkie sprzedaże, które stanowić miały podstawę do analizy trendu czasowego, zostały starannie przeanalizowane. Z dalszych rozważań wyłączone zostały te transakcje, które autor nie uznał za reprezentatywne. Należą do nich m.in.:

1. Sprzedaże lokali mieszkalnych na rzecz dotychczasowych najemców.

2. Transakcje sprzedaży nieruchomości o charakterze rolnym.

3. Uwłaszczenia przedsiębiorstw państwowych i spółdzielni na nieruchomościach.

W oparciu o tak przyjęte ograniczenia do dalszej analizy przyjęte zostały 94 transakcje kupna-sprzedaży działek budowlanych. Ponieważ poszczególne działki różniły się dość znacznie powierzchnią, w celu ujednolicenia nieruchomości stanowiących bazę porównawczą autor ograniczył się do działek o powierzchniach z przedziału od 400 do 1000 m². W badanym okresie odbyły 53 transakcje takimi działkami. Następnie, dla każdego z kwartałów wyzna-czona została średnia ważona jednostkowych cen sprzedaży 1m² gruntu działek, gdzie wagę stanowiły powierzchnie działek (średnie ważone zostały przyjęte, gdyż zdaniem autora ceny sprzedaży większych działek w większym stopniu kreują rynek nieruchomości niż ceny sprzedaży małych nieruchomości).

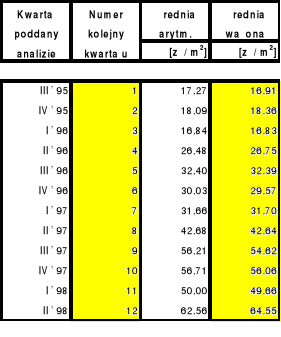
Tabela 1 (zestawienie średnich jednostkowych cen sprzedaży dla kolejnych kwartałów):

W oparciu o tak przygotowane dane wykonano wykres cen transakcyjnych. Obserwując kształt uzyskanego wykresu przyjęto wstępnie, że analizie zostaną poddane trzy funkcje regresji: liniowa, logarytmiczna oraz wykładnicza.

Odpowiednie wzory funkcji przedstawiają się następująco (gdzie B i M to szukane stałe):

1) regresja liniowa: y = B + M * x

2) regresja logarytmiczna: y = B + M * ln (x)

3) regresja wykładnicza: y = B * e ^{M * x}

Dla tak przyjętych funkcji otrzymano następujące wyniki:

Lp.	Funkcja regresji	Stała M	Stała B	Wsp. korelacji
1.	liniowa	4,38	8,20	0,96
2.	logarytmiczna	19,00	5,02	0,87
3.	wykładnicza	0,12	15,62	0,96

Biorąc pod uwagę wartość współczynnika korelacji, wyznaczonego dla każdej z funkcji, przyjęto do dalszej analizy funkcję liniową oraz wykładniczą; pominięta natomiast została funkcja logarytmiczna.

W oparciu o wyznaczone funkcje można dokonać prognozy przeciętnych (średnich) cen np. w okresie III kwartał 1998 roku - I kwartał 1999 r. Zgodnie ze wzorami odpowiednich funkcji regresji prognozowana średnia cena jednostkowa 1m² gruntu w Bielanach Wrocławskich kształtuje się w sposób następujący:

Funkcja trendu	Wzór funkcji	III kw. 1998 r.	IV kw. 1998 r.	I kw. 1999 r.
liniowa	y = B + M * x	65,14 zł / 1m^2	69,52 zł / 1m^2	73,90 zł / 1m^2
wykładnicza	y = B * e ^M * x	74,33 zł / 1m^2	83,81 zł / 1m^2	94,50 zł / 1m^2

Tabela 2 (ceny sprzedaży wyznaczone w oparciu o funkcję regresji liniowej i wykładniczej):

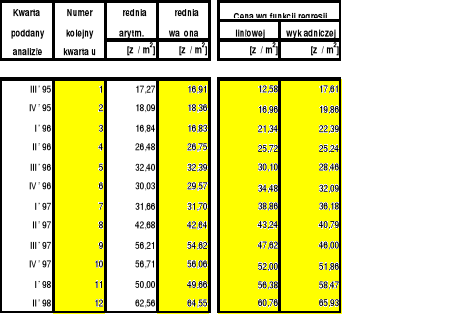
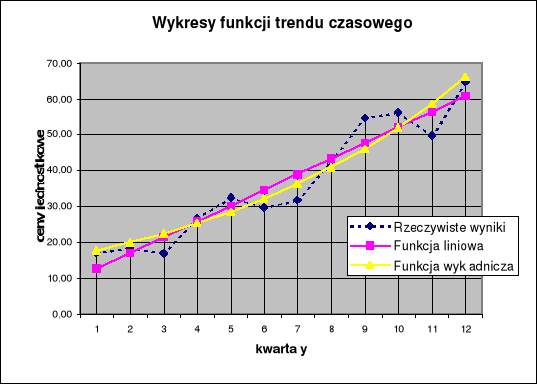
Rysunek 1 (wykres średnich cen sprzedaży oraz funkcji regresji liniowej i wykładniczej):

Analizując kształt wykresu tych funkcji regresji, jak również wykresu rzeczywistych cen transakcyjnych (pod postacią średnich ważonych cen wyznaczonych dla poszczególnych kwartałów) widać, że w analizowanym przedziale czasowym obydwie funkcje (tj. liniowa i wykładnicza) charakteryzują się podobnym przebiegiem. Jeśli jednak przyjrzeć się wykresowi uważniej zaobserwować można pewną prawidłowość, a mianowicie że rzeczywiste ceny są wyższe od uzyskanych przy pomocy funkcji regresji liniowej w kwartale 1, 5 i 9. Odpowiada to trzecim kwartałom roku 1995, 1996 i 1997. Należy się zatem spodziewać, że również dla x = 13 (odpowiada to III kwartałowi 1998 r.) ceny rzeczywiste „wyskoczą” powyżej wykresów obydwu funkcji. Co więcej, w kwartałach 3, 7 i 11 rzeczywiste ceny transakcyjne są z kolei niższe niż ceny interpolowane przy użyciu funkcji regresji liniowej. Widać wreszcie, że obydwa odstępstwa pojawiają się w równych okresach co 4 kwartały. Może to oznaczać, że oprócz generalnego trendu wzrostowego opisanego np. funkcją liniową występują również wahania cykliczne, w tym przypadku sezonowe. Chcąc zatem jeszcze lepiej wyznaczyć funkcję opisującą trend czasowy należy uwzględnić te wahania. Poniżej przedstawiono jedną z metod postępowania; szerzej jest ona opisana w [1]:

1. Wyznaczenie średnich ruchomych scentrowanych

2. Obliczenie, dla każdego badanego okresu, indywidualnego wskaźnika sezonowości

3. Wyznaczenie surowych (nie oczyszczonych) wskaźników wahań sezonowych

4. Wyznaczenie współczynnika korygującego wskaźniki wahań sezonowych

5. Wyznaczenie oczyszczonych (skorygowanych) wskaźników wahań sezonowych

6. Wyznaczenie funkcji trendu głównego (oczyszczonego z wahań sezonowych)

7. Wyznaczenie trendu główny z uwzględnionymi wskaźnikami wahań sezonowych

W wyniku obliczeń wykonanych zgodnie z ww. procedurą wyznaczono skorygowane (oczyszczone) wskaźniki sezonowości, które wynoszą odpowiednio:

okres 1 (III kwartały): 113,65 * 1,00706 = 114,45%

okres 2 (IV kwartały): 98,48 * 1,00706 = 99,18%

okres 3 (I kwartały): 81,88 * 1,00706 = 82,46%

okres 4 (II kwartały): 103,18 * 1,00706 = 103,91%

Dla szeregu wartości oczyszczonych z wahań sezonowych, wyznaczono funkcję regresji liniowej. Otrzymana funkcja (B = 7,29, M = 4,17, gdzie funkcja regresji liniowej wyraża się wzorem y = B + M * x) po uwzględnieniu wskaźników sezonowości stanowi poszukiwaną funkcję trendu, której wykres znajduje się na rysunku nr 2. Obserwowany na wykresie zakres zbieżności pomiędzy zaobserwowanymi danymi (wykresem cen rzeczywistych) a wynikami obliczeń (wykresem funkcji trendu) nie pozostawia wątpliwości co do jakości wyznaczonej funkcji. Potwierdza to również wyznaczony współczynnik korelacji, który wynosi 0,99. Można zatem przyjąć, że wyznaczona funkcja regresji z uwzględnieniem wahań cyklicznych dobrze oddaje trend czasowy - wzrost cen nieruchomości w analizowanym przedziale czasowym.

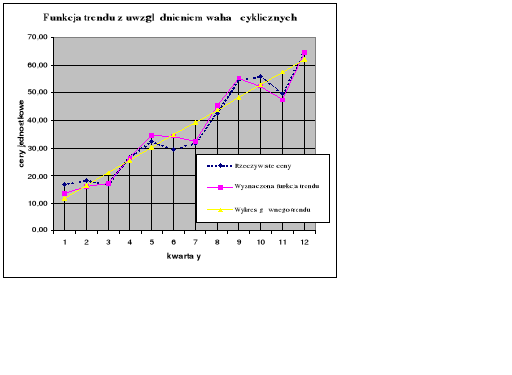
Rysunek 2 (wykres cen sprzedaży oraz funkcji trendu z uwzględnieniem wahań cyklicznych):

Pozostaje na koniec wykonanie, w oparciu o wyznaczoną funkcję, prognozy średnich cen jednostkowych w następnych trzech kwartałach. Prognoza ta przedstawia się następująco:

III kwartał 1998 r.: (7,29 + 4,17 * 13) * 114,45% = 70,37 zł / m²

IV kwartał 1998 r.: (7,29 + 4,17 * 14) * 99,18% = 65,13 zł / m²

I kwartał 1999 r.: (7,29 + 4,17 * 15) * 82,46% = 57,59 zł / m²

* * *

Poniższa część artykułu, to analiza cen transakcyjnych gruntów jakie miały miejsce w miejscowości Bielany Wrocławskie w okresie od III kwartału 1998 r. do I kwartału 1999 r., wraz z odpowiedzią na pytanie na ile przewidywania dotyczące zmian cen nieruchomości gruntowych (część 1 artykułu) okazały się trafne. Analogicznie jak dla danych z pierwszej części artykułu pominięto transakcje, które nie zostały uznane za wolnorynkowe oraz ograniczono się do sprzedaży działek o powierzchni równej od 400 do 1 000 m².

Obserwowane ceny i wcześniejsze prognozy cenowe zawarte są w poniższym zestawieniu:

Funkcja trendu	III kw. 1998 r.	IV kw. 1998 r.	I kw. 1999 r.
rzeczywiste ceny gruntu	86,57 zł / 1m^2	78,98 zł / 1m^2	77,34 zł / 1m^2
regresja liniowa	65,14 zł / 1m^2	69,52 zł / 1m^2	73,90 zł / 1m^2
regresja wykładnicza	74,33 zł / 1m^2	83,81 zł / 1m^2	94,50 zł / 1m^2
regresja liniowa z uwzględnienymi wahaniami sezonowymi	70,35 zł / 1m^2	65,13 zł / 1m^2	57,59 zł / 1m^2

Po wstępnym zapoznaniu się z powyższymi cenami (tak transakcyjnymi jak i prognozowanymi) widać, że, generalnie rzecz biorąc prognoza zmian cen gruntu okazała się zadowalająca. Poza pierwszym badanym okresem, gdzie ceny gruntu były znacznie wyższe niż zakładała prognoza, w pozostałych kwartałach różnice pomiędzy rzeczywistymi cenami a wynikami ekstrapolacji były stosunkowo niewielkie (w zależności od przyjętej funkcji regresji). Należy przy tym pamiętać, jak skomplikowanym rynkiem jest rynek nieruchomości, tj. jak wiele czynników potrafi oddziaływać na siły popytu i podaży (regulacje prawno - podatkowe, polityka makroekonomiczna - sprzedaż nieruchomości inwestorom zagranicznym, rozwój autostrad płatnych itp.). Biorąc to wszystko pod uwagę można stwierdzić, że z punktu widzenia inwestorów działających na rynku nieruchomości dokładność tak wykonanej prognozy jest do przyjęcia. Analizując otrzymane wyniki łatwo ponadto zauważyć, że:

1. Zaobserwowane rzeczywiste ceny transakcyjne są, zwłaszcza w pierwszym okresie, znacznie wyższe niż wyniki uzyskane przy użyciu funkcji regresji, zwłaszcza przy użyciu funkcji regresji liniowej.

2. W trzecim z analizowanych okresów funkcja regresji liniowej dała wynik bardziej zbliżony cenom rzeczywistym, niż funkcja regresji wykładniczej.

3. Analizowane ceny transakcyjne w 3 ostatnich kwartałach wykazują tendencję spadkową (w każdym kolejnym kwartale ceny są niższe); jest to zgodne z wynikami uzyskanymi dla funkcji liniowej z uwzględnionymi wahaniami sezonowymi. Z drugiej strony zdecydowanie największym błędem okazała się prognoza cen uzyskana właśnie dla funkcji liniowej z uwzględnionymi wahaniami sezonowymi.

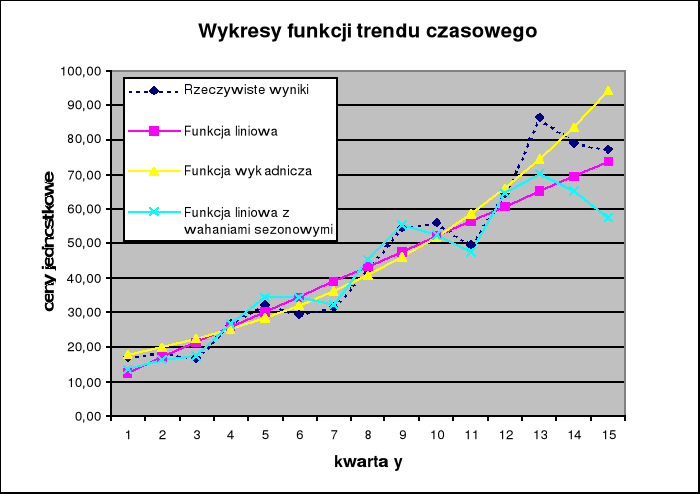
Rysunek 3 (wykres cen gruntów oraz prognozy cen uzyskane dla poszczególnych funkcji):

Z jednej strony można powiedzieć, że w dużej mierze prognoza okazała się trafna. Obserwując powyższy rysunek widać, że zarówno wykres funkcji liniowej jak i wykładniczej charakteryzują się dość dobrą zbieżnością z wynikami obserwacji. Z drugiej strony oczekiwany był znacznie lepszy wynik, zwłaszcza jeśli chodzi o wariant funkcji liniowej z uwzględnionymi wahaniami sezonowymi. Wytłumaczeniem tego stanu rzeczy mogą być następujące przyczyny:

1. Nieruchomości, a zwłaszcza nieruchomości gruntowe zlokalizowane na bardzo intratnych terenach, charakteryzują się tak dużą atrakcyjnością dla potencjalnych nabywców, że ich stały wzrost wartości jest niejako pewny, zaś zinterpretowane jako wahania sezonowe spadki cen, były wynikiem innych czynników niż zmiany w układzie sił podaży i popytu. Należy przy tym zauważyć, że w niektórych kwartałach ilość transakcji była tak niewielka, że mogło to mieć wpływ na zniekształcenie obserwowanych zależności.

2. Na ceny transakcyjne nieruchomości gruntowych, które były przedmiotem analizy, wpływa tak wiele czynników, że błędem jest wyciąganie dalece idących wniosków co do trendu czasowego, jak np. wahania sezonowe. Inaczej mówiąc, jeśli nawet wahania sezonowe miały miejsce, to ilość różnorodnych czynników wpływających na ceny jest na tyle, że brak jest możliwości wychwycenia cyklicznych tendencji. Analizę należy zatem zakończyć na wyznaczeniu funkcji liniowej (lub wykładniczej).

3. Pomysł wyznaczenia i uwzględnienia wahań sezonowych był poprawny (co częściowo udowodniły uzyskane wyniki), za krótki okazał się jednak badany okres. Poprawnym działaniem jest zatem ponowne wyznaczenie funkcji liniowej z uwzględnionymi wahaniami sezonowymi, w oparciu o dane z okresu II kwartał 1995 - I kwartał 1999 roku.

4. Funkcje trendu czasowego (w tym funkcja liniowa z uwzględnieniem wahań sezonowych) zostały poprawnie określone, natomiast pod koniec 1998 roku (III i IV kwartał) mogła mieć miejsce na rynku nieruchomości taka sytuacja, która spowodowała znacznie zwiększony popyt na nieruchomości. Spowodowało to czasowy wzrost cen nieruchomości ponad prognozowaną wielkość. W roku 1999 sytuacja na rynku nieruchomości wróciła do normy, co obrazuje m.in. zbieżność cen transakcyjnych do wyniku uzyskanego przy użyciu funkcji liniowej.

Aby odpowiedzieć na pytanie która z ww. sytuacji (lub ich kombinacja) miała miejsce należy przeprowadzić dalsze badania. Dopiero one bowiem mogą dać odpowiedź na pytanie jak prawidłowo wyznaczać funkcje wzrostu cen nieruchomości oraz w jaki sposób dokonywać prognoz zmian cen w dającej się przewidzieć przyszłości. Nie jest to tematem niniejszego opracowania. Ponieważ jednak dostępne dane pozwalają na ponowne wyznaczenie funkcji trendu w oparciu o obserwowanych 15 okresów (w odróżnieniu od części 1 artykułu gdzie analizy dokonano w oparciu o dane z 12 kwartałów) autor zdecydował się na ponowne wyznaczenie funkcji regresji. W wyniku obliczeń dokonanych dla poszerzonej grupy danych uzyskano następujące wyniki:

Lp.	Funkcja regresji	Stała M	Stała B	Wsp. korelacji
1.	liniowa	5,05	5,12	0,96
2.	wykładnicza	0,11	17,05	0,96

Autor opracowania dokonał ponadto wyznaczenia funkcji regresji liniowej z uwzględnionymi wahaniami sezono-wymi (analogicznie jak w części pierwszej artykułu).

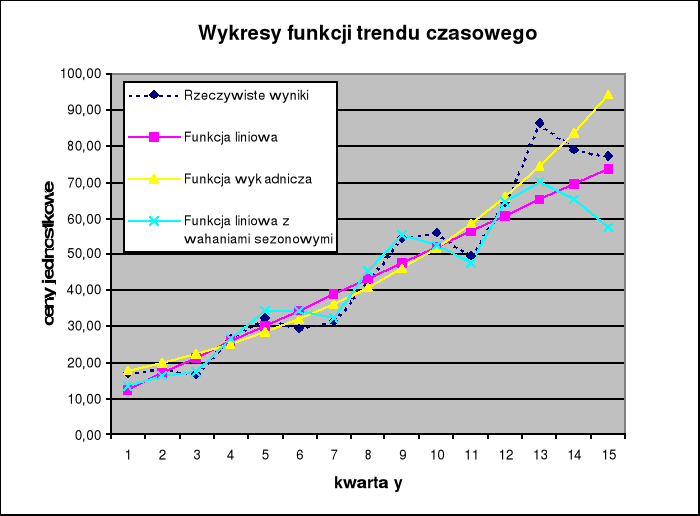
Rysunek 4 (wykres rzeczywistych cen gruntów oraz nowo wyznaczonych funkcji regresji):

Literatura:

[1] J. Jóźwiak, J. Podgórski „Statystyka od podstaw”; Polskie Wydawnictwo Ekonomiczne, Warszawa 1997 r.

[2] M. Sobczyk „Statystyka”; Wydawnictwo Naukowe PWN, Warszawa 1994 r.

[3] A. Stanisz „Przystępny kurs statystyki”; Wydawnictwo StatSoft Polska Sp. z o.o., Kraków 1998 r.

---