Politechnika Częstochowska

Instytut Fizyki

Ćwiczenie nr 14

Temat: Pomiar pojemności kondensatora metodą rozładowania

Tadeusz Mariański

Rafał Młyńczak

Informatyka

Rok II

Grupa V

Pojemnością elektryczną C nazywamy iloraz ładunku Q zgromadzonego na okładkach kondensatora i napięcia U_w panującego między jego okładkami:

C =

Kiedy podstawimy na napięcie U_w potencjał względny równy E =
(gdzie d jest odległością płytki dodatniej, a na Q=δ S (gdzie δ jest gęstością powierzchniową ładunku, a S powierzchnią płytek, otrzymamy wzór

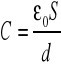
Gdy uwzględnimy środowisko o względnej przenikalności dielektrycznej między okładkami oznaczane przez ε_r otrzymamy wzór:

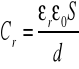
Jak widać pojemność kondensatora jest wprost proporcjonalna do powierzchni jego płytek, a odwrotnie proporcjonalna do ich odległości. Pojemność jest również zależna od przestrzeni między okładkami.

Łączenie kondensatorów

Istnieją dwie możliwości łączenia kondensatorów: Równoległe i szeregowe.

Z Połączeniem szeregowym mamy do czynienia gdy na pierwszą okładkę połączoną z biegunem dodatnim wprowadzamy ładunek +Q, ostatnią zaś łączymy z biegunem źródła o potencjale V_n+1. Na pozostałych okładkach tworzą się przez indukcję ładunki odpowiednio -Q i +Q. Napięcia między poszczególnymi okładkami będą równe V₁-V₂=Q/C₁ dla pary pierwszej, V₂-V₃=Q/C₂ dla pary drugiej, zaś dla pary n-tej V_n-V_n+1=Q/C_n Otrzymujemy wzór

V₁-V_n+1=Q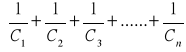

gdzie V₁ -V_n+1=U - napięcie przyłożone między okładką pierwszą i ostatnią.

Porównując wzór z zasadniczym wzorem można zauważyć, że odwrotność pojemności układu złożonego z kondensatorów połączonych szeregowo jest równa sumie odwrotności poszczególnych kondensatorów:

Schemat połączenia szeregowego kondensatorów:

Łączenie równoległe kondensatorów polega jak sama nazwa wskazuje na połączeniu przewodnikiem okładek równolegle, jak na rysunku poniżej. Powstaje wtedy nowy układ o większej powierzchni okładek. Wszystkie połączone z biegunem dodatnim mają potencjał V₁, a wszystkie połączone z biegunem ujemnym źródła mają potencjał V₂. Napięcie między okładkami każdego z kondensatorów składowych jest równe U. Ładunki przypadające na poszczególne kondensatory można wyrazić wzorem Q_n = C_nU gdzie n jest odpowiednią liczbą odpowiadającą numerowi kondensatora. Kiedy wszystko zsumujemy otrzymamy: Q₁+Q₂+Q₃+...+Q_n=(C₁+C₂+C₃+.......+C_n)U

Układ równolegle połączonych kondensatorów ma pojemność równą sumie

pojemności kondensatorów składowych:

C= C₁+C₂+C₃+.......+C_n =

Schemat połączenia równoległego kondensatorów:

Ładowanie i rozładowywanie kondensatora

Wprowadzając dodatkowy ładunek dQ spowodujemy wzrost napięcia o dU i równanie Q=CU będzie mieć postać: Q + dQ = C(U+dU)

Po przekształceniu otrzymamy: CdU=dQ, C=dQ/dU (1)

Przy założeniu, że kondensator na którego okładkach panuje napięcie U₀ rozładowujemy przez opór R. wtedy ubytek ładunku zgodnie z definicja (dQ=Idt) wynosi -dQ=Idt, a ponadto zgodnie z prawem Ohma mamy: dU=RdI

Podstawiając ostatnie dwa związki do równania (1) otrzymamy RcdI=-Idt

Porządkując powyższe wyrażenie i całkując w granicach od 0 do t otrzymamy:

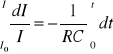
Po scałkowaniu równość przyjmuje postać

lub

W przypadku ładowania kondensatora wzór powyższy przyjmuje postać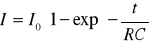

Podstawiając za I i I₀ do równania powyższego otrzymamy wzory, którymi wyraża się spadek napięcia przy rozładowaniu

lub przy ładowaniu kondensatora

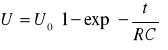
Schemat układu pomiarowego :

---