W równaniach opisujących ładowanie i rozładowanie kondensatora wielkość RC ma wymiar czasu i jest nazywana stałą czasową obwodu. Opisuje ona fakt, że ładunek na kondensatorze nie osiąga od razu wartości końcowej lecz zbliża się do niej wykładniczo. Podobnie przy rozładowaniu.
Rysunek 1. przedstawia schemat badanego obwodu RC. W trakcie ładowania kondensatora podłączonego do
źródła napięcia stałego poprzez szeregowo włączony opornik natężenie prądu w obwodzie, napięcie i ładunek na
kondensatorze ulegają zmianom w czasie. Początkowo kondensator jest nienaładowany i zamknięcie obwodu w chwili
t = 0 wywołuje przepływ prądu ładującego go. Początkowa wartość napięcia na kondensatorze wynosi UC = 0, spadek
potencjału na oporniku jest równy napięciu źródła a prąd początkowy - i0. W trakcie ładowania kondensatora napięcie
na jego okładkach rośnie a różnica potencjałów na oporniku maleje, odpowiednio do malejącego natężenia prądu w
obwodzie. Po pewnym czasie kondensator zostaje prawie całkowicie naładowany, prąd spada do zera podobnie jak
napięcie na oporniku. Różnica potencjałów na okładkach kondensatora jest równa napięciu pomiędzy zaciskami źródła.
Jeżeli w obwodzie znajduje się wyłącznie opornik o oporności (oporze
omowym) R, do którego przyłożono stałe napięcie U, to natężenie prądu I
płynącego przez ten opornik jest proporcjonalne do przyłożonego napięcia
gdzie jest amplitudą napięcia na oporniku. Zauważmy, że nie ma
przesunięcia fazowego między prądem a napięciem. Innymi słowy, napięcie na
oporniku jest w każdej chwili proporcjonalne do natężenia płynącego prądu.
U I R0 0 = R
Jeżeli obwód prądu zmiennego,
oprócz opornika, zawiera także
cewkę i kondensator, jak to
przedstawiono na rys. 53.1., to mamy
do czynienia również z oporem
indukcyjnym cewki X L i oporem
pojemnościowym kon-densatora
XC . Jeżeli prąd płynący przez
cewkę dany jest wzorem (53.2), to
powstaje w niej siła elektromotoryna
samoindukcji ( ) ĺ
s L dI dt = - / ,
gdzie L indukcyjność cewki. Stąd
napięcie UL na cewce
cz
I0
Zatem amplituda napięcia na cewce wynosi U L L0 = ů . Związek ten ma
podobną postać jak w przypadku opornika, z tą różnicą, że zamiast R
występuje w nim wielkość ů , nazywana opornością indukcyjną cewki L
X L L = ů . (53.5)
Poza tym napięcie UL wyprzedza w fazie natężenie prądu I o kąt równy
czyli o ćwierć okresu.
đ/ 2
Elementem obwodu prądu zmiennego może być również kondensator.
W dowolnej chwili napięcie na kondensatorze UC wiąże się z chwilową
wartością ładunku q na okładkach kondensatora zależnością q CUC
= , gdzie C
jest pojemnością kondensatora. Szybkość zmiany ładunku q jest równa
natężeniu prądu w obwodzie
Napięcie na kondensatorze jest, podobnie jak napięcie na cewce,
przesunięte w fazie względem natężenia prądu, przy czym przesunięcie fazy
wynosi teraz - đ/ 2
/ 2
. Oznacza to, że napięcie opóźnia się w fazie
względem prądu o đ , czyli o ćwierć okresu.
UC
Obliczmy teraz napięcie U U U U R L C = + + na całym obwodzie
uwzględniając przesunięcia fazowe napięć na cewce i kondensatorze. Jeżeli
napięcia , i U są harmonicznymi funkcjami czasu, to również
napięcie U jest funkcją harmoniczną i ma postać
UR UL C
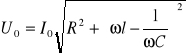
Jeżeli amplituda napięcia jest stała, a zmienia się częstość U0 ů,
następuje gwałtowny wzrost prądu, gdy częstość dąży do częstości
rezonansowej (patrz ćwiczenie 54).
Wyszukiwarka
Podobne podstrony:
obwód RC, mechanika, BIEM- POMOCE, laborki elektra
wnoski RLc, mechanika, BIEM- POMOCE, laborki elektra
obwód równoległy RLC, mechanika, BIEM- POMOCE, laborki elektra
układy elektroniczne-laborka, mechanika, BIEM- POMOCE, laborki elektra
omomierze, mechanika, BIEM- POMOCE, laborki elektra
RLC równoległy, mechanika, BIEM- POMOCE, laborki elektra
dioda prostownicza, mechanika, BIEM- POMOCE, laborki elektra
rez row, mechanika, BIEM- POMOCE, laborki elektra
przygotowanie do stanowiska, mechanika, BIEM- POMOCE, laborki elektra
dioda Zenera, mechanika, BIEM- POMOCE, laborki elektra
E12, mechanika, BIEM- POMOCE, laborki elektra
prawa ohma, mechanika, BIEM- POMOCE, laborki elektra
prad sin, mechanika, BIEM- POMOCE, laborki elektra
PRZYRZDY CYFROWE, mechanika, BIEM- POMOCE, laborki elektra
Pytania+z+elektrotechniki, mechanika, BIEM- POMOCE, laborki elektra
tranzystor sprawozdanie, mechanika, BIEM- POMOCE, laborki elektra
więcej podobnych podstron