Zestaw 6

1. Energia całkowita ciała drgającego poruszającego się ruchem harmonicznym jest równa 3*10^-5J, a maksymalna siła działająca na ciało 1.5*10^-3N. Napisać równanie ruchu tego ciała f=x(t), skoro okres drgań wynosi 2s, a faza początkowa wynosi równa 60^o.

2. Sprężyna o zaniedbywalnej masie i współczynniku sprężystości 19 N/m wisi w pozycji pionowej. Do jej wolnego końca przymocowano ciało o masie 0,20 kg, które puszczono w chwili gdy sprężyna znajdowała się w stanie nierozciągniętym. Znaleźć maksymalną odległość od początkowego położenia, na którą przemieści się ciało oraz częstość i amplitudę ruchu harmonicznego w jaki zostanie wprawione ciało. Powtórzyć obliczenia dla sprężyny, która powstała z przecięcia sprężyny wyjściowej na dwie równe części.

3. Dwie sprężyny o współczynnikach sprężystości k₁ i k₂ przymocowano do ciała o masie m tak jak pokazano na rysunkach a) i b). Ciało porusza się po powierzchni bez tarcia. Pokazać, że częstość kołowa drgań w przypadku a) i b) jest równa odpowiednio:

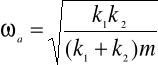
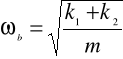
4. Przez kule ziemską przewiercono tunel wzdłuż średnicy. Pokazać, że ciało wrzucone do tunelu będzie się poruszać ruchem harmonicznym. Obliczyć częstość drgań, zakładając, że nie ma sił oporu.

5. Klocek o masie 8 kg zawieszono na sprężynie o współczynniku sprężystości k=30 N/m. Z dołu w kierunku klocka wystrzelono z prędkością 500 m/s pocisk o masie 0.1 kg, który utknął w klocku. Znaleźć amplitudę ruchu harmonicznego w jaki został wprawiony klocek. Jaka część energii kinetycznej pocisku została zmagazynowana w oscylatorze harmonicznym. Co się stało z resztą energii?

6. Ciało znajduje się na poziomej powierzchni, która porusza się poziomo prostym ruchem harmonicznym z częstotliwością dwóch drgań na sekundę. Współczynnik tarcia statycznego między ciałem, a tą powierzchnią wynosi µ_s = 1. Jak duża może być amplituda tego ruchu, aby ciało nie ślizgało się po powierzchni?

7. Energia potencjalna, odpowiadająca pewnemu dwuwymiarowemu polu sił wyraża się wzorem:

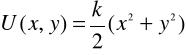
Opisać wektorowo to pole sił i zaproponować jego fizyczny model. Pokazać, że rozwiązaniem ruch pod wpływem takiej siły jest złożenie dwóch prostopadłych drgań harmonicznych. Dla jakich wartości amplitud i faz drgań składowych trzymujemy równanie koła, elipsy symetrycznej względem osi x lub y, elipsy symetrycznej względem prostej x=y, równanie prostej y=ax.

8. Oblicz jaki jest współczynnik tłumienia β ruchu harmonicznego jeżeli jego amplituda maleje dwukrotnie w czasie t = 1 min. Ile razy zmalała w tym czasie energia drgań?

k₁

k₂

m

m

a)

k₂

k₁

b)

---