WFiTJ	Imię i Nazwisko: 1. Łukasz Wędel 2. Jędrzej Donizak		ROK II	GRUPA	ZESPÓŁ
Pracownia Fizyczna II	Temat: Dyfrakcja światła na szczelinie				Nr ćwiczenia: 71
Data wykonania:	Data oddania:	Zwrot do poprawy:	Data oddania:	Data zaliczenia:	OCENA

1. Cel ćwiczenia.

Zjawisko dyfrakcji - czyli uginania promieni traktujemy jako nakładanie się fal cząstkowych pochodzących z ciągłego rozkładu spójnych źródeł. Jest to superpozycja nieskończonej liczby przyczynków fal pochodzących od punktów szczeliny, z których każdy jest źródłem fali kulistej nie wstecznej (zasada Huygensa).

Zjawisko to możemy obserwować w łatwy sposób - oświetlając wąską, pojedynczą szczelinę równoległą wiązką światła laserowego. Przyjmujemy, że laser emituje światło monochromatyczne o długości fali λ. Na ekranie ustawionym w dużej odległości L od szczeliny ( L>>λ ) obserwujemy obraz dyfrakcyjny, do rozważań którego można zastosować przybliżenie Fraunhoffera .

Obrazem dyfrakcyjnym nazywamy rozkład natężenia oświetlenia po przejściu przez strukturę uginającą. Skalarny opis dyfrakcji bez uwzględniania polaryzacji fali elektromagnetycznej jest wystarczająco dokładny, jeśli wielkość elementów struktury uginającej oraz odległości pomiędzy ekranem i przeszkodą są dostatecznie duże w porównaniu z długością fali.

W typowym doświadczeniu z dyfrakcja światła rozmiary szczeliny są rzędu ułamka milimetra, czyli 103 razy większe od długości fali światła widzialnego ( założenie jest więc zawsze spełnione). Z drugiej strony odległości źródło - szczelina i szczelina - ekran są rzędu metra, 103 razy większe od szerokości szczeliny. Wystarczy zatem opis podany przez Fraunhoffera. W tym opisie powierzchnie falowe są płaszczyznami, co sprawia, że rozkład natężenia w obrazie dyfrakcyjnym może być opisany za pomocą wzorów analitycznych.

Rozkład natężenia światła na ekranie w dyfrakcji na pojedynczej szczelinie określa wzór:

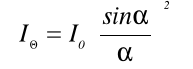
(1)

gdzie:

Wymiary geometryczne a, x, l, są przedstawione na rysunku:

- kąt ugięcia.

Io - natężenie światła dla maksimum, centralnego.

a- szerokość szczeliny

= ϕ/2 gdzie: ϕ - różnica faz pomiędzy promieniami pochodzącymi z dwóch krańców szczeliny .

Dla kąta θ = 0 otrzymamy maksimum natężenia światła; szerokość tego maksimum rośnie przy zwężaniu szczeliny. Ze wzoru (1) otrzymujemy ogólne wyrażenie dla minimum natężenia obrazu dyfrakcyjnego w funkcji kąta ugięcia θ .

gdzie n = 1, 2,3, ...

Pomiędzy każdą parą sąsiednich minimów znajdują się maksima natężenia światła, dla których spełniony jest warunek :

gdzie m= 1,2,3,...

Dla małych kątów θ można stosowa przybliżenie:

sinθ = tgθ = y/L

gdzie:

L- odległość szczeliny od ekranu,

y - współrzędna odpowiadająca kątowi θ (załączony rysunek schematu pomiarowego)

Ostatecznie dla n=1 otrzymujemy wyrażenie na szerokość szczeliny :

(2)

gdzie:

y_min¹ - położenie pierwszego minimum rozkładu natężenia światła w obrazie dyfrakcyjnym

Możemy też zapisać wzór ogólny dla n- tego minimum zastępując y_min¹ czynnikiem y_minⁿ dla n=1,2,3,...

Oraz wzór ogólny dla m- tego maksimum:

gdzie m= 1,2,3,...

Uwzględniając sąsiadujące maksima i minima:

(3)

gdzie Y_i jest zdefiniowane następująco :

Y_i = 0,5(y_max^m - y_minⁿ ) (maksimum główne)

Y_i = y_max^m - y_minⁿ (maksimum poboczne)

Zjawisko dyfrakcji ogranicza zdolność rozdzielczą wszystkich instrumentów optycznych. Kryterium Rayleigh`a określa, że jeżeli na pojedynczą szczelinę o szerokości a pada światło z dwóch oddzielnych, identycznych źródeł rozdzielonych kątowo, ich obrazy dyfrakcyjne można uznać za rozdzielone gdy odległość pomiędzy głównymi maksimami jest większa niż pierwszego minimum od odpowiadającego mu maksimum głównego. Warunek ten jest spełniony, jeżeli minimalna odległość kątowa θ_min pomiędzy tymi źródłami wynosi : θ_min = λ/a

W skład naszego zestawu pomiarowego wchodzą elementy zamocowane na ławie optycznej. (Rysunek schematyczny zamieszczony na następnej stronie.)

Dioda laserowa znajduje się wewnątrz szczelnej obudowy, jest spolaryzowana w kierunku przewodzenia i ma rozmiary nie przekraczające 1mm. Warstwa czynna lasera , z której emitowane jest światło ma szerokość 2-10 μm. Emitowane przez diodę laserową światło jest skierowane na układ optyczny formujący szeroką, równoległą wiązkę. Wiązka światła jest skierowana na poziomo ustawioną szczelinę o szerokości regulowanej. Ugięcie światła obserwujemy na ekranie ustawionym prostopadle do wiązki promieniowania z lasera. W płaszczyźnie równoległej do ekranu możemy ustawić fotodiodę. Położenie fotodiody ustawiamy w osi x z dokładnością nie przekraczającą 0,5 mm oraz w osi z dokładnością do 0,05 mm.

2. Wyniki pomiarów i ich opracowanie.

Pojedyncza szczelina

Obliczam szerokość szczeliny d (pojedyncza szczelina).

Korzystamy ze wzorów:

(1) Y_i = 0,5(y_max^m - y_minⁿ ) (maksimum główne)

(2) Y_i = y_max^m - y_minⁿ (maksimum poboczne)

Dla maksimum głównego i pierwszych minimów uzyskujemy:

Y₁ = |0,5(15,855-15,985)| = 0,065 mm

Y₂ = |0,5(15,855-15,725| = 0,065 mm

Dla 1-szych maksimów pobocznych i 2-gich minimów uzyskujemy:

Y₃ = |16,015-16,095| = 0,08 mm

Y₄ = |15,695-15,615| = 0,08 mm

Dla 2-gich maksimów pobocznych i 3-gich minimów uzyskujemy:

Y₅ = |16,015-16,095| = 0,08 mm

Y₆ = |15,575-15,495| = 0,08 mm

= (0,065 + 0,065 + 0,08 + 0,08 + 0,08 + 0,08)/6 = 0,075 mm

= 0,008 mm (Obliczone z rozkładu studenta za pomocą programu MS Excel)

Wyliczam d:

Obliczam niepewność d

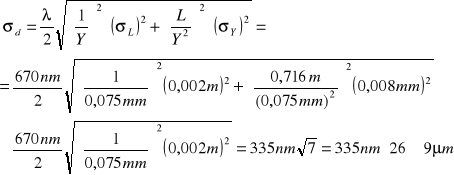
3. Wnioski.

Z obliczeń wynika, że szczelina ma szerokość 64(9) μm. Szerokość teoretyczna odczytana podczas wykonywania doświadczenia wynosi 90 μm. Wynik teoretyczny mieści się w 3σ wyliczonej wartości.

Wykres dla 1 szczeliny całkowicie zgadza się z przewidywaniami teoretycznymi.

Z powodu braku czasu nie wykonaliśmy pomiarów dla podwójnej szczeliny.

Doświadczenie pozwoliło nam praktycznie zaobserwować dyfrakcję światła na szczelinie.

5

---