GRUPA 10

Joanna Łużna

Magdalena Matłaszek

Ćwiczenie nr 32 MOSTEK Wheatstone'a

1.Wstęp teoretyczny:

Prąd elektryczny

Jest to każdy uporządkowany (skierowany) ruch ładunków elektrycznych.

Natężenie prądu

Wielkość opisująca prąd elektryczny.

Jest pochodną ładunku elektrycznego q, który przepływa przez poprzeczny przekrój przewodnika, po czasie t przepływu tego ładunku.

Można je tez wyrazić za pomocą wzoru:

gdzie:

I - natężenie prądu

n - koncentracja nośników prądu wyrażona przez ich liczbę na jednostkę objętości (poruszających się w tym samym kierunku)

q - ładunek każdego z nośników

V - objętość

s - przekrój poprzeczny

Amper

Jednostka natężenia prądu.

Natężenie prądu płynącego w przewodniku jest ilością przepływającego ładunku w jednostce czasu.

Amper jest jednostką podstawową w układzie SI. Przy jego pomocy definiuje się kolumba(jednostka pochodna).

Amper absolutny(definicja):

Stały prąd elektryczny, który płynąc w dwóch równoległych, prostoliniowych, nieskończenie długich przewodach o znikomo małym przekroju kołowym, umieszczonych w próżni w odległości 1m od siebie, spowodowałby wzajemne oddziaływanie przewodów na siebie z siłą równą F=2

N na każdy metr długości przewodu.

Napięcie:

Jest różnicą potencjałów elektrycznych między dwoma punktami obwodu elektrycznego lub pola elektrycznego.

gdzie:

- napięcie miedzy dwoma punktami

- różnica potencjałów miedzy punktami a i b

-praca wykonana podczas przenoszenia ładunku punktu a do b

q- ładunek

Napięcie elektryczne to stosunek pracy wykonanej podczas przenoszenia ładunku między punktami, dla których określa się napięcie, do wartości tego ładunku.

Wolt

Jednostka potencjału elektrycznego, czyli pracy potrzebnej do przeniesienia ładunku punktowego z punktu a do punktu b w polu elektrycznym.

Opór

Inaczej rezystancja lub oporność.

Jest miarą oporu czynnego, z jakim element przeciwstawia się przepływowi prądu elektrycznego.

gdzie:

R- opór

-opór właściwy(wielkość charakterystyczna dla danej substancji)

l - długość przewodnika w którym płynie prąd

s - przekrój poprzeczny przewodnika

Prawo Ohma:

gdzie:

R - opór

U - napięcie

I - natężenie

Jednostką rezystancji w układzie SI jest om(1 Ω).

I prawo Kirchoffa

Suma natężeń prądów wpływających do węzła jest równa sumie natężeń prądów wypływających z tego węzła.

II. Prawo Kirchoffa

W obwodzie zamkniętym suma spadków napięć na wszystkich odbiornikach prądu musi być równa sumie napięć na źródłach napięcia.

Drugie prawo Kirchhoffa jest uzupełnieniem pierwszego prawa Kirchhoffa.

Oba te prawa łącznie pozwalają na tzw.”Rozwiązywanie obwodów”, czyli na obliczaniu natężeń prądów płynących w różnych gałęziach obwodu, dzięki znajomości oporów i sił elektromotorycznych źródeł.

2.Cel doświadczenia:

Celem tego doświadczenia było wyznaczenie oporu zastępczego połączonych oporników tak, by równoważył on opór zadany, a przez środkową gałąź obwodu nie płynął prąd.

3.Wykonanie doświadczenia:

1)połączenie obwodu elektrycznego wg schematu (rys):

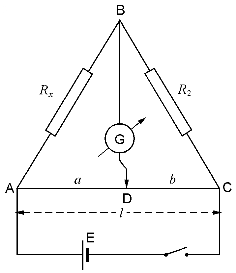
2) pomiar oporu dla opornika
, przy zadanym natężeniu prądu wahającym się w niewielkim stopniu w okolicach
(dla takich wartości układ wykazuje odpowiednią czułość na zmiany oporu), (opór obliczany ze wzoru
);

3) pomiar oporu dla opornika
,

4) pomiar oporu dla połączenia szeregowego oporników
i
;

5) pomiar oporu dla połączenia równoległego tych samych oporników.

4. Wyniki pomiarowe:

Tabela 1								Długość drutu lo: 100 [cm]
Opór wzorcowy []	12	13	14	15	16	15	11		10	9	13
a [cm]	50,5	48,5	46,7	45	43,3	45	52,8		55,3	58	48,5
[]	12,24	12,24	12,27	12,27	12,22	12,27	12,31		12,37	12,43	12,243
u( ) []	0,12	0,10	0,10	0,010	0,09	0,10	0,13		0,14	0,15	0,109

Tabela 2								Długość drutu lo: 100 [cm]
Opór wzorcowy []	24	26	25	24	23	27	30		32	34	36
a [cm]	58,5	56,5	57,4	58,4	59,6	55,6	52,8		51,3	49,7	48,2
[]	33,83	33,77	33,69	33,69	33,81	33,81	33,56		33,98	33,59	33,50
u( ) []	0,2	0,2	0,2	0,2	0,2	0,2	0,19		0,18	0,18	0,18

Tabela 3 POŁĄCZENIE SZEREGOWE								Długość drutu lo: 100 [cm]
Opór wzorcowy []	48	46	44	42	40	45	47		49	51	53
a [cm]	49	50	51,1	52,4	53,6	50,5	49,4		48,3	47,3	46,4
, []	46,12	46,00	45,98	46,24	46,21	45,91	45,89		45,78	45,77	45,88
[]	0,03	0,03	0,03	0,03	0,03	0,03	0,03		0,03	0,03	0,03

Tabela 4 POŁĄCZENIE RÓWNOLEGŁE								Długość drutu lo: 100 [cm]
Opór wzorcowy []	10	11	12	13	9	8	7		6	14	11
a [cm]	47,2	44,9	42,7	40,9	50,2	53,1	56,5		60,4	38,9	44,9
, []	8,94	8,96	8,94	9,00	9,07	9,06	9,09		9,08	8,91	8,96
[]	0,0013	0,0013	0,0013	0,0014	0,0013	0,0013	0,0013		0,0014	0,0014	0,0013

5. Opracowanie wyników pomiarów:

Wartości średnie dla poszczególnych oporów i ich niepewności:

12,2863[]

(z prawa przenoszenia wg wzoru:
):

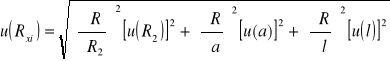
- zamieszczone w tabeli;

średnia wartość: 0,0114[]

33,723
33,7 []

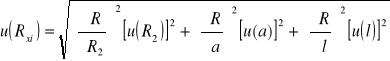
- zamieszczone w tabeli;

średnia wartość: 0,19904175
0,2[]

Dla połączenia szeregowego:

= 45,976
45,98[]

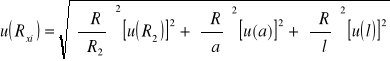
- zamieszczone w tabeli;

wartość średnia niepewności: 0,03[]

Dla połączenia równoległego:

= 9,0016[]

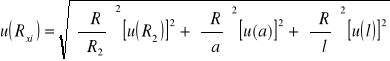
- zamieszczone w tabeli;

wartość średnia niepewności: 0,00135117
0,0014[]

Obliczenie oporów zastępczych (ze wzorów) i ich niepewności (z prawa przenoszenia):

Dla połączenia szeregowego:

=
+
12,286 + 33,7 = 45,986
46,0[]

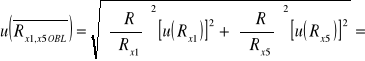
0,229286194
0,2[]

Dla połączenia równoległego:

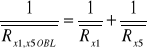
= 9,01[]

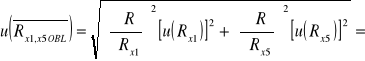
0,062772
0,06 []

Obliczenie błędu systematycznego:

(dla poł.szer.)-
=46,02115-45,9764=
0,04475

0,04[]

Jest to zbyt duża liczba jak na błąd systematyczny, dlatego pomijamy dwa pomiary, które najbardziej różnią się od całości (zaznaczone na żółto w tabeli) i wykonujemy ponowne obliczenia:

Tabela 3 POŁĄCZENIE SZEREGOWE								Długość drutu lo: 100 [cm]
Opór wzorcowy []	48	46	44	42	40	45	47		49	51	53
a [cm]	49	50	51,1	52,4	53,6	50,5	49,4		48,3	47,3	46,4
, []	46,12	46,00	45,98	46,24	46,21	45,91	45,89		45,78	45,77	45,88
[]	0,03	0,03	0,03	0,03	0,03	0,03	0,03		0,03	0,03	0,03

Wartości średnie dla poszczególnych oporów i ich niepewności (z pominięciem dwóch wyników):

Dla połączenia szeregowego:

= 46,027
46,03[]

0,03[]

=46,0[]

Błąd systematyczny:

-
=
0,03Ω

Podsumowanie wyników:

Tabela 5
Opór średni dla połączenia szeregowego (niepewność)	46,03[] (0,03[])	Opór zastępczy dla połączenia szeregowego (niepewność)	46,0[] (0,2[])
Opór średni dla połączenia równoległego (niepewność)	9,0016[] (0,0014[])	Opór zastępczy dla połączenia równoległego (niepewność)	9,01[] (0,06 [])

7.Wnioski:

Doświadczenie pozwoliło nam wyznaczyć nieznane opory R_x1 i R_x5 oraz potwierdziło wzory na opór zastępczy przy łączeniu szeregowym i równoległym.

Mostek Wheatstone'a jest dokładnym układem do pomiaru nieznanych rezystencji.

W tdwuch przypadkach uzyskane niepewności dla dokonanych pomiarów są bardzo małe, jednak niepewność obliczona dla połączenia szeregowego i równoległego znacznie przewyższa pozostałe wielkości(niepewność dla szeregowego jest rzędu 0,4% a dla równoległego na poziomie 0,7% jednak przy użyciu stoswanego w doświadczeniu mostka powinnyśmy użyskać mniejszą niepewność).

Prawdopodobną przyczyną tych rozbierzności z oczekiwaniami mógł być błąd ludzki lub aparatura do pomiarowa, która mogła być na tyle niedokładna, aby zaburzyć wyniki doświadczenia .

Przez cały czas trwania doświadczenia natężenie prądu płynącego w obwodzie było stałę i wynosiło 0,5 A.

Wykonywane przez nas doświadczenie pozwoliło nam zapoznać się z nieznanymi do tej pory z praktyki elementami obwodu elektrycznego oraz technikami jego mantażu.

---