nr æw. 109	data 22.05.03	Tomasz Żmuda	Wydział MRiT	Semestr IV	grupa T6
prowadzący : dr J.Ruczkowski			przygotowanie	wykonanie	ocena końcowa

Badanie Ruchu jednostajnie zmiennego

Wprowadzenie:

By przejść do badania ruchu jednostajnie zmiennego należy zapoznać się z kinematyką.

Oto podstawowe wzory, które będą później potrzebne.

W ruchu jednostajnie zmiennym drogę przebytą można wyrazić wzorem:

S=0,5*a*t²+t*V₀+S₀

Ciekawe efekty wywołuje również siła tarcia. Będziemy ją badać za pomocą równi pochyłej.

W tym przypadku tarcie można wyrazić wzorem:

T=m_w*g*sin(a)-m_p*g-a(m_w+m_p):

Gdzie:

m_p, m_w - masa przeciwwagi i wózka

a - przyspieszenie wózka jakie wyznaczymy

Obliczenia:

T=m_w*g*sin()-(m_p*g)-a(m_w+m_p)

gdzie:

 - kąt nachylenia równi pochyłej

m_p, m_w - masa przeciwwagi i wózka

a - przyspieszenie wózka jakie wyznaczymy

Wynik dla danej serii pomiarów został wyliczony ze średniej arytmetycznej poszczególnych pomiarów. Obliczyłem także odchylenie standardowe.

Wyznaczanie siły tarcia dla wózka
1 Seria			W. Obl	inne dane
L.p	a	T		Kąt A	25
1	1,01945	0,01131	T śr	mw [kg]	0,35
2	1,03309	0,00517	0,00201	mp [kg]	0,1
3	1,06779	-0,0104	Odch St T
			0,011215
2 Seria			W. Obl	inne dane
L.p	a	T		Kąt A	20
1	0,42283	0,00305	T śr	mw [kg]	0,35
2	0,38796	0,01874	0,011352	mp [kg]	0,1
3	0,40237	0,01226	Odch st T
			0,007885
3 Seria			W. obl	inne dane
L.p	a	T		Kąt A	15
1	0,054374	0,00742	T śr	mw [kg]	0,4
2	0,07246	-0,0016	0,000344	mp [kg]	0,1
3	0,07874	-0,0048	Odch st T
			0,006325
4 Seria			W. Obl	inne dane
L.p	a	T		Kąt A	10
1	0,17686	0,0026	T śr	mw [kg]	0,44
2	0,17238	0,00487	0,004581	mp [kg]	0,067
3	0,1696	0,00628	Odch St T
			0,001857

Wydruk z arkusza kalkulacyjnego:

Wyznaczanie przyspieszenia
ziemskiego
L.p.	g
1	9,7376
2	9,6928
3	9,8095
4	9,6978
Średnia ar		9,733367
odch. Standardowe		0,065981

Dyskusja Błędu:

Trudno jest mi określić dokładność pomiarową przyrządów. Podawały one już wyniki częściowo przeliczone. Niestety nie miałem takich informacji jak na przykład dokładność masy wózka, czy masa przeciwwagi. W doświadczeniu A komputer podawał tylko gotowe wyniki. Nie pokazywał wartości dt (czasu w którym następny szczebel drabinki zasłaniał fotokomórkę). Granice błędu policzyłem z odchylenia standardowego.

Dla doświadczenia A można było wyrazić je wzorem

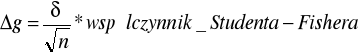
Uwzględnianie współczynnika Studenta-Fishera jest konieczne, dla n = 4 równy 1,3.

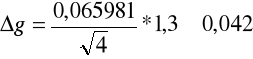
Zatem na końcu doświadczenia uzyskałem wynik :

W doświadczeniu B średnia arytmetyczna była obliczona z 3. Zatem dodatkowo uwzględniłem jeszcze współczynnik Studenta-Fishera.

Dla 3 pomiarów miał on wartość 1,4 .

Więc granicę błędu można wyrazić wzorem:

Na końcu uzyskałem wyniki:

Seria	Tarcie [N]	Granica błędu [N]:
1	0,002	0,009
2	0,011	0,006
3	-0,002	0,005
4	0,004	0,001

Wnioski:

Doświadczenie A pozwoliło na wyznaczenie przyspieszenia ziemskiego z dużą dokładnością. Główną zasługę odegrał w tym komputer. Mógł on bardzo precyzyjnie mierzyć odstępy czasu. Wystąpił natomiast duży błąd pomiarów wynikający z nieprecyzyjnego rzucania drabinką przez fotokomórkę.

Doświadczenie B bardzo wyraźnie pozwala określić siłę tarcia w zależności od różnych czynników (kąt nachylenia równi, siła nacisku na równię, masa wózka). Rośnie wraz ze wzrostem masy wózka. Widać to wyraźnie przy serii . Maleje natomiast wraz ze wzrostem kąta nachylenia równi pochyłej. Widać to na przykładzie serii. Siła tarcia maleje, mimo iż wzrasta masa wózka i przeciwwagi. Dzieje się tak ponieważ wzrasta kąt a przez to maleje siła nacisku wózka na równię. Uważam, że zastosowanie komputera do tego doświadczenia jest w pełni uzasadnione, gdyż był potrzebny bardzo precyzyjny przyrząd by uchwycić tak małe różnice. Siła tarcia była rzędu 0.1 - 0.2 niutona, a siła ciężkości działająca na wózek i przeciwwagę rzędu 50 niutonów.

Strona: 1

---