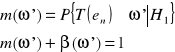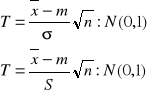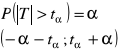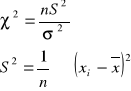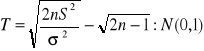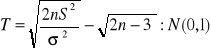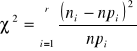HIPOTEZY STATYSTYCZNE: HIPOTEZA STATYSTYCZNA - każdy osąd dotyczący populacji generalnej, wypowiedziany bez przeprowadzenia badania populacji (np. zdanie dotyczące typu rozkładu) HIPOTEZY PARAMETRYCZNE: hipotezy parametryczne (osąd dotyczący parametru) hipotezy proste - specyfikuje czy to parametr lub typ rozkładu hipotezy złożone hipotezy nieparametryczne (zmienna losowa x ma rozkład normalny czy wykładniczy) hipotezy proste - zm. los. x ma rozkład norm. o param. (3,1) hipotezy złożone - zmienna losowa x ma rozkład normalny H - zbiór hipotez dopuszczalnych H0 - hipoteza zerowa H0<H (sprawdzana) (H0 jest to najczęściej element zbioru hipotez dopuszcz.) H1 - hipoteza alternatywna H1 = H - H0 TEST STATYSTYCZNY - jest to jednoznacznie określona reguła postępowania, która w próbie losowej przyporządkowuje decyzje: przyjmij H0, odrzuć H0 Błędy: błąd I rodzaju - odrzucenie sprawdzanej hipotwzy, gdy jest ona prawdziwa błąd II rodzaju - przyjęcie sprawdzanej hipotezy, gdy jest ona fałszywa W - przestrzeń prób T: W→ω eω∈W T - test Funkcja określona na przestrzeni prób, a wartość jest ω ` ω-ω' T(en)∈ω' ⇒H0 odrzucamy, ω' - obszar krytyczny T(en)∈ω-ω' ⇒H0 przyjmujemy, ω-ω' - obszar przyjęć - błąd I rodzaju Prawdopodobieństwo tego, że sprawdzian należy do ω' czyli hipotezę H0 należy odrzucić; odrzucamy tą hipotezę, która jest prawdziwa. - błąd II rodzaju UWAGA: α, β zalezy od ω' Mocą testu - m(ω') - jest to prawdopodobieństwo tego, że odrzucimy hipotezę sprawdzaną pod warunkiem, że zachodzi hipoteza H1. test zgodny TEST ISTOTNOŚCI - uwzględnia jedynie popełnienie błędu I rodzaju α - poziom istotności α = 0,1; 0,05; 0,01; 0,001 Decyzje w sprawie testu istotności: odrzucenie sprawdzanej hipotezy H0 albo brak podstaw do odrzucenia hipotezy H0 UWAGA: Im wyższy poziom istotności x tym większa szansa na odrzucenie H0 ETAPY BUDOWY TESTU ISTOTNOŚCI: określenie hipotezy H0 przyjęcie poziomu istotności α wylosowanie n-elementowej próby prostej i wyznaczenie statystyki zn, której rozkład jest prawdziwy (jest znany) przy założeniu prawdziwości H0 wyznaczenie obszaru krytycznego ω'z wyznaczenie wartości statystyki zn zn∈ω'z ⇒H0 odrzucamy zn∈ωz - ω'z ⇒brak podstaw do odrzucenie H0 TEST ISTOTNOŚCI DLA WARTOŚCI ŚREDNIEJ: H0: m = m0 σ - znane (odchylenie standardowe) ⇒sprawdz. hipotezy H0 ∨ σ - nieznane ; n ≥ 30 σ - nieznane ∧ n ≥ 3 ⇒ sprawdzian gipotezy H0 Rozkład studenta z (n-1) stopniach swobody: obszar krytyczny ω'z H1: m ≠ m0 obszar krytyczny dwustronny obszar krytyczny f(x) -tα tα t H1: m < m0 obszar krytyczny lewostronny f(x) α t -tα H1: m > m0 obszar krytyczny prawostronny f(x) α tα t te - wartość empiryczna statystyki tα - wartość krytyczna odczytana z tablic TEST ISTOTNOŚCI DLA WARIANCJI: x: N(m,σ) σ - nieznane , m - znane lub nieznane H0: σ^2 = σ0^2 H1: σ^2 > σ0^2 n ≤ 30 spr. hip. χ^2 = : rozkład χ o n stopniach swobody a). m - znane m - nieznane spr. hipotezy : rozkład χ^2 o (n-1) stopniach swobody b). m - znane χ^2 = (n-1)S rozkład o (n-1) stopniach swobody X χα^2 χ^2 H1σ1 > σ0^2 P(χ^2 > χα^2) = α χe^2 > χα^2 ⇒ H0 odrzucamy χe^2 - wartość empiryczna statystyki χ^2 UWAGA: spr. hipotezy rozkład χ^2 o (n-1) stopniach swobody n > 30 a). b). TEST ZGODNOŚCI: Warunki stosowalności: dane pochodzą z dużej próby (n duże) dane przedstawione w postaci szeregu rozdzielczego o N(0,r) klas n1 + n2 + ... + nr = n ∧ ni ≥ s ∧ i = 1, 2, ...., r rozkład hipotetyczny ciągły w. skokowy sprawdzian hipotezy H0: rozkład χ^2 o (r-s-1) stopniach swobody s - liczba szacowanych parametrów nipi - liczebność teoretyczna UWAGA: Jeżeli x typu ciągłego to liczebności teoretyczne wyznaczamy z zależności: ϕ - funkcja gęstości xi - środek i-tego przedziału obszar krytyczny wyznaczony z równania: P(χ^2> χα^2) = α χe^2 > χα^2 ⇒ H0 odrzucamy χe^2 - wartość empiryczna statystyki χ^2

ω''''''''''

---