Stat. opisowa - zajmuje się metodami zbierania danych i ich sumarycznego opisu i prezętacji.
Populacja - zbiór jednostek stat powiązanych ze sobą (może być skończona i nieskończona)
Szereg rozdzielczy to dane ułożone według malejącej lub wzrastającej wartości cechy.
Budowa szeregu rozdzielczego obejmuje trzy etapy postępowania:
Ustalenie klas
Zliczanie każdej jednostki statystycznej do odpowiedniej klasy
Zliczanie jednostek w każdej klasie
W pierwszym etapie budowy szeregu rozdzielczego należy określić liczbę klas oraz zakres wartości zmiennej, który każda z klas ma objąć. Kierować się tu możemy następującymi wskazówkami:
Liczba klas nie powinna być mniejsza od 6 i większa od 15.
Klasy powinny być tak ustalone, aby objęły wszystkie wartości zmiennej.
W miarę możliwości należy tworzyć klasy o jednakowej rozpiętości.
środkami przedziałów klasowych powinny być liczby, którymi łatwo operować
Miary położenia:
Średnią arytmetyczną nazywamy sumę jednostek danego zbioru podzieloną przez liczbę tych jednostek. Dla zbiorowości statystycznej składającej się z jednostek o wartościach
x1, x2, ..., xn, średnia arytmetyczna () jest równa:![]()
Dla szeregu rozdzielczego, w którym ni jest liczebnością klasy, a jej środkiem jest xi, średnią arytmetyczną () określa się wzorem: ![]()
![]()
Mediana jest to wartość jednostki, która dzieli uporządkowaną zbiorowość statystyczną na dwie części równe pod względem liczebności. Będzie to więc wartość jednostki znajdującej się w miejscu zbiorowości równym ![]()
Wartość modalna (dominanta) - wartość jednostki w uporządkowanej zbiorowości, której odpowiada największa liczebność. Wartość modalną można określić korzystając z wzoru Pearsona: ![]()
Zgodnie z tym wzorem, po oznaczeniu przez ![]()
stwierdzamy, że wartość modalna leży w odległości 3c od średniej arytmetycznej
Średnia kwadratowa: 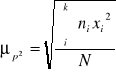
Miary zmienności:
Rozstęp - różnica między największą i najmniejszą wartością cechy.
Wariancją nazywamy średnią arytmetyczną kwadratów odchyleń poszczególnych wartości cechy od jej średniej arytmetycznej.
Wariancję można określić wzorem: 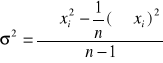
lub 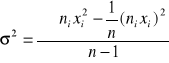
Odchylenie standardowe jest pierwiastkiem kwadratowym wariancji σ ![]()
Odchylenie przeciętne określa się wzorem δ 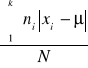
Współczynnik zmienności - jest to odchylenie standardowe wyrażone w procentach średniej arytmetycznej: V = ![]()
Współczynnikiem skośności określamy stopień asymetrii rozkładu. Jeżeli współczynnik skośności ma znak „plus” to wskazuje to na asymetrię dodatnią, a jeżeli ma znak „minus” to na asymetrię ujemną. Im większa jest bezwzględna wartość współczynnika skośności, tym większa jest asymetria rozkładu. ![]()
Zmienna losowa - funkcja która z określonym prawdopodobieństwem przyporządkowuje zdarzeniom elementarnym liczby rzeczywiste
Zmienna losowa X funkcja X przyporządkowująca każdemu zdarzeniu elementarnemu 1 i tylko 1 liczbę.
Skokowa - gdy może przyjmować skończoną lub nie skończoną ale przeliczalną liczbę wartości
Ciągła - gdy jej możliwe wartości tworzą przedział ze zbioru liczb rzeczywistych.
Dystrybuanta zmiennej losowej X to prawdopodobieństwo przyjęcia przez zmienną losową X wartości >= X
Zmienna losowa X ma rozkład dwumianowy, jeżeli jej funkcja prawdopodobieństwa określona jest wzorem
P(X = k) =![]()
, gdzie q = 1-p, i k = 0, 1, 2, ..., n. ![]()
, ![]()
Zmienna losowa X ma rozkład normalny, jeżeli jej funkcja gęstości określona jest wzorem: 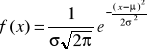
Wyszukiwarka
Podobne podstrony:
stata II, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Statystyka, ściągi
ściąga wg mnie, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, ściągi
sciagazarz, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, Cwiczenia, ściągi
sciaga egzamin, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, ściągi
spółki, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, ściągi
Ekonomika ćw II, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Ekonomika, Ściągi
ZARZ$D~2, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, ściągi
tematy sprawozdań, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Statystyka
ZARZĄDZANIE EGZ 2, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, ściągi
ZARZADZANIE EGZ 1a, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, ściągi
ZARZ$D~3, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, ściągi
ZARZ$D~1, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, ściągi
ZARZĄDZANIE EGZ 3a, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, ściągi
Ekonomika ćw I, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Ekonomika, Ściągi
Ekonomika ćw II duze, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Ekonomika, Ściągi
ZARZĄDZANIE EGZ 3, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, ściągi
spółki, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, ściągi
Aktywa-kolokwium, Niezbędnik leśnika, WYDZIAŁ LEŚNY, Zarządzanie, Cwiczenia, ściągi
więcej podobnych podstron