POLITECHNIKA CZĘSTOCHOWSKA
WYDZIAŁ BUDOWNICTWA
SAMODZIELNY ZAKŁAD WYTRZYMAŁOŚCI MATERIAŁÓW
Ćwiczenia laboratoryjne nr 8
TEMAT: Badanie wyboczenia pręta ściskanego.
DANE STUDENTA:
Magdalena Duszyńska
Budownictwo
Grupa 2
Studia Dzienne
Rok Akad. 2010/2011
1.CZĘŚĆ TEORETYCZNA.
Wyboczenie - w wytrzymałości materiałów odkształcenie (wygięcie) osiowo ściskanego pręta. Teoretycznie, gdy pręt jest idealnie symetryczny, a siła ściskająca idealnie osiowa i centryczna, wyboczenie nie ma prawa wystąpić. W rzeczywistych układach taki warunek jest jednak bardzo rzadko spełniony. Pręty zawsze mają pewne niedokładności wykonania, siły mogą być przykoszone lub obciążać pręty ekscentrycznie. W takiej sytuacji przy odpowiednio dużym obciążeniu, większym niż obciążenie dopuszczalne Pdop, istnieje niebezpieczeństwo wyboczenia. Wyboczenie może być sprężyste, to znaczy takie, gdy po odciążeniu pręta wraca on do pierwotnego, wyprostowanego kształtu, lub niesprężyste, gdy pręt utrzymuje swój wyboczony kształt także po odciążeniu. [1]
Wyboczenie pręta ściskanego osiowo jest jednym z przykładów utraty stateczności. W przypadku wyboczenia zniszczenie pręta następuje nie poprzez przekroczenie wytrzymałości na ściskanie lecz poprzez zmianę jego kształtu i związanej z tym zmiany charakteru stanu naprężenia w pręcie. [2]
W przypadku ściskania prętów stosunkowo krótkich (pręty krępe) wymiary przekroju poprzecznego wyznacza się z warunku wytrzymałościowego:
![]()
(1)
Natomiast wymiarowanie prętów smukłych przebiega z uwzględnieniem smukłości. Zniszczenie pręta smukłego może nastąpić nie ze względu na przekroczenie jego wytrzymałość na ściskanie, lecz na skutek zmiany jego kształtu i związanej z tym zmiany charakteru stanu naprężenia - oprócz ściskania pojawi się zginanie, czyli naprężenia określać będzie wzór:
![]()
(2)
[3]
Kształt osi pręta przy danej sile ściskającej - prostoliniowy lub krzywoliniowy - zależy od rodzaju odpowiedniego stanu równowagi. Ich interpretacją graficzną jest kula spoczywająca na powierzchni.
Rys.1. Modele równowagi układów mechanicznych, a) równowaga trwała, b) równowaga chwiejna,
c) równowaga obojętna [2]
Pierwszym stanem równowagi jest równowaga trwała. Charakteryzuje się on tym, że po niewielkim wytrąceniu z położenia równowagi układ stara się wrócić do tego położenia, gdy ustanie przyczyna zakłócenia.
Drugim stanem równowagi jest równowaga chwiejna. Charakteryzuje się on tym, że nawet bardzo małe zakłócenie jest w stanie wytrącić go z położenia równowagi. Układ taki będzie w dalszym ciągu dążył do innego położenia równowagi, jeżeli taki istnieje.
Trzecim stanem równowagi jest równowaga obojętna. Jest to stan pośredni pomiędzy stanem równowagi trwałej i chwiejnej. Charakteryzuje się on tym, że małe zakłócenie nie powoduje zmiany jego stanu równowagi. Układ przesunięty z jednego położenia w sąsiednie pozostaje w tym nowym położeniu równowagi. [2]
Przeanalizujmy teraz swobodnie podparty pręt obciążony siłą skupioną P równoległą do jego osi. Jeśli siła ściskająca P jest mała, możliwa jest tylko postać równowagi trwałej. Pręt wychylony z konfiguracji początkowej po odciążeniu do niej wraca. Jego równowaga będzie trwała (stateczna) jeśli po jego wygięciu wskutek przyłożenia dowolnie małego czynnika zakrzywiającego (np. siły ΔS prostopadłej do osi pręta) i po usunięciu tego czynnika pręt wyprostuje się (powróci do sytuacji pierwotnej) - rys. 2
Rys. 2 - Pręt obciążony siłą P < Pkr Rys. 3 - Pręt obciążony siłą P > Pkr
Równowaga pręta będzie chwiejna (niestateczna), jeżeli po usunięciu chwilowego czynnika zakrzywiającego pręt pozostanie nadal wygięty, a więc nie powróci do swej pierwotnej postaci, natomiast nowa, zakrzywiona postać równowagi będzie natomiast trwała (stateczna) - rys.3.Równowaga obojętna jest stanem rozgraniczającym równowagę stateczną i niestateczną. [3],[7]
Najmniejsza wartość siły P potrzebna do wyprowadzenia pręta ze stanu równowagi statecznej
do niestatecznej nosi miano siły krytycznej Pkr.
Stan równowagi pręta ściskanego zależy od:
- siły ściskającej P
- długości pręta l
- sztywności giętej EJ
- warunków brzegowych (zamocowania) [6]
W warunkach rzeczywistych, wykonanie idealnie prostego pręta i idealne przyłożenie
obciążenia P nie jest możliwe.
Rys. 4. Zależność przemieszczenia osi pręta i osiowej siły ściskającej [2]
Siłę krytyczna ustala się na bazie równania krzywizny wygiętego pręta 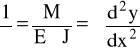
(3)
Wygięcie pręta jest wywołane momentem zginającym M = P · y.
Po podstawieniu otrzymujemy
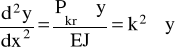
(4)
gdzie : 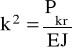
(5)
Całka ogólna powyższego równania różniczkowego jest funkcja trygonometryczna:
![]()
(6)
Stałe całkowania C1 i C2 ustala się na podstawie warunków brzegowych:
1) x = 0, y = 0
2) x = L, y = 0
i otrzymuje: C2 = 0 i C1 · sin(k · l) = 0. Równania jest prawdziwe, gdy sin(k · l) = 0, tzn gdy
k · l przybiera wartości równe: 0, π, 2 π, 3 π , ..., n π . Jednocześnie, ani k, ani l nie mogą być
równe 0, zatem pierwsze rozwiązanie otrzymujemy, gdy iloczyn k · l = π.
Ostatecznie, gdy k · l = π siła krytyczna jest równa:
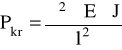
(7)
gdy k · l = 2π siła krytyczna jest równa :
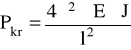
(8)
oraz gdy k · l = 3π siła krytyczna jest równa:
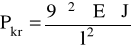
(9)
Powyższe wzory nosa nazwę wzorów Eulera. [2]
Pręt poddany wyboczeniu ma tendencje do wychylania się w płaszczyźnie najmniejszej sztywności, której odpowiada najmniejszy moment bezwładności.
Naprężenia spowodowane siła krytyczna określa się naprężeniami krytycznymi:
![]()
(10)
gdzie : ![]()
(11)
jest smukłością pręta odpowiednio w kierunku x lub y, a
![]()
(12)
długością wyboczeniowa pręta. [4]
2. PRZEBIEG ĆWICZENIA.
Badanie przeprowadzone może być na specjalnie zbudowanym do tego celu stanowisku lub na maszynie wytrzymałościowej.
A) Badanie wyboczenia pręta na stanowisku pomiarowym :
Badany pręt 1 o końcach podpartych przegubowo umieszczony jest w statywie 2. Siła ściskająca pręt realizowana jest za pomocą dźwigni jednostronnej 3 opierającej się na nim poprzez kulkę 4 i suwak 5. Wartość siły ściskającej ustala się przesuwając wzdłuż ramienia dźwigni obciążnik 6 i zawieszając na szalce obciążniki 7. Przeciwwaga 8 służy do wyeliminowania wpływu na obciążenie pręta ciężaru dźwigni i pustej szalki. Do statywu 2 przymocowany jest czujnik zegarowy 9 mierzący ugięcie f pręta 1 w połowie jego długości.
Przebieg ćwiczenia :
1) Obliczyć silę krytyczna dla badanego pręta.
2) Wyzerować czujnik zegarowy 9.
3) Zwolnic dźwignie 3 wysuwając znajdujący się pod nią klocek zabezpieczający.
4) Za pomocą przesuwnego obciążnika 6 obciążyć pręt siła P0=900N, odczytać wskazanie f czujnika. Wartość siły P0 oraz ugięcie pręta zanotować w tabeli protokołu.
5) Dalsze zwiększanie siły ściskającej pręt realizować poprzez układanie obciążników na szalce. W tabeli protokołu notować wskazanie f czujnika 9, obciążenie P0 oraz obciążenie PS szalki. Liczbę przypadków obciążenia ustalić z prowadzącym ćwiczenie. Maksymalna siła obciążająca pręt nie może przekroczyć 90% obliczonej wcześniej siły krytycznej.
6) Odciążyć całkowicie pręt. Stanowisko przywrócić do stanu początkowego. [5]
Rys.5. Stanowisko do badania wyboczenia pręta ściskanego [5]
B) Badanie wyboczenia pręta na maszynie wytrzymałościowej
Ściskanie siła P stalowego pręta 1 przeprowadzane jest na maszynie wytrzymałościowej. Końce pręta umieszczone są w gniazdach 2 zapewniających jego przegubowe podparcie. Czujnik zegarowy 3 służy do pomiaru strzałki ugięcia f pręta w środku jego długości.
Przebieg ćwiczenia :
1) Obliczyć silę krytyczna dla badanego pręta.
2) Włączyć maszynę wytrzymałościową i uruchomić program sterujący.
3) Ustawić pręt w gniazdach.
4) Przy nie obciążonym pręcie wyzerować siłomierz maszyny.
5) Ustawić prędkość przesuwu trawersy maszyny na 0.1mm/min.
6) Obciążyć pręt siła wstępną około 50N.
7) Wyzerować położenie trawersy maszyny.
8) Ustawiać dolny ogranicznik ruchu trawersy na dolnej krawędzi czujnika.
9) Ustawić czujnik zegarowy w środku pręta, prostopadle do jego płaszczyzny i wyzerować.
10) Obciążać pręt kolejno siłami: 1000N, 1380N, 1560N, 1680N, 1750N,
1810N, 1850N, 1880N, 1900N, 1925N, 1950N i każdorazowo odczytywać wskazania czujnika zegarowego. Wyniki (siła P, strzałka ugięcia f) notować w tabeli protokołu.
11) Odciążyć pręt przez powrót trawersy do pozycji początkowej
12) Przesunąć trawerse w góre i wyjca pręt. [5]
Rys.6. Schemat stanowiska do badania wyboczenia perta ściskanego
na maszynie wytrzymałościowej [5]
3. Bibliografia
Banasiak M., Ćwiczenia laboratoryjne z wytrzymałości materiałów PWN 2000r
Niezgodziński M., Niezgodziński T., Wytrzymałość materiałów
www.wikipedia.pl
www.ikb.poznan.pl
www.tu.kielce.pl/publikacje/dydaktyczne/wbiis/kwm
www.forumbudownictwa.pb.bialystok.pl
www.dziewiecki.pr.radom.pl
Wyszukiwarka
Podobne podstrony:
6.Wyznaczanie modułu sprężystości postaciowej G przez pomiar kąta skręcenia pręta, Budownictwo pcz,
4.Modelowe badania elastooptyczne, Budownictwo pcz, referaty wytrzymka lab
3.Tensometria oporowa, Budownictwo pcz, referaty wytrzymka lab
statyczna pr rozcia, Budownictwo pcz, referaty wytrzymka lab
wyboczenie pręta ściskanego, budowictwo pcz (h.fresh06), II rok (sem III i sem IV), sem IV, wytrzyma
Badanie wyboczenia pręta ściskanego, PSW budownictwo projekty i inne
sciaga badanie konsystencji, Budownictwo PCz, Technologia betonów i zapraw, Ściągi
sciaga Sposoby-badania-modulu-odksztalcenia-2, Budownictwo PCz, Bud. Komunikacyjne
ZGINANIE ZE ŚCISKANIEM, Budownictwo PK, Wytrzymałość materiałów, semestr 2
sciskanie, Budownictwo AGH 1, Wytrzymka
Wyznaczanie rozkładu naprężeń normalnych i stycznych w przekroju belki zginanej, Budownictwo PCz, Wy
logoń,materiały budowlane L, badanie wytrzymałości betonu na ściskanie przy pomocy prasy wytrzymałoś
Bud. na terenach górniczych, Budownictwo pcz, różne
BADANIE PR BEK, Resources, Budownictwo, Mosty, LABORKI BAD KONSTRMOSTOWYCH, INNE
warunki gruntowe, Budownictwo PCz, Bud. Komunikacyjne
matateoria, BUDOWNICTWO PCZ I rok, Matematyka
więcej podobnych podstron