Funkcje wielomianowe

Funkcjami wielomianowymi nazywamy wszystkie te funkcje, których wzór ma postać y = W(x), gdzie W(x) jest wielomianem. Dziedziną funkcji wielomianowej jest zbiór liczb rzeczywistych.

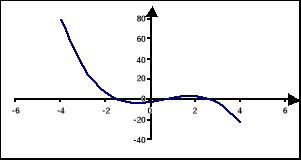
y = -x³ + 2x² + 3x -3

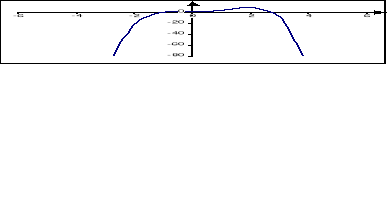
y = -x⁴ + 2x³ + 2x² + 1

Funkcje: liniowa i kwadratowa, to przykłady funkcji wielomianowych odpowiednio stopnia pierwszego i drugiego których własności znamy.

Jak wiemy z własności funkcji kwadratowej, wykresy funkcji postaci y = ax² przechodzą przez początek układu współrzędnych. Tak również dzieje się wówczas, gdy n jest liczbą naturalna większą od 2.

Jeśli n jest liczba parzystą, to wykres funkcji y = axⁿ ma oś symetrii, która jest oś y. W zależności od wartości współczynnika a funkcja może przyjmować tylko wartości nieujemne (dla a>0)

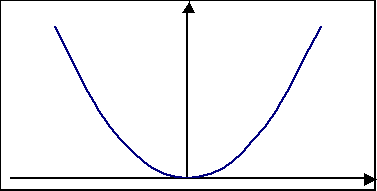
lub tylko niedodatnie (dla a<0)

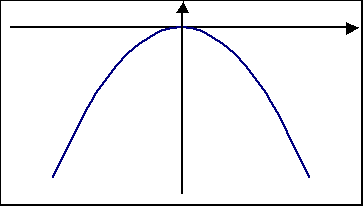
Jeśli n jest liczba nieparzystą, to wykres funkcji y = axⁿ ma środek symetrii, którym jest początek układu współrzędnych. Gdy współczynnik a jest liczba dodatnią funkcja może być rosnąca.

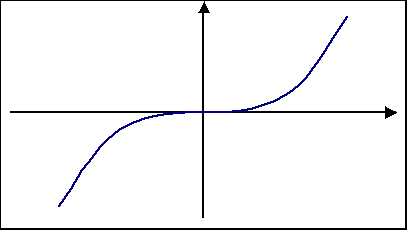
Gdy współczynnik a jest liczba ujemną funkcja może być malejąca.

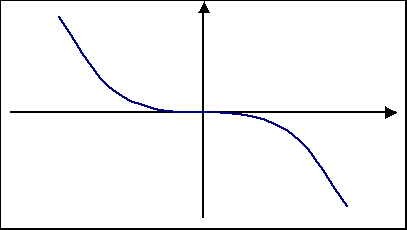
Jeśli W(x) jest wielomianem stopnia nieparzystego , to funkcja wielomianowa y = W(x) ma co najmniej jedno miejsce zerowe.

Jeśli funkcja wielomianowa postaci

y = a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 + ... + a₃x³ + a₂x² + a₁x + a₀

gdzie a_n > 0 , ma miejsca zerowe, to dla argumentów większych od wszystkich miejsc zerowych wartości funkcji są dodatnie. Jeśli taka funkcja nie ma miejsc zerowych, to wszystkie wartości są dodatnie.

Jeśli funkcja wielomianowa postaci

y = a_nxⁿ + a_n-1x^n-1 + a_n-2x^n-2 + ... + a₃x³ + a₂x² + a₁x + a₀

gdzie a_n < 0 , ma miejsca zerowe, to dla argumentów większych od wszystkich miejsc zerowych wartości funkcji są ujemne. Jeśli taka funkcja nie ma miejsc zerowych, to wszystkie wartości są ujemne.

Jeśli a jest pierwiastkiem wielomianu W(x), to wykres funkcji postaci y = W(x) przechodzi prze punkt (a,0). Przy przejściu przez ten punkt wykres pozostaje po tej samej stronie osi x (znak funkcji się nie zmienia), gdy a jest parzystokrotnym pierwiastkiem.

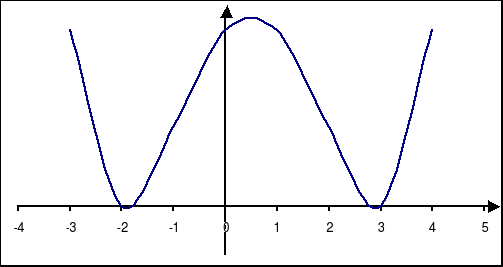
Liczby: -2 i 3 są dwukrotnymi pierwiastkami wielomianu W(x) = (x + 2)²(x - 3)²

Jeśli a jest pierwiastkiem nieparzystokrotnym, to wykres funkcji y = W(x) przy przejściu przez punkt (a,0) przechodzi na drugą stronę osi x - zmienia się znak wartości funkcji.

Ćwiczenie 1

Rozwiąż zadania:1, 4 str.50, 5, 7 str. 51, 8, 11 str. 52 z podręcznika.

---