Dany jest wzór funkcji y=x2+bx. Wyznacz parametr b tak, aby:
do wykresu funkcji należał punkt A=(-1,3).
miejscem zerowym funkcji była liczba 4.
funkcja miała tylko jedno miejsce zerowe.
Dany jest wzór funkcji y=x2+b. Ustal parametr b tak, aby:
do wykresu funkcji należał punkt A=(2,3).
funkcja miała miejsca zerowe -1 i 1.
do wykresu funkcji należał punkt B=(-1, 1).
Dana jest funkcja y=x2+3x+c. Wyznacz parametr c tak, aby:
do wykresu funkcji należał punkt A=(-1,3).
funkcja miała miejsce zerowe 1.
wykres był styczny do osi x.
Wyznacz współczynniki b i c trójmianu y=x2+bx+c tak, aby do wykresu trójmianu należały punkty A i B.
a) A=(1,1) B=(0,-5) b) A=(3,9) B=(-1,9)
c) A=(![]()
,6) B=(3![]()
,18) d) A=(![]()
,1) B=(2,-3)
Wyznacz największą wartość funkcji w podanym przedziale:
y=-2x2+x-1 x

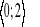
y=-x2-3x+10 x

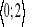
y=2x2-x+1 x

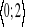
y=x-x2 x

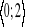
Wyznacz najmniejszą wartość funkcji w podanym przedziale:
y=x2+4x-2 x

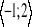
y=2x2-1,5x+0,6 x

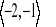
y=x2-1 x

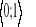
Dane są funkcje kwadratowe. Wyznacz miejsca zerowe, współrzędne wierzchołka paraboli i punkt przecięcia wykresu z osią x dla każdej funkcji.
y=x2-7
y=x2+
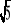
x2-6x
y=x2+8x+16
Naszkicuj wykres funkcji f(x)=x2-8x+15, a następnie rozwiąż graficznie nierówności f(x)>0, f(x)

0, f(x)
0.Rozwiąż nierówności:
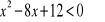
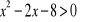
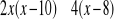
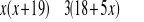
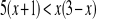
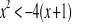
Dane są funkcje y=f(x) i y=q(x). Na jednym rysunku sporządź wykresy obu funkcji i odczytaj rozwiązanie nierówności
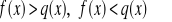
i równania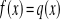
, a następnie rozwiąż nierówności sposobem rachunkowym.f(x)=x2+2x-8 q(x)=2x-8
f(x)=-x2+6x-5 q(x)=3x-3
f(x)=8x+8 q(x)=2x2+8x+6
f(x)=-4x+8 q(x)=-3x2+5x+2
Wyszukiwarka
Podobne podstrony:
miejsca zerowe funkcji kwadratowej, Matematyka, Liceum
funkcja kwadratowa, Matematyka, Liceum
funkcja kwadratowa 2, Matematyka, Liceum
Funkcja kwadratowa, Matematyka - zadania liceum
Funkcja kwadratowa, Sprawdziany, Liceum, Matematyka
kwadratowa, Matematyka, Liceum
Funkcja kwadratowa, matematyka
FUNKCJA KWADRATOWA, Matematyka
równania i nierówności kwadratowe, Matematyka, Liceum
funkcja wykładnicza, Matematyka, Liceum
kwadratowa (2), Matematyka, Liceum
kwadrat, Matematyka, Liceum
Zastosowania funkcji kwadratowej, Matematyka. Zadania i rozwiązania
równania kwadratowe, Matematyka, Liceum
przeksztalcenie funkcji homograficznej, Matematyka, Liceum
funkcja własności, Matematyka, Liceum
nierówności kwadratowe, Matematyka, Liceum
funkcja własności2, Matematyka, Liceum
więcej podobnych podstron