Statystyka

Literatura podstawowa

1.Augustyniak H. Statystyka opisowa z elementami demografii, Poznań 2003.

2.Makać W. Podstawy statystyki i demografii. UG, Gdańsk 2003.

3.Kassyk- Rokocka H. Statystyka - zbiór zadań, Warszawa 2001

Literatura uzupełniająca

1. Holzer J.Z. Demografia, PWE warszawa 2004.

2. S. Ostasiewicz, Z. Rusnak, u. Siedlecka - Statystyka. Elementy teorii
   i zadania. WAE, Wrocław 2001

3. strona internetowa http://www.stat.gov.pl

4. Roczniki statystyczne GUS

1. Próba statystyczna, metody prezentacji danych

1. Populacja i próba statystyczna

Statystyka jest to nauka zajmująca się opisywaniem i analizą prawidłowości zjawisk masowych.

Przez badanie statystyczne rozumie się ogół prac mających na celu poznanie struktury określonej zbiorowości statystycznej.

Celem badań statystycznych jest poznanie prawidłowości ilościowych i jakościowych w masowych zjawiskach losowych i opisywanie ich za pomocą liczb.

Niech Z oznacza zbiór elementów podlegających badaniu ze względu na jedną lub więcej własności, nazywanych cechami.

Jeśli Z jest zbiorem elementów mających przynajmniej jedną własność wspólną i przynajmniej jedną, którą te elementy się różnią, nazywamy populacją lub zbiorowością statystyczną.

Elementami zbioru Z mogą być ludzie, zwierzęta, rośliny, przedmioty itp.

Bezpośredniej obserwacji lub pomiarowi podlegają własności elementów populacji nazywanych jednostkami statystycznymi

Badać można wszystkie elementy danej populacji statystycznej, zwanej też populacja (zbiorowością) generalna, albo tylko ich część, nazywaną próbką statystyczną (próbką).

• — W pierwszym przypadku badanie jest kompletne i dostarcza pełnych informacji o badanej własności.

• — W drugim przypadku badanie jest częściowe.
  Zadaniem statystyki jest wnioskowanie o własnościach całej populacji Z na podstawie informacji o tych własnościach elementów pewnego skończonego podzbioru Z1 tej populacji, zwanego próbką.

Próbka Z1 stanowi reprezentację populacji Z.

Próbka losowa n-elementowa prosta to próbka n-elementowa wylosowana
z populacji, przy czym każdy n-elementowy podzbiór populacji generalnej ma takie same szanse wylosowania.

n nazywamy liczebnością próbki losowej.

Odmiany lub wartości badanej cechy otrzymane z pomiarów lub obserwacji

tej cechy u jednostek próbki oznaczamy x₁, x₂, … , x_n.

1. Cechy statystyczne

Elementy populacji generalnej mogą mieć różne właściwości, które podlegają obserwacji statystycznej.

Nazywamy je cechami statystycznymi i oznaczamy dużymi literami np.: X, Y, Z, a ich wartości odpowiednio małymi :x_i , y_i , z_{i, …}

Cechy statystyczne dzielimy je na:

• jakościowe (niemierzalne) - Odmian(warianty) cechy jakościowej nie da się określić za pomocą liczb, np. płeć, rasa, kolor skóry, poziom wykształcenia.

• ilościowe ( mierzalne) - Odmiany cechy mierzalnej wyraża się liczbami, np. wysokość, ciężar, wytrzymałość, liczba połączeń telefonicznych w ciągu jednostki czasu itp.

Cechy mierzalne dzielimy na:

• ciągłe - wartość cechy może być dowolną liczbą z pewnego przedziału liczbowego,

• skokowe (dyskretne ) - wartości należą do pewnego skończonego podzbioru liczb, najczęściej całkowitych.

Statystyka opisowa zajmuje się wstępnym opracowaniem próbki bez posługiwania się rachunkiem prawdopodobieństwa

1. Metody prezentacji danych

Dane otrzymane z pomiarów lub obserwacji należy odpowiednio uporządkować i ewentualnie pogrupować w postaci tzw. szeregów statystycznych.

Niech x₁, x₂, … , x_n , n ≥ 1, będzie n elementową próbką pobraną z populacji.

Jeśli liczebność n próbki jest większa od 30, próbę nazywamy dużą,
jeśli n ≤ 30, próbę nazywamy małą.

Szeregiem szczegółowym nazywamy uporządkowany ciąg wartości badanej cechy.

W takiej postaci pozostawiamy dane, gdy próbka jest mała, tzn. badaniu zastała poddana niewielka ilość jednostek populacji.

Jeśli cecha X przyjmuje wartości x₁, x₂,…x_n ., w szeregu szczegółowym spełniają one warunek

x₁ * x₂ *… * x_n .

Jeśli n≥ 30, próbkę nazywamy dużą wartości x₁, x₂, … , x_n grupuje się w klasy tj. przedziały liczbowe o najczęściej jednakowej długości w przypadku cech ciągłych, lub klasami są różne wartości cechy, dla cech skokowych.

W pierwszym przypadku mówimy o szeregach rozdzielczych z przedziałami klasowymi, w drugim o szeregach punktowych.

Rozstępem badanej cechy w próbce nazywamy różnicę

R=x_max - x_min

Istnieje kilka reguł ustalania orientacyjnie liczby k klas szeregów rozdzielczych

przedziałowych w zależności od liczebności próbki n.

k ≤ 5ln (n), k=1+3,322ln (n), k * *n

Można również korzystać z orientacyjnych danych umieszczonych w tabelce.

Liczba obserwacji n	Liczba klas k
40 - 60 60 - 00 100- 200 200 - 500 500 -1500	6- 8 7 - 10 9 - 12 11 - 17 16 - 25

Za długość klasy przyjmuje się

h* R / k .

Szereg rozdzielczy z przedziałami klasowymi ma postać:

Wartości cechy	Liczebności empiryczne
x10 - x11	n1
x20 - x21	n2
x30 - x31	n3
: :	: :
xk0 - xk1	nk

Jeśli występuje duża koncentracja wartości cechy w jednym przedziale, stosujemy wtedy różne rozpiętości.

<x_i0 ; x_i1) - i- ty przedział klasowy. Przyjmujemy, że przedziały klasowe są prawostronnie otwarte.

x_i0- początek i- tego przedziału klasowego,

x_i1 - koniec i- tego przedziału klasowego.

n_i -liczebności poszczególnych przedziałów klasowych, i=1, 2, …,k.

k - liczba przedziałów klasowych, n - liczebność próby.

.

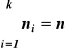
n_i - określają, ile liczb spośród wartości próbki zawartych jest w i-tym przedziale klasowym.

h_i = x_i1- x_i0 nazywamy rozpiętością lub długością i-tego przedziału klasowego.

nazywamy środkiem i-tego przedziału klasowego.

Dla cech mierzalnych skokowych, przy niewielkiej liczbie różnych wartości x₁, x₂, … , x_k, buduje się szeregi punktowe. Mają one postać:

Wartości cechy	Liczebności empiryczne
x1	n1
x2	n2
x3	n3
: :	: :
xk	nk

Wskaźnikiem struktury lub częstością względną ( frakcją , odsetkiem) występowania i - tego wariantu cechy nazywamy

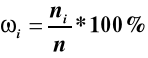
i=1, 2, …k lub

Wartości, ω_i , i=1, 2, …k określają, jaka część lub procent jednostek populacji
przyjmuje wartości cechy w i-tym przedziale klasowym .

Liczebności skumulowane definiujemy:

, i=1, 2, …k.

Odpowiednio, częstości względne skumulowane

, i=1, 2, …k.

Częstości względne skumulowane określają, jaka część ( lub procent) jednostek populacji przyjmuje wartości cechy mniejsze od końca w i-tego przedziału klasowego.

Przykład 1

Z populacji generalnej pobrano próbę n=50 elementową i otrzymano wartości badanej cechy X:

3,6 ; 5,0 ; 4,0 ; 5,2 ; 4,7 ; 5,9 ; 4,5 ; 5,3 ; 5,5 ; 3,9 ; 5,6 ; 3,5 ; 5,4 ; 5,2 ; 4,1 ; 5,0 ; 3,1 ; 5,8 ; 4,8 ; 4,4 ; 4,6 ; 5,1 ; 4,7 ; 3,0 ; 5,5 ; 6,1 ; 3,8 ; 4,9 ; 5.6 ; 6,1 ; 5,9 ; 4,3 ; 6,4 ; 5,3 ; 4,5 ; 4,0 ; 4,0 ; 5,2 ; 3,3 ; 5,4 ; 4,7 ; 6,4 ; 5,1 ; 3,4 ; 5,2 ; 6,2 ; 4,4 ; 4,3 ; 5,8 ; 3,7 .

Utworzyć szereg rozdzielczy. Wyznaczyć wskaźniki struktury, liczebności skumulowane wskaźniki struktury skumulowane.

Liczba klas k**50 * 7

Rozpiętość R=x_max - x_min =6,4 - 3,0 = 3,4

R/k * 0,49 *0,5

Wartości cechy xi	Środki przedziałów	Liczebności ni	Liczebności skumulowane nisk	Częstości względne ωi	Częstości względne ωisk
2,9 - 3,4	3,15	4	4	0,08	0,08
3,4 - 3,9	3,65	5	9	0,10	0,18
3,9 - 4,4	4,15	7	16	0,14	0,32
4,4 - 4,9	4,65	9	25	0,18	0,50
4,9 - 5,4	5,15	12	37	0,24	0,74
5,4 - 5,9	5,65	8	45	0,16	0,90
5,9 - 6,4	6,25	5	50	0,10	1
*		50	X	X

2. Prezentacja graficzna szeregów

Szeregi rozdzielcze przedstawia się graficznie za pomocą tzw. histogramów lub diagramów..

Histogram jest zbiorem prostokątów, których podstawy zaznaczane
są na osi odciętych i są wyznaczone przez granice przedziałów klasowych, wysokości tych prostokątów określają liczebności (lub wskaźniki struktury, liczebności skumulowane lub częstości skumulowane) poszczególnych klas.

Diagram jest linią łamaną łączącą środki górnych boków prostokątów histogramu.

Histogram i diagram szeregu z poprzedniego przykładu

| | | | | | | | | |

Przykład 2

Strukturę gospodarstw według liczby osób w gospodarstwie domowym i miejsca zamieszkania w województwie pomorskim w 2006r. przedstawia tabelka:

Liczba osób w gospodarstwie xi	Liczba gospodarstw		Wskaźniki struktury		Minimum ( ωmi , ωwi )
		miasto nmi	wieś nwi	ωmi		ωwi
1	166130	39555	0,2850	0,1800	0,1800
2	156213	44350	0,2680	0,2019	0,2019
3	126175	44320	0,2165	0,2018	0,2018
4	91312	45165	0,1567	0,2056	0,1567
5 i więcej	43036	46262	0,0739	0,2106	0,0739
Razem	582866	219652	1	1	0,8143

Źródło: Rocznik statystyczny 2006 i obliczenia własne.

Wskaźnik podobieństwa struktur stosuje się do pomiaru podobieństwa rozkładów populacji,

Przy czym
.

Im ω_p bliższy jest watrości 1, tym struktury badanych zbiorowości są bardziej podobne.

W przykładzie 2 ω_p=0,8143 co świadczy o dużym podobieństwie rozkładów populacji „miasto” i „wieś” badanych pod względem ilości osób
w gospodarstwach domowych.

4

Wykład 1 Statystyka i demografia Administracja 1

3

_ωi

n_i

0 2,9 3,4 3,9 4,4 4,9 5,4 6,0 6,4 x

24%

20%

16%

12%

8%

4%

12

10

8

6

4

2

diagram

---