I MDM data: 18,03,2003 gr 62

zespół.

Gwizdak Przemysław

Sprawozdanie z ćwiczenia nr 21.

Temat:Rozładowanie kondensatora.

I Wstęp:

1. Pojemność elektryczna - definicja, rodzaje kondensatorów.

Pojemność kondensatora zdefiniowana jest jako stosunek ładnku zgromadzonego na jednej z okładek do napięcia pomiędzy okładkami.

2. Rozładowanie i ładowanie kondensatora, równanie krzywej ładowania i rozładowania, stała czasowa obwodu.

W chwili początkowej tzn. dla t = 0 napięcie na kondensatorze U_c = 0. Po upływie czasu t ładunek zgromadzony na okładce kondensatora można wyrazić zależnością :

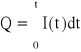
W chwili początkowej t = 0 ładunek na kondensatorze wynosi U₀.

Zgodnie z I prawem Kirchoffa:

U_c = U_R

3. Wyznaczenie pojemności kondensatora na podstawie jego krzywej rozładowania.

4. Wyznaczenie wartości ładunku zgromadzonego na okładkach kondensatora na podstawie krzywej rozładowania.

II Wykonanie ćwiczenia:

1. Połączyć układ wg. schematu. Odczytać wartość oporu z opornicy dekadowej.

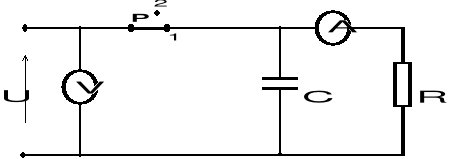
2. Naładować kondensator, gdy wartość prądu ustali się przyjąć ją jako I0 dla chwili t = 0 (s).

3. Przełączyć przełącznik P i jednocześnie włączyć sekundomierz. Przeprowadzić pomiary natężenia prądu rozładowania kondensatora I = f(t).

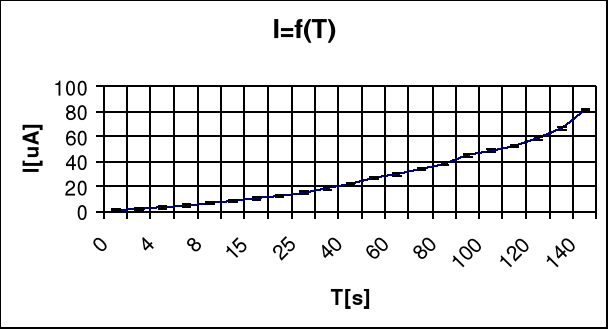
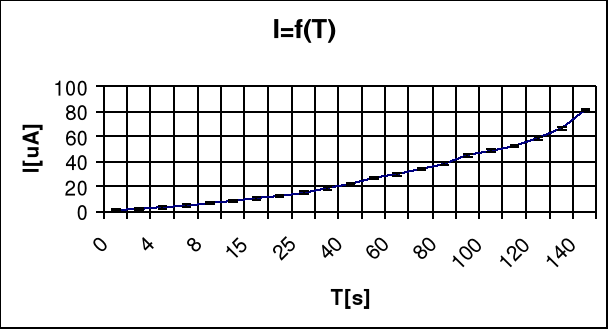
4. Sporządzić wykres prądu rozładowania : I = f(t) oraz wykres
.

5. Wartość ładunku zgromadzonego na okładkach kondensatora można obliczyć wyznaczając wartość pola powierzchni zawartego pomiędzy osiami współrzędnych a wykresem I = f(t).

6. Wyznaczyć pojemność kondensatora :

gdzie : Q - wartość ładunku zgromadzonego na okładkach kondensatora,

U - napięcie między okładkami, które w tym przypadku jest równe napięciu zasilającemu obwód pomiarowy.

7. Obliczyć stałą czasową obwodu korzystając z wykresu

U = 5V; R = 34kΩ; Io = 150μA; C = 470μF
T	I	Q	C
[ s ]	[μA ]	[ μC ]	[ μF ]	[ s ]
1,59 2,42 3,84 5,20 6,52 8,48 10,62 12,64 15,54 18,62 22,24 26,85 30,14 33,94 38,48 44,75 48,68 52,79 58,50 66,56 81,38	140 130 120 110 100 90 80 70 60 50 40 30 25 20 15 10 8 6 4 2 0	2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05 2132,05	426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41 426,41	14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50 14,50

Ładunek zgromadzony na okładkach kondensatora wyznaczamy licząc pole powierzchni pod krzywą I = f(t) ( patrz rys. 1 ) jako sumę pól trapezów wyznaczonych przez punkty pomiarowe. Możemy tak postąpić ponieważ zaproksymowana krzywa zawiera te punkty i błąd jaki popełniamy jest niewielki.

- woltomierz : kl 0.5% ; zkres 7.5V

- mikroamperomierz : kl 0,5% ; zakres 150μA

6. Wyznaczyć pojemność kondensatora :

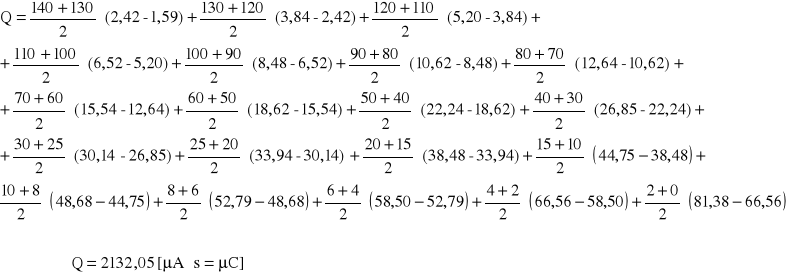
Pojemność badanego kondensatora wynosi :

Stała czasowa obwodu = R C jest równa:

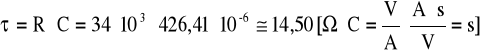
Błędy mierników:

bezwzględny :

względny procentowy :

gdzie k - klasa dokładności miernika

ZP - zakres pomiarowy miernika

XM - wartość mierzona

Błąd pomiaru napięcia:

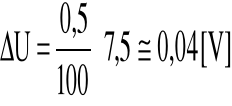
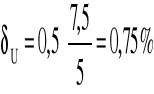
Błąd pomiaru prądu :

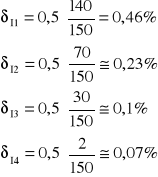
Błąd bezwzględny pomiaru czasu określamy jako czas reakcji wykonującego pomiar

błąd względny :

Szacowanie błędu w obliczeniach ładunku :

Ładunek zgromadzony na okładkach kondensatora obliczamy jako sumę pól trapezów :

gdzie i = 1,2,..15 ( punkty pomiarowe ), więc całkowity ładunek obliczamy jako : , błąd bezwzględny :

ostatecznie :

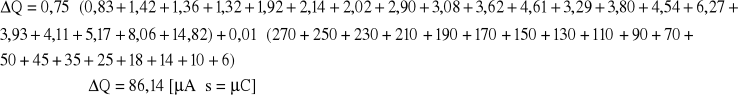
Błąd względny :

Błąd obliczeń pojemności :

bezwzględny :
ostatecznie

względny :

Wnioski:

Pojemność badanego kondensatora C = 426,41 20,63 F, stała czasowa = 14,50 s.

Wyznaczanie pojemności w sposób przedstawiony w ćwiczeniu jest dość kłopotliwe, gdyż czasochłonne jest obliczanie ładunku zgromadzonego w kondensatorze jako pola pod krzywą rozładowania I = f(t). Jak widać na rys. 1 w obwodzie rozładowania kondensatora prąd maleje asymptotycznie do 0. Teoretycznie prąd nigdy nie osiągnie wartości 0 ( w nieskończoności ), w praktyce nastąpi to po kilku stałych czasowych.

---