POMIARY IMPEDANCJI

Cel ćwiczenia

Pomiar i ocena jakości pomiaru parametrów elementów RLC stosowanych w obwodach

prądu zmiennego, a także nabycie i ukształtowanie podstawowych metod jej pomiaru.

Zagadnienia do przygotowania

1. Pojęcia: impedancja, reaktancja indukcyjna, reaktancja pojemnościowa, rezystancja, kąt przesunięcia fazowego.

2. Wpływ zmiany częstotliwości na własności parametrów elementów impedancyjnych.

3. Podstawowe własności dwójników RLC w stanie rezonansu szeregowego
   i równoległego, charakterystyki częstotliwościowe.

4. Schematy zastępcze elementów i ich interpretacja.

5. Metody pomiaru impedancji.

Literatura

1. Jelonek A. Karkowski Z.: Eksploatacja i konserwacja elektronicznych przyrządów

pomiarowych, Łódź PWN 1966

2. Łapiński M.:Miernictwo teletransmisyjne, WKiŁ Warszawa 1966

3. Kaźmierczak W.: Miernictwo teletechniczne WNT Warszawa 1971

4. J. Stanclik : Laboratorium elementów biernych i podzespołów elektronicznych

Wyd.KK. Jelenia Góra 2005 (sygn.59841)

Wiadomości wstępne

W skład układów elektronicznych wchodzą m.in. elementy takie jak: rezystory, kondensatory oraz cewki indukcyjne nazywane elementami biernymi. Właściwy dobór tych elementów oraz znajomość ich właściwości częstotliwościowych warunkują poprawną pracę całego układu elektronicznego.

W obwodach prądu zmiennego elementy bierne charakteryzują się impedancją, której wartość zespoloną zapisujemy w postaci:

gdzie: R - rezystancja (składowa czynna)
X=X_L-X_C - reaktancja (składowa bierna),
|Z| =Z = R² + X² jest modułem impedancji,
φ = arc tg X/R jest kątem fazowym impedancji.

Idealny rezystor R nie wprowadza przesunięcia fazowego, a jego impedancja jest równa rezystancji Z = R, idealny kondensator C (bezstratny) powoduje opóźnienie napięcia względem przepływającego przez niego prądu o /2, a jego impedancja równa się reaktancji pojemnościowej Z_C = jX_C; w idealnej cewce natomiast napięcie wyprzedza prąd o /2. a impedancja jest równa reaktancji indukcyjnej Z_L= jX_L.

W rzeczywistych elementach R,L,C przesunięcie fazowe φ między napięciem

i prądem różni się od wspomnianych wyżej wartości. Wynika to z istnienia parametrów resztkowych, np. pasożytniczych indukcyjności i pojemności doprowadzeń w rezystorach, indukcyjności i rezystancji doprowadzeń w kondensatorach , a w cewkach, rezystancji

i pojemności uzwojeń. Wartości niepożądanych parametrów są zależne od technologii wykonania elementów.

W zakresie częstotliwości akustycznych wpływ parametrów resztkowych jest niewielki. Staje się on istotny w zakresie wielkich częstotliwości. Właściwości podzespołów rzeczywistych, na podstawie analizy właściwości fizycznych danego elementu przedstawia się w postaci schematów zastępczych. Dla większości elementów wystarczającym jest schemat zastępczy dwuelementowy (dwójnik). Jeden z elementów stanowi parametr podstawowy, drugi natomiast reprezentuje straty związane z istnieniem elementów resztkowych. W zależności od tego, który z parametrów przedstawionego układu zastępczego jest dominujący, to wypadkowy charakter elementu może być: rezystancyjny, indukcyjny lub pojemnościowy. Z tego powodu istotne jest, aby badania elementów R, L, C odbywały się w warunkach zbliżonych do użytkowych warunków pracy.

Rezystorowi włączonemu w obwód prądu zmiennego można przyporządkować schemat zastępczy, w którym indukcyjność L doprowadzeń rezystora (oraz uzwojeń rezystorów drutowych) i pojemność C między zaciskami wejściowymi są połączone równolegle, rys. 2a. W takim przypadku rezystor będzie posiadał charakter indukcyjny, jeśli L > R² C, a pojemnościowy jeśli L < R² C. Rezystory o wartościach większych od l k (a więc większość) posiadają charakter pojemnościowy, dlatego schemat zastępczym upraszcza się do równoległego połączenia rezystancji R i pojemności C (rys. 2b).

Rezystory drutowe, na ogół o rezystancjach znamionowych mniejszych niż l k, posiadają w zakresie małych częstotliwości, charakter indukcyjny, co odpowiada szeregowemu połączeniu rezystancji i indukcyjności.

Kondensator rzeczywisty należy traktować jako dwójnik o elementach: rezystancyjnym i pojemnościowym połączonych szeregowo lub równolegle (rys. 3). Rezystory R_s i R_r, reprezentują wypadkowe straty energii w dielektryku, doprowadzeniach i okładzinach kondensatora.

Schemat zastępczy z rys.3a jest stosowany częściej dla kondensatorów o małych stratach, a schemat z rys. 3b dla kondensatorów o dużych stratach.

Wartość strat kondensatora charakteryzuje współczynnik stratności, opisywany jako tangens kąta stratności - tg δ. Jest to wartość kąta dopełniającego do 90° kąt przesunięcia fazowego φ między prądem i napięciem kondensatora. Dla szeregowego schematu zastępczego współczynnik stratności :

tg δ =R_sC_s (2)
dla równoległego schematu zastępczego

(3)

Współczynnik ten określa stopień, w jakim kondensator rzeczywisty odbiega od idealnego. Zmiana częstotliwości wywołuje zmianę współczynników stratności obu modeli. Z analizy zjawisk zachodzących w kondensatorach rzeczywistych wynika, że dla częstotliwości f < 100 kHz ich właściwości lepiej odwzorowuje układ zastępczy równoległy, zaś dla f > 100 kHz - układ zastępczy szeregowy. W rozważaniach dokładniejszych, w schemacie zastępczym kondensatora można uwzględnić: indukcyjność i rezystancję doprowadzeń oraz rezystancję strat dielektrycznych i upływności izolacji. Schemat zastępczy znacznie się komplikuje a analiza i możliwości pomiarowe znacznie przekraczają ramy tego ćwiczenia i dlatego nie będzie rozpatrywany.

Cewce indukcyjnej w zakresie małych częstotliwości i przy małej wartości indukcji pola magnetycznego można przyporządkować jeden z poniższych układów zastępczych (rys.4):

Rezystancje w tych schematach reprezentują straty omowe w przewodzie cewki, straty na prądy wirowe, straty dielektryczne pojemności rozproszonych oraz, jeśli cewka posiada rdzeń ferromagnetyczny, straty w rdzeniu wynikające głównie z prądów wirowych oraz strat histerezowych. Wszystkie straty w cewce składają się na wypadkowy współczynnik stratności, którego odwrotność jest nazywana dobrocią cewki Q i jest parametrem jakości cewki:

Pomiar impedancji, sprowadza się do określenia wartości jej składowych:

rezystancji R oraz reaktancji X lub modułu Z i kąta fazowego φ

Do podstawowych metod pomiaru impedancji zaliczamy :

metodę techniczną,

metodę mostkową

metodę rezonansową.

Metoda techniczna pomiaru impedancji Z polega na:

• pomiarze: napięcia U i prądu I za pomocą woltomierza i amperomierza,

• pomiarze mocy czynnej P za pomocą watomierza,

• obliczeniu:

• modułu, na podstawie prawa Ohma |Z| = U/I,

• argumentu φ =arc cos(P/(UI)) gdzie UI=S - moc pozorna,

• 
  składowej czynnej R=P/I²

• składowej biernej X = Z² - R²

W czasie pomiarów należy mieć na uwadze ograniczony zakres częstotliwościowy poprawnej pracy przyrządów pomiarowych, który pozwala mierzyć napięcia i prądy z zadawalającą dokładnością do ok. 100 kHz. Ograniczenie to w szczególności dotyczy to watomierzy, których częstotliwości pomiarowe ograniczone są do kilku kiloherców.

W ćwiczeniu zastosowano metodę pomiaru modułu wzorowaną na metodzie technicznej. Natomiast dla wyznaczenia elementów składowych schematu zastępczego impedancji dokonywany będzie pomiar kąta fazowego przy pomocy oscyloskopu. Dokonując pomiaru napięcia U, prądu I i kąta fazowego φ wykonujemy obliczenia:

• 
  modułu, na podstawie prawa Ohma |Z| = U/I,

• składowej czynnej R = |Z|cos φ 5

• składowej biernej X = |Z|sin φ

Dokładność pomiaru poszczególnych parametrów zależy od klas zastosowanych mierników oraz od błędów metody pomiaru kąta fazowego.

Pomiary

Zmontować układ pomiarowy wg rys. 5.

Badany będzie dwójnik zawierający szeregowe połączenie elementów R_R i L. Pomiary: napięcia na dwójniku impedancyjnym U_Z, prądu płynącego przez dwójnik I oraz kąta fazowego φ wykonujemy na podstawie zobrazowania przebiegów na ekranie oscyloskopu (rys. 6).

Dla ułatwienia i jednocześnie poprawienia dokładności pomiaru napięć zmiennych (U_Z i U_R), z ekranu oscyloskopu, odczytujemy wartości podwójnej amplitudy: U_Zp-p,U_Rp-p Wówczas moduł impedancji dwójnika indukcyjnego określa zależność:

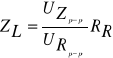
(6)

Natomiast kąt fazowy φ określa zależność pokazana na rys. 6.

Moduł impedancji |Z|, sładową czynną R oraz składową bierną X obliczamy wg (5).

Wyniki pomiarów i obliczeń umieścić w tabeli:

Pomiary					Obliczenia
f	UZp-p	URp-p	AB	AC	Z	ϕ	R	X

Pomiar kąta fazowego:

Podając dwa przebiegi na wejścia oscyloskopu ( rys.5), można określić przesunięcie faz między nimi mierząc długości odcinków: AB i AC (rys.6). Długość odcinka AC odpowiada okresowi drgań, odcinka AB zaś — przesunięciu fazowemu między dwoma napięciami. Dokładność opisywanej metody jest niewielka. Zazwyczaj należy się liczyć z uchybem nie mniejszym niż 3°.

Kolegium Karkonoskie Laboratorium miernictwa

1

Pomiary impedancji str.

Rys. 2. Schematy zastępcze rezystora

Rys. 3. Schematy zastępcze kondensatora.

Rys. 1. Składowe impedancji Z

Rys. 6. Zobrazowanie na ekranie oscyloskopu:
U_Z - napięcie na dwójniku, U_R - spadek napięcia na rezystancji R.

Rys. 5. Schemat układu pomiarowego do pomiarów impedancji dwójnika RL

U_Z

U_R

ϕ

U_Rpp-pp

U_Zp-p

R_R

b)

a)

R _r

L _r

R _s

L _s

Rys.4. Uproszczone schematy zastępcze cewki

C_r

L_r

R_s

L_s

a)

b)

---