Modele matematyczne i analiza wariancji

Analiza wariancji dla rozpatrywanych cech prowadzona jest wg następującego modelu liniowego:

W_ijkmn - wartość cechy n-tego osobnika

μ - średnia zbioru

s_i - efekt i-tego samca (buhaj, ogier, tryk, lub cap), i = 1, 2..., 4

h_j - efekt j-tego stada, j = 1, 2

y_k - efekt k-tego roku, k = 1, 2, 3

p_m - efekt m-tego sezonu, m = 1, 2

e_ijkmn - błąd losowy związany z n-tą obserwacją

Praktyczne wykonanie ćwiczenia w Ms Excel obejmuje następujące etapy:

1. Ułożenie macierzy obserwacji (liczby obserwacji)

Macierz obserwacji to tabela, w której liczba obserwacji uporządkowana jest wg następującego schematu:

μ

s1

s2

s3

s4

h1

h2

y1

y2

y3

p1

p2

μ

s1

s2

s3

s4

h1

h2

y1

y2

y3

p1

p2

Macierz wypełnia się w ten sposób, że:

• na przecięciu wartości μ i μ wpisujemy liczbę wszystkich obserwacji, czyli liczbę zwierząt łącznie, np. 110, 112 itp. Na przecięciu s1 i s1 wpisujemy liczbę potomstwa samca nr 1, na przecięciu s2 i s2 - liczbę potomstwa samca nr 2 itp., na przecięciu h1 i h1 - liczbę zwierząt występujących w stadzie nr 1.

• Natomiast na przecięciu s1 i s2 - należy wpisać 0, gdyż zwierzę nie może być jednocześnie potomkiem dwóch samców. Podobnie jest np. z przecięciem h1 i h2 ze względu na to iż zwierzę nie może być jednocześnie w stadzie nr 1 i nr 2, lub y1 i y2, ponieważ jeśli wykonaliśmy pomiar cechy w roku nr 1 to już nie wykonaliśmy go w roku nr 2 itd.

• W przypadku przecięcia wartości np. s3 i y2 wpisujemy liczbę obserwacji, która jednocześnie spełnia oba warunki, tzn. zwierzę jest potomkiem samca nr 3, a pomiar cechy wykonano dla niego w roku 2. Na przecięciu np. h2 i p1 wpisujemy liczbę obserwacji, która spełnia obydwa warunki, tzn. zwierzę pochodzi ze stada nr 2 a pomiar cechy został wykonany w sezonie nr 1.

Aby wykonać ćwiczenie wystarczy sortować odpowiednio dane, np. aby określić ile potomków ojca nr 1 występuje w stadzie 1 należy posortować dane rosnąco wg ojców, a w obrębie ojców wg stad i określić liczbę, która spełnia te dwa kryteria a następnie wpisać otrzymana wartość w macierzy na przecięciu kolumny s1 i wiersza h1, oraz wiersza s1 i kolumny h1 (w poniższym przykładzie takich obserwacji jest 11).

Można także wykorzystywać funkcję „LICZ JEŻELI” oraz wklejać wyniki obliczeń jako wartości.

2. Ułożenie wektorów danych dla każdej z cech (wektorów wartości obserwacji)

Układamy wektor danych dla każdej z trzech cech wg schematu:

	Wektor dla cechy1	Wektor dla cechy 2	Wektor dla cechy 3
μ
s1
s2
s3
s4
h1
h2
y1
y2
y3
p1
p2

Tworząc wektor dla cechy 1 wpisujemy sumy wartości cechy pierwszej, np. w wierszu oznaczonym jako μ - sumę wszystkich wartości cechy 1, w wierszu oznaczonym jako s1 - sumę wartości cechy 1 dla potomstwa samca nr 1, jako s2 - sumę wartości dla samca nr 2, w wierszu oznaczonym jako y1 - sumę wartości cechy 1 dla zwierząt, którym pomiary wykonano w roku 1 itd.

W celu prawidłowego wykonania obliczeń należy odpowiednio sortować dane i wykorzystywać funkcję SUMA wg schematów podawanych na poprzednich ćwiczeniach, oraz wklejać wyniki obliczeń jako wartości w stworzonej tabelce.

Takie same obliczenia należy przeprowadzić dla cechy nr 2 i nr 3.

3. Redukowanie macierzy obserwacji

Aby zredukować macierz obserwacji należy stworzyć nową tabelkę i na podstawie pierwotnej macierzy obserwacji dokonać następujących obliczeń najpierw w obrębie kolumn:

	μ	s1	s2	s3	h1	y1	y2	p1
μ	μ	s1-s4	s2-s4	s3-s4	h1-h2	y1-y3	y2-y3	p1-p2
s1	s1	s1-s4	s2-s4	s3-s4	h1-h2	y1-y3	y2-y3	p1-p2
s2	s2	s1-s4	s2-s4	s3-s4	h1-h2	y1-y3	y2-y3	p1-p2
s3	s3	. . .	. . .	. . .	. . .	. . .	. . .	. . .
s4	s4	. . .	. . .	. . .	. . .	. . .	. . .	. . .
h1	h1	. . .	. . .	. . .	. . .	. . .	. . .	. . .
h2	h2	. . .	. . .	. . .	. . .	. . .	. . .	. . .
y1	y1	. . .	. . .	. . .	. . .	. . .	. . .	. . .
y2	y2	. . .	. . .	. . .	. . .	. . .	. . .	. . .
y3	y3	. . .	. . .	. . .	. . .	. . .	. . .	. . .
p1	p1	. . .	. . .	. . .	. . .	. . .	. . .	. . .
p2	p2	. . .	. . .	. . .	. . .	. . .	. . .	. . .

Wartości napisane grubą czcionką brane są do obliczeń z pierwotnej macierzy obserwacji.

Po wykonaniu obliczeń kolumnami, redukcję wykonuje się wierszami w oparciu o nowo powstałą macierz:

	μ	s1	s2	s3	h1	y1	y2	p1
μ	μ	s1	s2	s3	h1	y1	y2	p1
s1	s1-s4	s1-s4	. . .	. . .	. . .	. . .	. . .	. . .
s2	s2-s4	s2-s4	. . .	. . .	. . .	. . .	. . .	. . .
s3	s3-s4	s3-s4	. . .	. . .	. . .	. . .	. . .	. . .
h1	h1-h2	h1-h2	. . .	. . .	. . .	. . .	. . .	. . .
y1	y1-y3	y1-y3	. . .	. . .	. . .	. . .	. . .	. . .
y2	y2-y3	y2-y3	. . .	. . .	. . .	. . .	. . .	. . .
p1	p1-p2	p1-p2	. . .	. . .	. . .	. . .	. . .	. . .

Wartości napisane grubą czcionką brane są do obliczeń z macierzy obserwacji zredukowanej kolumnami.

4. Redukcja wektorów danych (wektorów obserwacji)

Wektory redukowane są wierszami wg poniższego schematu:

	Wektor dla cechy1	Wektor dla cechy 2	Wektor dla cechy 3
μ	μ1	μ2	μ3
s1	s1-s4	s1-s4	s1-s4
s2	s2-s4	s2-s4	s2-s4
s3	s3-s4	s3-s4	s3-s4
h1	h1-h2	h1-h2	h1-h2
y1	y1-y3	y1-y3	y1-y3
y2	y2-y3	y2-y3	y2-y3
p1	p1-p2	p1-p2	p1-p2

Wartości napisane grubą czcionką brane są do obliczeń z pierwotnych wektorów danych.

5. Odwracanie macierzy obserwacji

Zredukowana macierz obserwacji powinna być kwadratowa (8 wierszy na 8 kolumn) i symetryczna. Odwracanie jej prowadzone jest wg schematu przedstawionego w konspekcie I pt. „Macierze”.

6. Obliczanie wektorów stałych

Aby otrzymać wartości stałe, czyli spełniające równania (patrz „rozwiązanie modelu liniowego metodą najmniejszych kwadratów” - np. wykład lub załączone materiały - str. 75), mnożymy odwróconą macierz obserwacji przez każdy ze zredukowanych wektorów danych osobno. Wynikiem będą więc trzy wektory stałych.

Działanie mnożenia dwóch macierzy wykonywane jest wg schematu przedstawionego w konspekcie I pt. „Macierze”.

Modele matematyczne i analiza wariancji c.d.

7. Analiza wariancji dla poszczególnych cech.

Wyniki dalszych obliczeń zamieszczone będą w tabelach skonstruowanych dla poszczególnych cech wg poniższego schematu (każda cecha ma osobną tabelę):

Źródło zmienności	df (liczba stopni swobody)	SS ( suma kwadratów)	MS ( średni kwadrat)	k	Komponent wariancji
Efekt samca	Liczba samców - 1	Wyjaśnienie w punkcie 8 kon-spektu	SS samca / df samca	Wyjaśnienie w punkcie 10 ko-nspektu	(MS samca - MS błędu) / k dla samca
Efekt stada	Liczba stad - 1	Wyjaśnienie w punkcie 8 kon-spektu	SS stada / df stada	Wyjaśnienie w punkcie 10 ko-nspektu	(MS stada - MS błędu) / k dla stada
Efekt roku	Liczba lat - 1	Wyjaśnienie w punkcie 8 kon-spektu	SS roku / df roku	Wyjaśnienie w punkcie 10 ko-nspektu	(MS roku - MS błędu) / k dla roku
Efekt sezonu	Liczba sezonów - 1	Wyjaśnienie w punkcie 8 kon-spektu	SS sezonu / df sezonu	Wyjaśnienie w punkcie 10 ko-nspektu	(MS sezonu - MS błędu) / k dla sezonu
Błąd	Liczba obserwacji - df samców - df stad - df lat - df sezonów - 1	Wyjaśnienie w punkcie 9 kon-spektu	SS błędu / df błędu

8. Obliczanie sumy kwadratów dla poszczególnych efektów głównych, tzn. samca, stada, roku i sezonu.

Aby obliczyć sumę kwadratów dla samca należy:

• Wyznaczyć macierze obserwacji i wektory stałych dla poszczególnych efektów głównych. Poniższy schemat przedstawia które elementy macierzy obserwacji i wektorów stałych odpowiadają poszczególnym efektom.

• Aby obliczyć sumę kwadratów dla cechy I dla efektu samca, należy:

• transponować wycinek wektora stałych cechy I odpowiadający efektowi samca

• odwrócić wycinek odwróconej już macierzy obserwacji, odpowiadający efektowi samca

• pomnożyć transponowany wycinek wektora stałych przez odwrócony wycinek odwróconej macierzy obserwacji, a otrzymany wynik pomnożyć przez wycinek wektora stałych przed transponowaniem (odpowiadający efektowi samca). Efektem będzie jedna liczba, która jest sumą kwadratów dla efektu samca dla cechy I.

• Aby obliczyć dla efektu samca sumy kwadratów dla cechy II i III, należy posłużyć się tym samym fragmentem macierzy obserwacji ale wykorzystać odpowiednie wycinki wektorów stałych dla cechy II i III. Schemat obliczeń jest taki sam.

• Podobny schemat postępowania zastosować dla efektu stada, roku i sezonu posługując się odpowiednimi wycinkami macierzy i wektorów stałych.

• Wyniki wpisywać do wynikowej tabeli analizy wariancji dla cechy I, II i III.

9. Obliczenie sumy kwadratów dla błędu

Aby obliczyć sumę kwadratów dla błędu korzystamy ze wzoru:

W tym celu trzeba dokonać obliczenia dwóch wartości:

• Ogólna suma kwadratów dla danej cechy
  :

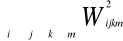
Ogólną sumę kwadratów np. dla cechy I obliczamy podnosząc każdą wartość cechy I do kwadratu i sumując wszystkie otrzymane wartości. W programie MsExcel wykonać to można wykorzystując gotową formułę „POTĘGA”. Wg poniższego schematu

Po podniesieniu do kwadratu pierwszej wartości, przeciągamy (kopiujemy) formułę na pozostałe komórki dla cechy I, a następnie otrzymane wartości sumujemy z wykorzystaniem formuły „SUMA”.

Podobnie postępujemy z cechą II i III.

• Poprawka R
  :

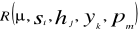
Aby otrzymać wartość R dla cechy I mnożymy wektor stałych dla tej cechy przez zredukowany wektor obserwacji dla cechy I. Aby było to możliwe należy najpierw wykonać transponowanie wektora stałych. Transponowanie wektora stałych dla cechy I wykonuje się w ten sposób, że kopiujemy wektor, a następnie w wolnym wierszu zaznaczamy komórkę i używamy opcji „wklej specjalnie”. Po rozwinięciu okna zaznaczmy ptaszkiem „transpozycja” jak na rysunku poniżej:

Transponowany wektor stałych mnożymy przez wektor obserwacji wg znanego schematu mnożenia dwóch macierzy (instrukcja w konspekcie o macierzach). Wynikiem mnożenia dwóch wektorów jest jedna liczba.

• Otrzymaną poprawkę R odejmujemy od ogólnej sumy kwadratów i w ten sposób otrzymujemy
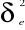
  - sumę kwadratów dla błędu dla cechy I.

• Podobnie postępujemy z cechą drugą i trzecią.

Modele matematyczne i analiza wariancji c.d.

10. Obliczanie współczynnika „k” dla oszacowania komponentów wariancji

Aby obliczyć współczynnik „k” dla wybranego efektu trzeba skorzystać z powtórnie odwróconego fragmentu macierzy dla tego efektu. Np. żeby policzyć k dla efektu samca należy:

• Wykorzystać odwrócony wycinek odwróconej macierzy obserwacji, odpowiadający efektowi samca,

• Zsumować wartości leżące na przekątnej tej macierzy (załóżmy, że wynik działania oznaczymy jako „A”),

• Zsumować wartości leżące poza przekątną macierzy (załóżmy, że wynik działania oznaczymy jako „B”),

• Wartość B podzielić przez liczbę stopni swobody dla efektu samca, tzw. df samca (załóżmy, że wynik działania oznaczymy jako „C”),

• Odjąć wynik działania oznaczony jako C od wyniku oznaczonego jako A (załóżmy, ze wynik działania oznaczymy jako D = A-C),

• Podzielić wynik oznaczony jako D przez liczbę samców (wynikiem jest współczynnik „k” dla efektu samca)

• Podobny schemat postępowania przyjąć przy obliczaniu współczynników „k” dla stada, roku, i sezonu

Adres pierwszej wartości cechy I

Wykładnik potęgi do której ma być podniesiona liczba

---