Przykład rozwiązania układu równań metodą eliminacji Gaussa

Metodą eliminacji Gaussa rozwiąż układ równań

.

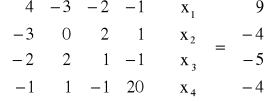
Zapisujemy układ w tabelce i realizujemy postępowanie proste. Polega ono na tym, że dla kolejnych wartości i = 1, 2, 3, 4

a) poniżej wiersza kierującego (tzn. wiersza nr i) i na prawo od kolumny kierującej (tzn. kolumny nr i) stosujemy regułę prostokąta, czyli a_j,k zastępujemy przez a_j,k - a_j,i⋅a_i,k/a_i,i,

b) wiersz kierujący dzielimy przez element kierujący (jest nim a_i,i),

c) pod element kierujący wpisujemy zera.

Poniżej pokazane są etapy postępowania prostego dla i = 1, 2, 3. Początkowe wiersze tabelki oznaczone są przez {A1}, {A2}, {A3}, {A4}. W wyniku operacji wykonanych przy i = 1 stają się one wierszami odpowiednio {B1}, {B2}, {B3}, {B4} i na przykład zapis

{B3} = {A3}+2⋅{B1} oznacza, że wiersz {B3} powstaje przez odjęcie od wiersza {A2} wiersza {B1} pomnożonego przez (-3), gdyż (-3) jest tym elementem wiersza {A2}, który zostaje zastąpiony przez 0.

Nie jest pokazany etap ostatnim, tj. dla i = 4, ponieważ dla podanej macierzy sprowadza się on do podzielenia wiersza {D4} przez 1, a więc nie zmienia wierszy {D1}-{D4}.

wiersz	⋅x1	⋅x2	⋅x3	⋅x4	⋅1
{A1}	4	-3	-2	-1	9
{A2}	-3	0	2	1	-4
{A3}	-2	2	1	-1	-5
{A4}	-1	1	-1	20	-4
{B1} = {A1}/4	1	-3/4	-1/2	-1/4	9/4
{B2} = {A2}+3⋅{B1}	0	-9/4	1/2	1/4	11/4
{B3} = {A3}+2⋅{B1}	0	1/2	0	-3/2	-1/2
{B4} = {A4}+1⋅{B1}	0	1/4	-3/2	79/4	-7/4
{C1} = {B1}	1	-3/4	-1/2	-1/4	9/4
{C2} = {B2}/(-9/4)	0	1	-2/9	-1/9	-11/9
{C3} = {B3}-1/2⋅{C1}	0	0	1/9	-13/9	1/9
{C4} = {B4}-1/4⋅{C1}	0	0	-13/9	178/9	-13/9
{D1} = {C1}	1	-3/4	-1/2	-1/4	9/4
{D2} = {C2}	0	1	2/9	-1/9	-11/9
{D3} = {C3}/(-1/9)	0	0	1	-13	1
{D4} = {C4}+13/9⋅{D3}	0	0	0	1	0

Postępowanie proste zostało zakończone. Realizujemy postępowanie odwrotne:

wiersz {D4} to równanie 1⋅x₄ = 0, skąd od razu x₄ = 0.

wiersz {D3} to równanie 1⋅x₃ -13⋅x₄ = 1, a więc x₃ = 1 + 13⋅0 = 1.

wiersz {D2} to równanie 1⋅x₂ +2/9⋅x₃ -1/9⋅x₄ = -11/9,

a więc x₂ = -11/9 -2/9⋅1 -1/9⋅0 = -1.

Wiersz {D1} to równanie 1⋅x₁ -3/4⋅x₂ -1/2⋅x₃ -1/4⋅x₄ = 9/4,

zatem x₁ = 9/4 +3/4⋅(-1) +1/2⋅1 +1/4⋅0 = 3.

Przykład wyznaczania macierzy odwrotnej stosujący regułę prostokąta

Wyznacz macierz odwrotną do macierzy

A = 

Rozwiązanie.

Wykonujemy kolejno przekształcenia (stosując regułę prostokąta nie tylko do wyrazów znajdujących się poniżej wiersza rozwiązującego, lecz także powyżej tego wiersza):

wiersz
{A1}	1	2	3	4	1	0	0	0
{A2}	2	5	6	7	0	1	0	0
{A3}	3	6	8	9	0	0	1	0
{A4}	4	7	9	9	0	0	0	1
{B1}={A1}/1	1	2	3	4	1	0	0	0
{B2}={A2}-2⋅{B1}	0	1	0	-1	-2	1	0	0
{B3}={A3}-3⋅{B1}	0	0	-1	-3	-3	0	1	0
{B4}={A4}-4⋅{B1}	0	-1	-3	-7	-4	0	0	1
{C1}={B1}-2⋅{C2}	1	0	3	6	5	-2	0	0
{C2}={B2}/1	0	1	0	-1	-2	1	0	0
{C3}={B3}-0⋅{C2}	0	0	-1	-3	-3	0	1	0
{C4}={B4}+1⋅{C2}	0	0	-3	-8	-6	1	0	1
{D1}={C1}-3⋅{D3}	1	0	0	-3	-4	-2	3	0
{D2}={C2}-0⋅{D3}	0	1	0	-1	-2	1	0	0
{D3}={C3}/(-1)	0	0	1	3	3	0	-1	0
{D4}={C4}+3⋅{D3}	0	0	0	1	3	1	-3	1
{E1}={D1}+3⋅{E4}	1	0	0	0	5	1	-6	3
{E2}={D2}+1⋅{E4}	0	1	0	0	1	2	-3	1
{E3}={D3}-3⋅{E4}	0	0	1	0	-6	-3	8	-3
{E4}={D4}/1	0	0	0	1	3	1	-3	1

Na miejscu macierzy danej uzyskaliśmy macierz jednostkową, zaś na miejscu macierzy jednostkowej - macierz odwrotną do danej. Tak więc macierz odwrotna to

A^-1 = 
.

Postępowanie w przypadku, gdy element kierujący jest równy 0

Jeśli w trakcie realizacji metody eliminacji Gaussa lub odwracania macierzy pojawia się element kierujący a_i,i = 0, to

1. jeśli każdy element poniżej niego znika (tj. a_j,i = 0 dla j > i), to macierz jest osobliwa,

2. jeśli istnieje jakiś a_j,i ≠ 0 z j > i, to przestawiamy wiersze j-ty z i-tym i kontynuujemy postępowanie, pamiętając, że w końcowym wyniku musimy dokonać odpowiedniego przestawienia

Na przykład dla wierszy A1 = [1, 1, 1],

A2 = [2, 1, 1],

A3 = [3, 3, 1]

macierzy A = 
=
=: A(1,2,3)

i kolumn Z1 =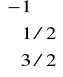
, Z2 =
, Z3 =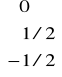

macierzy Z =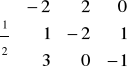 
= [Z1 Z2 Z3 ] =: Z(1,2,3)

mamy A(1,2,3)^-1 = Z(1,2,3),

A(2,1,3)^-1 = Z(2,1,3),

A(3,2,1)^-1 = Z(3,2,1) itd.

Zaobserwowaną własność wyrażamy zdaniem: odwrotność macierzy, której wiersze zostały przestawione, jest odwrotnością macierzy wyjściowej o odpowiednio przestawionych kolumnach:

jeśli A(1,2,...,n)^-1 = Z(1, 2,..., n), to dla każdej permutacji p = (p₁, p₂, ..., p_n) wierszy macierzy A zachodzi wzór A(p₁, p₂, ..., p_n)^-1 = Z(p₁, p₂, ..., p_n).

Inaczej możemy powiedzieć: odwracanie macierzy jest (w sensie przyjętym powyżej) niezmiennicze ze względu na permutację jej wierszy. Własność ta pozostaje prawdziwa także w odniesieniu do kolumn.

Realizacja w systemie DERIVE

Realizacja pełnej eliminacji wykonanej w macierzy A na elemencie znajdującym się w wierszu nr j i kolumnie nr k w programie Derive for Windows sprowadza się do symplifikacji napisu wywołującego funkcję

fullPivot(a, j, k) := VECTOR( IF(j_=j, a_j /a_j,k, a_j_-a_{j_,k} /a_j,k·a_j), j_, DIM(a)).

Przykład pracy tej funkcji pokazuje screenshot. Dla szybszego utworzenia macierzy roszerzającej daną macierz a o macierz jednostkową warto korzystać z funkcji

glueMatrices(A, B) := VECTOR( APPEND(A_j, B_j), j, DIM(A)),

glueWithIdentityMatrix(A) := glueMatrices(A, IDENTITY_MATRIX(DIM(A))).

Realizacja eliminacji obejmującej jedynie elementy poniżej wiersza kierującego (nr i) i na prawo od kolumny kierującej (nr i), czyli - jak mówimy - wykonywanej na elemencie a_j,i - to symplifikacja napisu wywołującego funkcję

rectangularRule(a,i):=changeInVector(PIVOT(i,i,i),i,a_i/a_i,i),

w którym korzysta się z funkcji

changeInVector(v, j, a) := VECTOR( IF (j_=j, a, v_{j_}), j_, DIM(v))

zastępującej w wektorze v element nr j przez a.

Adam Marlewski, 21.XI.2005.

MEG.doc Metoda eliminacji Gaussa 3/4

---