Politechnika Gdańska Rok akademicki 1999/2000
Wydział Budownictwa Lądowego

LABORATORIUM Z MECHANIKI BUDOWLI I WYTRZYMAŁOŚCI MATERIAŁÓW
Ćwiczenie nr 12
Temat: Skręcanie swobodne pręta o przekroju
pierścieniowym zamkniętym i otwartym
Aleksander Semczuk
Bartłomiej Rysak
Michał Rzodkiewicz
Skręcaniem nazywamy przypadek, gdy w przekroju poprzecznym występuje tylko moment skręcający. Skręcanie swobodne (inaczej czyste, lub skręcanie Saint Venanta), charakteryzuje się istnieniem tylko naprężeń stycznych w przekroju.
Doświadczenie 1: Skręcanie pręta o przekroju pierścieniowym zamkniętymi
W doświadczeniu, na początku obciążono pręt momentem skręcającym Mo = Pro poprzez przyłożenie siły P = 1 kg na ramieniu początkowym ro. Następnie dokonano odczytów początkowych czujników zegarowych, po czym pręt obciążono ponownie momentem skręcającym M1 = Pr1 poprzez przyłożenie siły P = 1 kg na ramieniu r1.
Seria odczytów |
Nr punktu |
1 |
2 |
Odczyt I |
OP |
4,81 |
2,01 |
|
OK. |
4,69 |
1,98 |
|
δ [m] |
0,12 |
0,03 |
Odczyt II |
OP |
4,80 |
2,01 |
|
OK. |
4,70 |
1,99 |
|
δ [m] |
0,10 |
0,02 |
Odczyt III |
OP |
4,83 |
2,01 |
|
OK. |
4,70 |
1,99 |
|
δ [m] |
0,13 |
0,02 |
|
δśr |
0,12 |
0,02 |
|
δobl |
|
|
|
Błąd [%] |
|
|
Obliczenia:
P = 1 kg = 9,80665N ≈ 9,81 N
ro = 0,20 m
MS0 = 0,20 ⋅ 9,81 = 1,962 Nm
r1 = 0,40 m
MS1 = 0,40 ⋅ 9,81 = 3,924 Nm
r2 = 0,50 m
MS2 = 0,50 ⋅ 9,81 = 4,905 Nm
r3 = 0,60 m
MS3 = 0,60 ⋅ 9,81 = 5,886 Nm
r4 = 0,70 m
MS4 = 0,70 ⋅ 9,81 = 6,867 Nm
6) r5 = 0,80 m
MS5 = 0,80 ⋅ 9,81 = 7,848 Nm
Przyrost momentów skręcających:
![]()
Kąty skręcenia (lewe):
![]()
![]()
![]()
![]()
![]()
![]()
Kąty skręcenia (prawe):
![]()
![]()
![]()
![]()
![]()
![]()
Obliczenia teoretyczne:
Wzór ogólny:
![]()
![]()
Wzór dla przekrojów zamkniętych:
![]()
As
δ
38 mm
Dane:
G = 35000 MPa = 35 ⋅ 109 Pa = 35 ⋅ 109 Pa
ΔM = 0,981 Nm
As = Π ⋅ R2 = 0,00113354 m2
σ = 1 mm = 0,1 cm = 0,001 m
R = 19 mm = 1,9 cm = 0,019 m
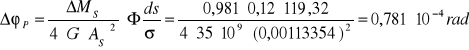
Porównanie wyników z doświadczenia z obliczeniami teoretycznymi:
Błędy lewych odczytów:
A = (Q1 + Q2 + Q3 + Q4 + Q5 + Q6) / 6 = (1,08 + 1,02 +1,01 + 0,95 + 0,92 + 0,88) / 6 = 0,9767 [mm]
Błędy bezwzględne poszczególnych pomiarów:
ΔQ1 = |A - Q1| = 0,1033
ΔQ2 = |A - Q1| = 0,0433
ΔQ3 = |A - Q1| = 0,0033
ΔQ4 = |A - Q1| = 0,0266
ΔQ5 = |A - Q1| = 0,0566
ΔQ6 = |A - Q1| = 0,0966
ΔQ = 0,0659
Błędy prawych odczytów:
A = (Q1 + Q2 + Q3 + Q4 + Q5 + Q6) / 6 = (0,06 + 0,05 +0,04 + 0,03 + 0,02 + 0,00) / 6 = 0,0333 [mm]
Błędy bezwzględne poszczególnych pomiarów:
ΔQ1 = |A - Q1| = 0,0266
ΔQ2 = |A - Q1| = 0,0166
ΔQ3 = |A - Q1| = 0,0066
ΔQ4 = |A - Q1| = 0,0033
ΔQ5 = |A - Q1| = 0,0133
ΔQ6 = |A - Q1| = 0,0333
ΔQ = 0,0997
Kąt skręcania ϕ w punkcie - wartość doświadczalna:
L = 5 ⋅ 10-4 rad
P = 1,2 ⋅ 10-4 rad
Kąt skręcania ϕ w punkcie - wartość teoretyczna:
L = 2,60 ⋅ 10-4 rad
P = 0,781 ⋅ 10-4 rad
Błędy pomiaru:
ΔL = 1,400 ⋅ 10-4 rad
ΔP = 0,419 ⋅ 10-4 rad
Doświadczenie 2: Skręcanie pręta o przekroju pierścieniowym otwartym
W doświadczeniu, na początku obciążono pręt momentem skręcającym Mo = Pro poprzez przyłożenie siły P = 1 kg na ramieniu początkowym ro. Następnie dokonano odczytów początkowych czujników zegarowych, po czym pręt obciążono ponownie momentem skręcającym M1 = Pr1 poprzez przyłożenie siły P = 1 kg na ramieniu r1.
Seria odczytów |
Nr punktu |
1 |
2 |
Odczyt I |
OP |
3,90 |
9,20 |
|
OK. |
3,82 |
8,80 |
|
δ [m] |
0,08 |
0,40 |
Odczyt II |
OP |
3,92 |
9,25 |
|
OK. |
3,82 |
8,82 |
|
δ [m] |
0,10 |
0,43 |
Odczyt III |
OP |
3,89 |
9,21 |
|
OK. |
3,81 |
8,77 |
|
δ [m] |
0,08 |
0,34 |
|
δśr |
0,09 |
0,39 |
|
δobl |
|
|
|
Błąd [%] |
|
|
Obliczenia:
P = 1 kg = 9,80665N ≈ 9,81 N
ro = 0,13 m
MS0 = 0,13 ⋅ 9,81 = 1,275 Nm
r1 = 0,15 m
MS1 = 0,15 ⋅ 9,81 = 1,471 Nm
r2 = 0,17 m
MS2 = 0,17 ⋅ 9,81 = 1,667 Nm
r3 = 0,20 m
MS3 = 0,20 ⋅ 9,81 = 1,962 Nm
r4 = 0,23 m
MS4 = 0,23 ⋅ 9,81 = 2,256 Nm
6) r5 = 0,26 m
MS5 = 0,26 ⋅ 9,81 = 2,551 Nm
Przyrost momentów skręcających:
Kąty skręcania (lewe):
Kąty skręcania (prawe):
Obliczenia teoretyczne:
Wzór ogólny:
w którym:
![]()
Dane:
G = 35 ⋅ 109 N/m2
R = 0,019 m
δ = 0,001 m
dla l1 = 0,1 m
dla l2 = 0,5 m
Porównanie wyników doświadczenie z obliczeniami teoretycznymi:
Błędy lewych odczytów:
A = (Q1 + Q2 + Q3 + Q4 + Q5 + Q6) / 6 = (10,11 + 10,08 +9,94 + 9,91 + 9,91 + 9,91) / 6 = 9,9767 [mm]
Błędy bezwzględne poszczególnych pomiarów:
ΔQ1 = |A - Q1| = 0,1333
ΔQ2 = |A - Q1| = 0,1033
ΔQ3 = |A - Q1| = 0,0366
ΔQ4 = |A - Q1| = 0,0666
ΔQ5 = |A - Q1| = 0,0666
ΔQ6 = |A - Q1| = 0,0666
ΔQ = 0,0788
Błędy prawych odczytów:
A = (Q1 + Q2 + Q3 + Q4 + Q5 + Q6) / 6 = (3,07 + 2,94 + 2,24 + 1,71 + 0,91 + 0,21) / 6 = 1,8467 [mm]
Błędy bezwzględne poszczególnych pomiarów:
ΔQ1 = |A - Q1| = 1,2233
ΔQ2 = |A - Q1| = 1,0933
ΔQ3 = |A - Q1| = 0,3933
ΔQ4 = |A - Q1| = 0,1366
ΔQ5 = |A - Q1| = 0,9366
ΔQ6 = |A - Q1| = 1,6366
ΔQ = 0,9038
Kąt skręcania ϕ w punkcie - wartość doświadczalna:
L = 4 ⋅ 10-4 rad
P = 5,72 ⋅ 10-3 rad
Kąt skręcania ϕ w punkcie - wartość teoretyczna:
L = 0,06692 rad
P = 0,01338 rad
Błędy pomiaru:
ΔL = 665,2 ⋅ 10-4 rad
ΔP = 128,08 ⋅ 10-4 rad
Wyniki badań i obliczonych teoretycznie kątów skręcenia nie pokrywają się w pełni. Przyczyną tego na pewno jest niedokładność przeprowadzonych odczytów , co wynika między innymi z wadliwego sposobu działania zegarów.
Na podstawie wyników obliczeń teoretycznych widać , że kąt skręcenia w przekrojach otwartych jest znacznie większy od kąta skręcenia w przekrojach zamkniętych , pomimo tego , iż momenty skręcające w przypadku drugim były dużo większe ( ramię i siła większe).
1
5
![]()
![]()
![]()
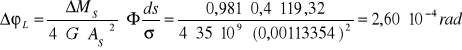
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
14 Skręcanie swobodne pręta sprawozdanie
Mechanika Budowli II - Laboratorium (rok III), Skręcanie swobodne pręta o przekroju (4), Opis doświa
Skręcanie swobodne pręta o przekroju (1), BUDOWNICTWO, INŻ, semestr 4, Mechanika budowli, Mechanika
Mechanika Budowli II - Laboratorium (rok III), Skręcanie swobodne pręta o przekroju (3), GDAŃSK 12
Skręcanie swobodne pręta o przekroju (1)1
Skręcanie swobodne pręta o przekroju (3), BUDOWNICTWO, INŻ, semestr 4, Mechanika budowli, Mechanika
Mechanika Budowli II - Laboratorium (rok III), Skręcanie swobodne pręta o przekroju (1), Politechnik
SKRĘCANIE SWOBODNE PRĘTA O PRZEKROJU
14.B PorĂłwnanie modeli, Pedagogika, Metodyka nauczania przedmiotów pedagogicznych
cw 9, Metody doświadczalne
13 WYZNACZENIE ŚRODKA ZGINANIA b, Budownictwo PG, sem4, MDwAK, Metody doświadczalne w analizie konst
9 Skrecanie Swobodne id 48098 Nieznany (2)
więcej podobnych podstron