Wydział: FTiMK |
Imię i Nazwisko: Marcin Wiśniowski |
Nr. Zespołu 5 |
Ocena Ostateczna |
Grupa: Druga |
Tytuł ćwiczenia: Wyznaczanie modułu sztywności G metodą dynamiczną |
Nr. Ćwiczenia 27 |
Data Wykonania: 22.11.2002 |
Wprowadzenie
Ciała stałe poddawane działaniu niezrównoważonych sił lub momentów sił ulegają odkształceniom. Jeżeli po usunięciu siły ciało odzyskuje pierwotny rozmiar i kształt, mówimy o jego właściwościach sprężystych.
Naprężenie mechaniczne pojawiające się w materiale jednorodnym, pochodzące od sił oddziaływania międzycząsteczkowego, równoważy siły zewnętrzne wywołujące odkształcenie materiału. Jeżeli kierunek sił odkształcających jest prostopadły do powierzchni ciała, to mówimy wtedy o naprężeniu normalnym σ, które określamy jako stosunek siły normalnej Fn do pola powierzchni S:
σ = (Fn / S)
Naprężenie nazywamy stycznym lub ścinającym, gdy działająca siła jest styczna do powierzchni. Jeżeli wartości sił działających na ciało są dostatecznie małe, to przesunięcie względne poszczególnych punktów materiału, czyli odkształcenie sprężyste, jest do nich proporcjonalne. Własność ta nosi nazwę prawa Hooke'a. Prawo Hooke'a zapisane dla naprężeń normalnych i obejmujące naprężenia dodatnie (ściskanie) i ujemne (rozciąganie) ma postac:
σ = Eε ,
gdzie miarą odkształcenia: ε = Δl/l jest wydłużenie względne. Współczynnik proporcjonalności E nazywa się modułem Younga. Prawo Hooke'a dla naprężeń stycznych wyraża się wzorem:
τ = Gα
gdzie odkształceniem względnym jest w tym wypadku kąt ścinania α. Współczynnik proporcjonalności G nazywa się modułem sztywności. Moduł ten (jak również E) jest dla danego materiału zależny od temperatury.
Jak wynika z teorii sprężystości, za pomocą tych dwóch niezależnych stałych można określić wszystkie własności sprężyste jednorodnego i izotropowego ciała. Na przykład przy zginaniu belki mamy do czynienia z czystym rozciąganiem i czystym ściskaniem opisywanym przez moduł E.
Moduł G charakteryzuje odkształcenia powstające przy skręcaniu pręta, ponieważ każdy element skręcanego drutu ulega odkształceniu typu prostego ściskania. Jeżeli jeden koniec cylindrycznego pręta o długości l i promieniu r jest zamocowany nieruchomo, a drugi skręcony o kąt φ, to wartość momenty sił sprężystych M pręta, dążącego do przywrócenia równowagi, jest proporcjonalna do kąta skręcenia φ, a stała proporcjonalności zależy od długości pręta, jego promienia oraz własności materiału:
![]()
.
Powyższy wzór jest dogodny do wyznaczania modułu sztywności G. Metoda statyczna polegałaby na pomiarze wielkości występujących we wzorze. W metodzie dynamicznej wyznacza się moduł sztywności z pomiaru okresu drgań wahadła torsyjnego. W tym celu pręt, którego moduł sztywności G mamy wyznaczyć, zawieszamy pionowo, a na jego końcu umieszczamy symetryczne ciało o znanym momencie bezwładności I. Gdy drut skręcimy i puścimy swobodnie, wibrator na jego końcu wykonuje drgania torsyjne, opisywane zgodnie z drugą zasadą dynamiki dla ruchu obrotowego równaniem:
![]()
I - moment bezwładności wibratora
![]()
- wektor przyspieszenia kątowego
M - wektor momentu sił działających na pręt
Równanie ruchu względem osi obrotu przechodzącej przez oś pręta ma postać równania oscylatora harmonicznego:
![]()
![]()
Gdzie wartość momentu kierującego: D=Gπr4/2l , a częstość drgań tego ruchu ω spełnia warunek: ω2=D/I.
Pręt wykonuje zatem drgania harmoniczne o okresie:
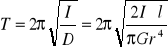
Mierząc okres T wahadła o momencie bezwładności I można wyznaczyć moduł sztywności G pręta.
Tabele Pomiarowe
Tabela 1.
Rodzaj pręta |
l [m] |
2r [m] |
4m [kg] |
2R [m] |
d [m] |
φ [m] |
t0 [s] |
t1 [s] |
|
Mosiądz |
1 |
75,3*10-2 |
2,45*10-3 |
296,74*10-3 |
4,00*10-2 |
20,21*10-2 |
4,97*10-3 |
23,8 |
34,8 |
|
2 |
|
2,46*10-3 |
|
4,01*10-2 |
20,37*10-2 |
4,97*10-3 |
24,0 |
35,0 |
|
3 |
|
2,45*10-3 |
|
4,00*10-2 |
20,13*10-2 |
4,96*10-3 |
24,6 |
35,2 |
|
4 |
|
2,45*10-3 |
|
4,01*10-2 |
20,26*10-2 |
5,05*10-3 |
24,2 |
35,6 |
|
5 |
|
2,46*10-3 |
|
4,00*10-2 |
20,23*10-2 |
4,97*10-3 |
23,8 |
35,2 |
|
6 |
|
2,46*10-3 |
|
4,00*10-2 |
20,22*10-2 |
5,03*10-3 |
24,6 |
35,2 |
|
7 |
|
2,48*10-3 |
|
4,00*10-2 |
20,28*10-2 |
4,98*10-3 |
24,6 |
35,8 |
|
8 |
|
2,45*10-3 |
|
4,00*10-2 |
20,32*10-2 |
4,97*10-3 |
24,2 |
35,4 |
|
9 |
|
2,45*10-3 |
|
4,01*10-2 |
20,28*10-2 |
4,97*10-3 |
24,2 |
35,4 |
|
10 |
|
2,45*10-3 |
|
4,00*10-2 |
20,26*10-2 |
4,97*10-3 |
24,2 |
35,2 |
|
|
r= 1,23*10-3 |
m= 74,19*10-3 |
R= 2,00*10-2 |
d= 20,26*10-2 |
φ= 4,98*10-3 |
T0=t0/30 0,81 |
T1=t1/30 1,18 |
|
|
Δl= 0,05*10-2 |
Sr= 0,002*10-3 |
Δm= 0,003*10-3 |
SR= 0,001*10-2 |
Sd= 0,02*10-2 |
Sφ= 0,01*10-3 |
ST0= 0,003 |
ST1= 0,003 |
|
Rodzaj pręta |
l [m] |
2r [m] |
4m [kg] |
2R [m] |
d [m] |
φ [m] |
t0 [s] |
t1 [s] |
|
Stal |
1 |
74,5*10-2 |
2,00*10-3 |
296,74*10-3 |
4,00*10-2 |
20,21*10-2 |
4,97*10-3 |
27,2 |
39,6 |
|
2 |
|
1,99*10-3 |
|
4,01*10-2 |
20,37*10-2 |
4,97*10-3 |
27,4 |
39,8 |
|
3 |
|
1,99*10-3 |
|
4,00*10-2 |
20,13*10-2 |
4,96*10-3 |
26,8 |
39,0 |
|
4 |
|
1,97*10-3 |
|
4,01*10-2 |
20,26*10-2 |
5,05*10-3 |
26,8 |
38,8 |
|
5 |
|
1,99*10-3 |
|
4,00*10-2 |
20,23*10-2 |
4,97*10-3 |
27,8 |
39,2 |
|
6 |
|
1,98*10-3 |
|
4,00*10-2 |
20,22*10-2 |
5,03*10-3 |
27,6 |
39,4 |
|
7 |
|
1,99*10-3 |
|
4,00*10-2 |
20,28*10-2 |
4,98*10-3 |
27,8 |
39,6 |
|
8 |
|
2,00*10-3 |
|
4,00*10-2 |
20,32*10-2 |
4,97*10-3 |
27,0 |
38,6 |
|
9 |
|
1,99*10-3 |
|
4,01*10-2 |
20,28*10-2 |
4,97*10-3 |
27,0 |
38,2 |
|
10 |
|
1,99*10-3 |
|
4,00*10-2 |
20,26*10-2 |
4,97*10-3 |
27,4 |
38,4 |
|
|
r= 0,99*10-3 |
m= 74,19*10-3 |
R= 2,00*10-2 |
d= 20,26*10-2 |
φ= 4,98*10-3 |
To=to/30 0,91 |
T1=t1/30 1,30 |
|
|
Δl= 0,05*10-2 |
Sr= 0,001*10-3 |
Δm= 0,003*10-3 |
SR= 0,001*10-2 |
Sd= 0,02*10-2 |
Sφ= 0,01*10-3 |
ST0= 0,004 |
ST1= 0,006 |
|
Obliczenia
Obliczam odchylenia standardowe i niepewności dla poszczególnych pomiarów:
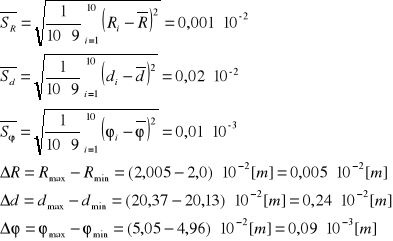
Obliczam odchylenia standardowe i niepewności związane z pomiarem dla poszczególnego drutu:
Mosiądz
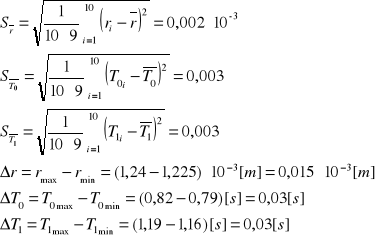
Stal
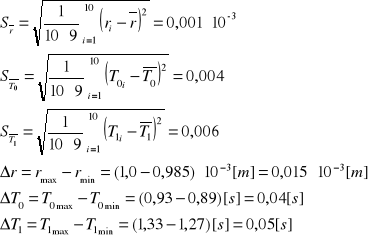
Obliczenie wartości ![]()
odległości osi krążków od osi obrotu wibratora:
![]()
Obliczenie niepewności maksymalnej pomiaru Δa:
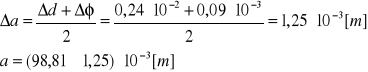
Wyznaczenie ze wzoru wartości momentu bezwładności pojedynczego krążka I1:
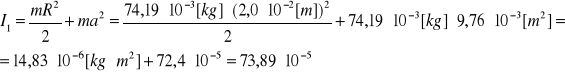
Obliczenie maksymalnej niepewności względnej tego pomiaru:
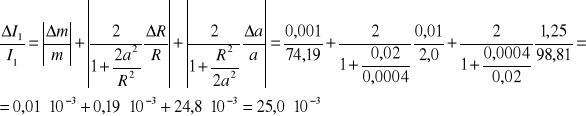
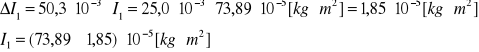
Obliczenie wartości modułu sztywności G dla drutu mosiężnego:
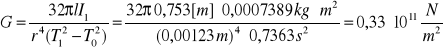
Obliczenie maksymalnej niepewności względnej tego pomiaru:

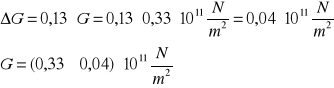
Obliczenie wartości modułu sztywności G dla drutu stalowego:
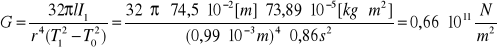
Obliczenie maksymalnej niepewności względnej tego pomiaru:
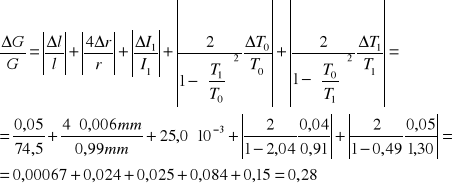
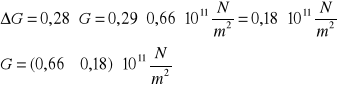
Wnioski:
|
Wartość Wyznaczona |
Wartość Tablicowa |
Mosiądz |
|
|
Stal |
|
|
Dla mosiądzu otrzymany wynik jest zgodny z wartością tablicową a dla stali jest zgodny w granicach błędu pomiarowego.
6
Wyszukiwarka
Podobne podstrony:
924 925
924
2id 924 Nieznany (2)
924
924
Część 3. Postępowanie egzekucyjne, ART 924 KPC, 2001
924
924
924
924 925
924
Seinfeld 924 The Finale(2)
924 Christina Aguilera Beautiful
924
concert 924 p
Porsche 924 technical Specif
akumulator do porsche 924 20 20 turbo
924 engine hardware v1
marche 924 1
więcej podobnych podstron