Nazwisko BŁAZIK |
WYŻSZA SZKOŁA PEDAGOGICZNA w Rzeszowie |
||||
Imię KATARZYNA |
Wykonano |
Oddano |
|||
Kierunek Fizyka z informatyką II |
13-12-2000 |
Podpis |
20-12-2000 |
Podpis |
|
Grupa laboratoryjna: XI |
|
|
|
|
|
Nr ćwiczenia
35 |
Temat ćwiczenia Wyznaczanie składowej poziomej natężenia pola magnetycznego ziemskiego przy pomocy busoli stycznych |
||||
CZĘŚĆ TEORETYCZNA
W przestrzeni otaczającej przewodnik, przez który płynie prąd elektryczny, istnieje pole magnetyczne. Natężenie i kierunek pola magnetycznego, powstałego na skutek przepływu prądu elektrycznego, zależy od długości kształtu przewodnika oraz od natężenia prądu.
![]()
(1)
Wzór ten umożliwia obliczenie pola magnetycznego w osi rdzenia cewki.
![]()
(2)
Korzystając ze wzoru (2) możemy obliczyć natężenie pola magnetycznego na zewnątrz przewodu w odległości a od osi przewodu prostoliniowego, nieskończenie długiego.
Można wyznaczyć kierunek tego pola magnetycznego i wartość jego natężenia, dzieląc w myśli przewodnik z prądem na nieskończenie małe odcinki, z których każdy jest prosty. Każdy odcinek elementarny powoduje powstanie pewnego składowego pola magnetycznego. Pole magnetyczne wytworzone przez cały przewodnik jest polem wypadkowym wszystkich pól składowych.
Kierunek natężenia pola magnetycznego wytworzonego w jakimś punkcie przestrzeni otaczającej bardzo krótki i prostoliniowy odcinek przewodnika, przez który płynie prąd jest prostopadły do płaszczyzny przechodzącej przez dany punkt przestrzeni i dany odcinek przewodnika. Jest to prawo Brota i Savarta, które obrazuje następujący rysunek:
Natężenie tego pola zgodnie z powyższym prawem wynosi:
![]()
Gdzie I oznacza natężenie prądu, dl - długość odcinka przewodnika, r - odległość między punktem S, w którym rozpatruje się natężenie pola i środkiem odcinka dl, α - kąt między odcinkiem dl i odcinkiem r.
Jeżeli przewodnik, przez który płynie prąd, ma kształt okręgu, natężenie pola magnetycznego, które powstaje w środku tego okręgu, wyznacza się następująco. Każdy odcinek dl okręgu wytwarza w środku tego okręgu pole o natężeniu:
![]()
W tym przypadku bowiem sinα=1, ponieważ kąt między każdym elementem odcinka okręgu, prostą łączącą środek tego odcinka ze środkiem okręgu jest kątem prostym.
Wartość natężenia pola wytworzonego przez poszczególne odcinki dl przewodnika są sobie równe, ponieważ odległość tych odcinków od środka okręgu jest stała (równa r). Kierunek pola wytworzonego w środku okręgu przez jakikolwiek odcinek dl jest poza tym zawsze prostopadły do płaszczyzny, w której leży okrąg (odcinek dl i środek okręgu leżą w jednej płaszczyźnie), kierunek pola wypadkowego w środku okręgu, jest więc również prostopadły do płaszczyzny okręgu. Wobec tego można dodać do siebie algebraicznie wszystkie wartości natężenia pola dH. Suma długości wszystkich odcinków dl wynosi 2πr, zaś całkowite natężenie pola w środku koła równa się:
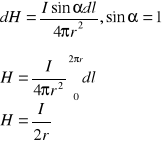
Jeżeli zamiast pojedynczego przewodnika kołowego rozpatrujemy obwód złożony z N blisko siebie położonych identycznych przewodników kołowych, które praktycznie biorąc mają poprzeczne rozmiary (grubość drutów i izolacji) znikomo małe w stosunku do promienia koła, natężenie pola w środku okręgu wynosi
![]()
gdy przez każdy przewodnik płynie prąd o natężeniu I (tzn. gdy są one połączone szeregowo, stanowiąc poszczególne zwoje wspólnego uzwojenia).
Obecność pola magnetycznego można wykazać za pomocą swobodnie zawieszonej igły magnetycznej, Która ustawia się równolegle do kierunku pola. Jeżeli rozpatrywane poprzednio uzwojenie kołowe ustawione jest pionowo i w jego środku zawieszona jest igła magnetyczna, mająca swobodę obrotu w płaszczyźnie poziomej to podczas przepływu prądu przez uzwojenie igła ta ustawia się prostopadle do płaszczyzny uzwojenia.
W tym przypadku na igłę magnetyczną działa w płaszczyźnie poziomej tylko pole magnetyczne, wytworzone przez uzwojenie kołowe. Jeżeli jednocześnie igła magnetyczna poddana zostaje działaniu jeszcze jednego poziomego pola magnetycznego, które posiada kierunek odmienny od kierunku pola magnetycznego wytworzonego przez uzwojenie, igła ustawia się wzdłuż linii sił pola wypadkowego, powstałego w miejscu, w którym się ona znajduje. Jeżeli oba wspomniane pola są prostopadłe do siebie, igła ustawia się wzdłuż przekątnej prostokąta, którego boki są wektorami tych pól. Znając natężenie pola magnetycznego H wytworzonego przez uzwojenie kołowe i kąt α, jaki tworzy igła z kierunkiem prostopadłym do tego pola (kąt π/2-α z kierunkiem pola), można wyznaczyć wartość natężenia drugiego składowego pola, oznaczymy je przez Hz z zależności
![]()
Przyrządem, który umożliwia porównanie natężenia tych dwóch pól magnetycznych jest BUSOLA STYCZNYCH albo busola tangensów (nazwa jej pochodzi od nazwy funkcji, która wyznacza stosunek H/Hz).
Pole magnetyczne ziemskie jest ukośne w stosunku do (poziomej) powierzchni Ziemi. Kąt, jaki tworzy jego kierunek z płaszczyzną poziomą, nie jest więc prosty, wartość tego kąta nazywamy inklinacją magnetyczną w danym punkcie powierzchni kuli ziemskiej.
Natomiast deklinacja magnetyczna to odchylenie igły magnetycznej od kierunku północ-południe. Wektor natężenia pola magnetycznego ziemskiego można rozłożyć na dwa wektory składowe: poziomy i pionowy.
Jeżeli płaszczyzna uzwojenia busoli stycznych leży w płaszczyźnie południka magnetycznego ziemskiego (jest to płaszczyzna pionowa, w której leży kierunek pola magnetycznego ziemskiego), kierunek pola magnetycznego wytworzonego przez prąd płynący w uzwojeniu jest prostopadły do kierunku pola magnetycznego ziemskiego. Pomiar kąta wychylenia igły α umożliwia wyznaczenie składowej poziomej natężenia pola ziemskiego.
Oznaczając przez Hz natężenie składowej poziomej, przez H - natężenie pola wytworzonego przez uzwojenie otrzymujemy:
![]()
KOLEJNOŚĆ CZYNNOŚCI DOŚWIADCZENIA:
Ustawić busolę stycznych w taki sposób, aby płaszczyzna jej uzwojenia pokrywała się z płaszczyzną południka magnetycznego Ziemi (igła magnetyczna leży wówczas w płaszczyźnie uzwojenia busoli)
2. Zestawić obwód według schematu:
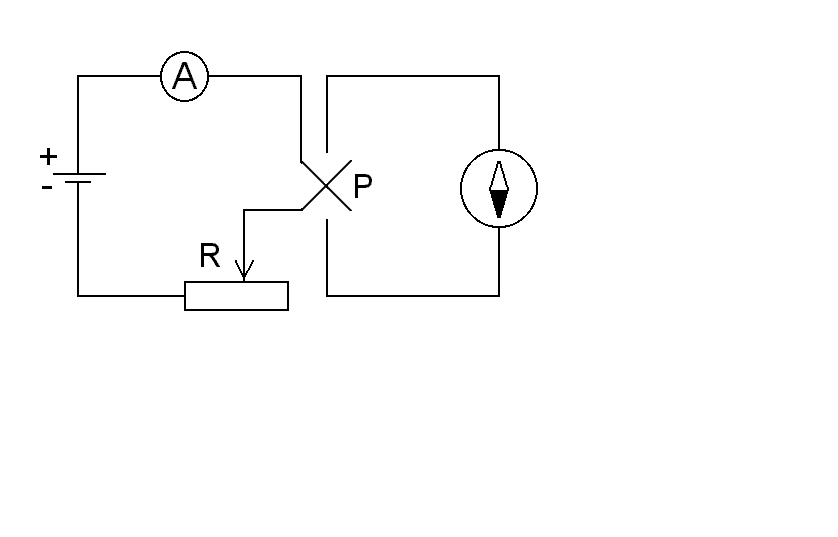
3. Zmieniając opór tak dobrać natężenie prądu, aby kąt wychylenia igły magnetycznej wynosił π/4 rad. Zanotować uzyskaną wartość natężenia. Następnie za pomocą przełącznika P zmienić kierunek przepływu prądu. Jeżeli otrzymana teraz wartość kąta wychylenia różni się o więcej niż 40 od poprzedniej, należy skorygować ustawienie busoli i rozpocząć pomiary od początku. Natomiast, jeżeli tak się nie stanie, należy kontynuować pomiary zmieniając nieco natężenie prądu, aby kąt wychylenia igły wynosił ponownie π/4 rad. Z otrzymanych w ten sposób dwóch natężeń obliczamy średnią.
Pomiary opisane w punkcie trzecim należy wykonać kolejno przy włączonych 4, 12, 24, i 40 zwojach busoli.
Na podstawie uzyskanych danych pomiarowych obliczyć wartość składowej poziomej natężenia pola magnetycznego Ziemi.
Wykonać dyskusję błędów.
Aparatura:
Busola stycznych, amperomierz, opornica suwakowa, przełącznik krzyżowy.
Ilości zwojów busoli:
Zaciski |
Ilość zwojów |
1-2 2-3 3-4 4-1 |
4 12 24 40 |
TABELKA
Obliczenia
Hpz - składowa pozioma natężenia pola magnetycznego ziemi
![]()
![]()
dla α=45o tgα=1
![]()
![]()
![]()
![]()
![]()
Błąd Hpz obliczam metodą pochodnej logarytmicznej
![]()
![]()
![]()
![]()
gdzie dla zwoju (4)
![]()
a dla zwojów (12), (24), (40)
![]()
![]()
![]()
![]()
![]()
![]()
Iśr dla (40), (24), (12), (4) to
![]()
![]()
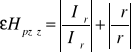
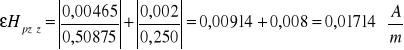
![]()
![]()
![]()
Wnioski
Po wykonaniu ćwiczenia w którym należało wyznaczyć składową poziomą natężenia pola magnetycznego Ziemi zaobserwowałam, że mierząc natężenie prądu płynącego raz w lewo, a raz w prawo, natężenie było nieco różne, co nie powinno wystąpić. Można przypuszczać, że na taki wynik wpływ może mieć stan techniczny przyrządów, które były wykorzystane w ćwiczeniu. Korzystając z natężeń uzyskanych z obliczeń wyliczyliśmy Hpz dla kolejnych liczb zwojów, a otrzymane wyniki zostały uśrednione. Błąd został policzony metodą pochodnej logarytmicznej. Składowa pozioma natężenia pola magnetycznego ziemskiego uzyskana w doświadczeniu wynosi
![]()
Wielkość podana w tablicach to około 18[a/m]. Zatem wynik uzyskany w doświadczeniu nie odbiega zbytnio od wyniku tablicowego.
1
Wyszukiwarka
Podobne podstrony:
Ćwiczenie nr 35, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwicz
Ćwiczenie nr 35, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwicz
Ćwiczenie nr 50b, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr50b
Doświadczalne spr p. Malusa, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr70
Ćwiczenie nr 82, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr82
Ćwiczenie nr 65c, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr65c
Ćwiczenie nr 65, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr65
Oscyloskop, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr85
53 wykres, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr53
Ćwiczenie nr 36, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr36
Ćwiczenie nr 8, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr8
Ćwiczenie nr 78, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr78
Siatka dyfrakc-teoria, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr67
Wnioski do Ćw 65b, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr65b
Ćwiczenie nr 6, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr6
Ćwiczenie nr 73a, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr73a
Ćwiczenie nr 42, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr42
Ćwiczenie nr 11, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr11
Ćwiczenie nr 53, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr53
więcej podobnych podstron