POLITECHNIKA WROCŁAWSKA INSTYTUT FIZYKI	SPRAWOZDANIE Z ĆWICZENIA NR 42/43 TEMAT : Pomiar rezystancji metodą techniczną i mostkową.
	DATA : OCENA :

Wstęp.

Celem przeprowadzonego ćwiczenia było :

- wyznaczanie rezystancji przez bezpośredni pomiar natężenia prądu i napięcia dla danego

rezystora metodą techniczną;

- zapoznanie z mostkową metodą pomiaru rezystancji - wykorzystanie liniowego mostka

Wheatstone'a.

1. Opis zjawiska.

METODA TECHNICZNA

W metodzie tej wykorzystywane sa dwa uklady pomiarowe:

Rys.1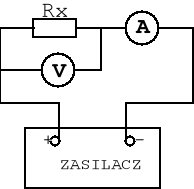
Rys.2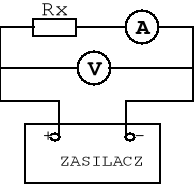

Polega ona na pomiarze napięcia panującego na końcówkach rezystora oraz prądu przepływającego przez ten rezystor. Pomiarów napięcia i natężenia dokonujemy woltomierzem i amperomierzem, rezystancję zaś obliczamy korzystając z prawa Ohma.

W układzie z rys.1 woltomierz jest włączony równolegle do mierzonego rezystora R­_x co powoduje, że napięcie mierzone na woltomierzu U_v jest takie same jak napięcie na końcówkach rezystora R_x. Wielkość mierzonej rezystancji określa zależność :

[Ω]

gdzie : R_v - rezystancja wewnętrzna woltomierza

I_v - natężenie prądu płynącego przez woltomierz [A]

U_v - napięcie zmierzone na woltomierzu

I_a - natężenie prądu zmierzone na amperomierzu

Otrzymujemy zatem :

[Ω]

Zazwyczaj w metodzie technicznej dąży się do maksymalnego uproszczenia pomiarów i obliczeń. W związku z tym można z dobrym przybliżeniem obliczać R_x ze wzoru :

co jest możliwe, kiedy natężenie prądu płynącego przez woltomierz będzie dużo mniejsze niż natężenie prądu płynącego przez R_x . Daje to nam nierówność :

R_v >> R_x.

Układ z rys.2 różni się od poprzedniego tym, że woltomierz jest włączony równolegle z mierzoną rezystancją R­_x i amperomierzem. Rezystancję R­_x określa wzór :

[Ω]

gdzie : R_a - rezystancja wewnętrzna amperomierza

U_a - napięcie na amperomierzu [V]

pozostałe oznaczenia jak wyżej.

W tym układzie stosuje się zależność R_a<<R_x , wynikającą z tego, iż spadek napięcia na amperomierzu powinien być dużo mniejszy niż spadek napięcia na R_x .

Z powyższych wzorów wynika, że układ z rys.1 będzie lepszy wówczas, gdy mierzona rezystancja R_x będzie mała. Drugi układ nadaje się do pomiaru dużych rezystancji R_x .

METODA MOSTKOWA

Rys. 3. przedstawia liniowy mostek Wheatstone'a ramiona mostka włączone są dwa rezystory R_2­ oraz badany R_x. W przekątną mostka (pkt. C) włączony jest galwanometr G. Mostek jest zasilany ze źródła Z. Wzdłuż drutu AB ślizga się kontakt K połączony z galwanometrem. Pomiar metodą mostkową polega na wykorzystaniu właściwości mostka w stanie zrównoważonym. Mostek jest zrównoważony, gdy przez galwanometr G nie płynie prąd. Wynika to z faktu, że różnica potencjałów między punktami C i O jest równa zero, czyli :

V_c=V₀

stąd

U_AC=U_AO oraz U_CB=U_OB

Ponieważ w stanie równowagi mostka przez galwanometr prąd nie płynie, więc natężenie prądu płynącego przez rezystory R_x i R₂ jest takie samo i wynosi I₁. Podobnie jest dla natężenia na drucie AB :

I₁R_x=I₂l₁ oraz I₁R₂=I₂l₂

czyli ostatecznie: [Ω]

2. Pomiary.

Oszacowanie rezystorów przy pomocy omomierza :

Rezystor	Rezystancja [Ω]
R11	500
R12	11000
R13	100
R14	650
R15	26000

Do dalszych obliczeń wybraliśmy rezystory : R12, R13, R14.

Kolejne pomiary U_V i I_a dla wybranych rezystorów przedstawia poniższa tabela :

Rezystor	U­V [V]	Ia [mA]	Rx [Ω]
	20.0	2	11538.5
R12	30.0	3	11538.5
	40.0	4	11538.5
			Rx śr = 11538.5
	0.5	7.3	68.5
R13	1	13.0	76.9
	1.5	21.0	71.4
			Rx śr = 72.3
	5.0	10.75	465.1
R14	10.0	21.0	476.2
	15.0	31.0	483.9
			Rx śr = 475.1

Oto pomiary rezystencji metodą mostkową :

Rezystor	R2 [Ω]	l1 [cm]	l2 [cm]	Rx [Ω]
	9980.0	50	50	9980
R12	14980.0	40	60	9986.7
	6770.0	60	40	10155
				Rx śr = 10040.6
	75.0	49.8	50.2	74.4
R13	111.1	40	60	74.1
	50.6	60	40	75.9
				Rx śr = 74.8
	487.0	50	50	487
R14	725.2	40	60	483.5
	330.2	60	40	495.3
				Rx śr = 488.6

3. Przykładowe obliczenia.

METODA TECHNICZNA

Wybierzmy sobie przykładowo rezystor R13 zakładając, że R_v >> R_x :

Podstawiając dane z poszczególnych pomiarów otrzymujemy :

R₁₃₍₁₎ =

R₁₃₍₂₎ =

R₁₃₍₃₎ =

Uśredniając wyniki otrzymujemy :

R_{13 śr} = 72.3 Ω

Podobnie postępujemy z R14 Dla wyliczenia R12 zakładając, że R_a<<R_x posługujemy się wzorem :

R_a = + 0.004 Ω ( Z_a - zakres miliamperomierza wyrażony w miliamperach)

Korzystając jednak z faktycznego wzoru uwzględniającego rezystancję wewnętrzną woltomierza R_V = Z*1000[Ω] ( Z - zakres woltomierza, na którym dokonaliśmy pomiarów napięcia ). W naszym przypadku Z = 75

R_V = 75*1000 = 75000 Ω

- R₁₂₍₁₎ = 11538.5 Ω

- R₁₂₍₂₎ = 11538.5 Ω

- R₁₂₍₃₎ = 11538.5 Ω

Uśredniając wyniki otrzymujemy :

R_{12 śr} = 11538.5 Ω

METODA MOSTKA LINIOWEGO:

Korzystając ze wzoru :

[Ω]

obliczam R_{13 śr}

R₁₂₍₁₎ = 9980* = 9980 Ω

R₁₂₍₂₎ = 14980* = 9986.7 Ω

R₁₂₍₃₎ = 6770* = 10155 Ω

R­_{12 śr} = 10040.6Ω

METODA MOSTKA FABRYCZNEGO:

Dla R13=100

Rx=75.95

Dla R14=650

Rx=497

Dla R12

Rx=10061

4. Rachunek błędów.

METODA TECHNICZNA

Dla układu z rys.1 :

otrzymujemy

Oznaczenia dla R13:

zakres Z_a = 30 mA błąd odczytu - 0.5%

ΔI_a = 30mA*0.5% = 0.15 mA = 0.00015 A

zakres Z_V = 1.5 V błąd odczytu - 0.5%

ΔU_v = 1.5V*0.5% = 0.04 V

R_V = 1.5*1000 = 1500 Ω

Otrzymujemy :

0.03

0.05

0.17

Dla układu z rys.2 :

otrzymujemy

Oznaczenia dla R12:

zakres Z_a = 7.5 mA błąd odczytu - 0.5%

ΔI_a = 7.5mA*0.5% = 0.0375 mA = 0.0000375 A

zakres Z_V = 75 V błąd odczytu - 0.5%

ΔU_v = 75V*0.5% = 0.375 V

R_V = 75*1000 = 75000 Ω

Otrzymujemy :

0.04

0.025

0.019

METODA MOSTKA LINIOWEGO:

R₂ = R_w

R_w - odczytana wartość rezystancji z rezystora dekadowego R_w

ΔR_W = 0.05 Ω - błąd rezystora dekadowego R_w

Δl₁ = Δl₂ =0.001 m- błąd pomiaru długości drutów l₁ i l₂

l₁,l₂ - zmierzone długości

Błąd bezwzględny przykładowo obliczamy dla R13 ( dla różnych pomiarów) :

- =

- =

- =

5. Wnioski.

Po przeprowadzonych pomiarach okazuje się, że największą dokładność daje pomiar rezystancji metodą mostkowa. Metoda techniczna dobra jest w przypadku, gdy chcemy zmierzyć opór elementu elektrycznego, a nie zależy nam na zbyt dużej dokładności. Ważne jest tu zastosowanie odpowiedniego układu elektrycznego do przeprowadzenia pomiarów. Chodzi o to, by błąd związany z potraktowaniem mierników jako idealnych (tzn. opór woltomierza równy nieskończoność, a opór amperomierza zero) był do pominięcia.

1

---