Odpowiedzi na pytania i problemy egzaminacyjne z Fizyki H1 prof.A.Radosz
I.Rozszerzający się Wszechświat
Co to oznacza „wartość krytyczna gęstości materii”?
Wartość krytyczna gęstości materii jest związana z przyszłością Wszechświata.
Są obecnie trzy wizje przyszłości
a) wszechświat się będzie rozszerzał w nieskończoność;
b) zapadnie się zpowrotem;
c) prędkość jego rozszerzania będzie malała do 0.
Który scenariusz się urzeczywistni zależy od masy Wszechświata, a masa jak wiadomo jest w prosty sposób zależna od gęstości.
Gęstość krytyczna jest to taka gęstość, dla której będzie urzeczywistniony scenariusz c). Jeżeli gęstość Wszechświata jest większa od gęstości krytycznej to będziemy mieli scenariusz b), a jeżeli mniejsza to będzie scenariusz a).
Jakie są rozmiary Galaktyki: promień i grubość dysku (wyraź w latach świetlnych)?
Przeciętną, co do rozmiaru, galaktyką jest Droga Mleczna. Jej wymiary:
- promień - 100 000 lat świetlnych (10^21 [m])
- grubość - 13 000 lat świetlnych
Ile wynosi wiek Wszechświata?
13 - 14 miliardów lat
W jakiej skali Wszechświat jest jednorodny i izotropowy?
W dużej skali, rzędu 3*108 lat świetlnych.
Omów „paradoks nocnego nieba”?
Według Newtona, Wszechświat w którym Słońce jest jedną z wielu gwiazd, powinien być nieskończony. W skończonym świecie, na skutek przyciągania grawitacyjnego nastąpiłby nieuchronnie kolaps.
Z kolei E. Halley, uzasadniał, że w nieskończonym świecie, w miarę równomiernie wypełnionym gwiazdami, oświetlenie punktu powinno być takie samo - niebo nocne powinno być jasne - wszechświat jest skończony.
Paradoks nocnego nieba wynika z tego że świat nie jest ani skończony ani nieskończony.
Wartość i sens stałej Hubble`a?
![]()
gdzie 1prs = 3,2 lat świetlnych
![]()
gdzie: V - prędość oddalania się galaktyki; r - odległość galaktyki od obserwatora.
II. Mechanika klasyczna
Przestrzeń i czas w mechnice klasycznej: jak się je traktuje w mechanice klasycznej?
Przestrzeń jest trójwymiarowa i uniwersalna. Trójwymiarowość oznacza, że potrzeba i wystarcza użyć trzech niezależnych zmiennych dla jednoznacznego określenia położenia dowolnego punktu. Uniwersalność przestrzeni polega na tym, że przedział przestrzenny jest niezmienniczy. Jeżeli zmierzymy przedmiot tym samym uniwersalnym przedmiotem to każdy mierzący otrzyma ten sam wynik.
Czas jest uniwersalny - płynie tak samo dla wszystkich obserwatorów. Obowiązuje niezmienniczość przestrzeni czasu.
Treść trzech zasad dynamiki.
I zasada: (ver.1)Jeśli na ciało nie działają siły lub działające siły się równoważą to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym. (ver.2) Istnieje inercjalny układ odniesienia.
II zasada: Jeżeli na ciało działa niezrównoważona siła zewnętrzna to ciało porusza się ruchem przyspieszonym. Przyspieszenie jest proporcjonalne do działającej siły.
![]()
III zasada: Jeśli ciało A działa na ciało B to ciało B działa na ciało A taką samą siłą lecz przeciwnie skierowaną.
Zastosowanie drugiej zasady dynamiki: przykłady równania ruchu i jego rozwiązania w następujących sytuacjach
stała
proporcjonalna do prędkości
stała siła oraz siła proporcjonalna do prędkości
oscylator harmoniczny
Oscylator harmoniczny tłumiony
Oscylator harmoniczny wymuszony
Wzdłuż jakiego toru porusza się każde z ciał w zadaniu 3)?
Ad a) torem może być prosta lub parabola;
Ad b) torem jest linia prosta.
Ad c) torem jest linia prosta.
Ad d) oscylator harmoniczny - ruch po odcinku
Ad e) jw. tłumiony - ruch po odcinku którego długość z czasem maleje
Ad f) wzmocniony - ruch po odcinku którego długość z czasem wzrasta
Wzdłuż jakiego toru porusza się ciało o masie m, jeśli działa na nie siła ciężkości skierowana wzdłuż OY? Jakie warunki początkowe należy przyjąć aby ruch odbywał się w płaszczyźnie XOY?
Jeśli działa siła wzdłuż OY, to ciało porusza się w kierunku O (ogólnie rozumiane w dół ):
A) jeśli prędkość początkowa=0 - ruch wzdłuż OY
B) jeśli prędkość początkowa różna 0, ale równoległa do OY - ruch wzdłuż OY
C) jeśli prędkość początkowa różna 0 i jej wektor nie równoległy do OY - ruch po paraboli
Ciało porusza się w płaszczyźnie XOY jeśli wektor prędkości początkowej leży w tej płaszczyźnie.
Ruch po okręgu:
Opis we współrzędnych biegunowych
Niech promień okręgu wynosi r. Położenie punktu na okręgu można jednoznacznie określić podając kąt φ zakreślony przez promień wodzący. Ruch ciała jest określony przez funkcję φ= φ(t). Jeżeli przez s oznaczymy drogę przebyta przez ciało po okręgu w czasie, w którym droga kątowa wynosiła φ, to zachodzi związek: s = φr.
Prędkość i przyspieszenie
Różniczkujemy równanie s = φr względem czasu
![]()
=> v = ωr
gdzie: v - prędkość linowa, ω- prędkość kątowa
Różniczkujemy równanie v = ωr względem czasu
![]()
=> as = εr
gdzie: as - przyśpieszenie styczne, ε - przyspieszenie kątowe,
Przyśpieszenie normalne w ruchu po okręgu nazywamy przyśpieszeniem dośrodkowym ( skierowane do srodka). Wynosi ono: ![]()
Prędkość i przyśpieszenie kątowe są wielkościami wektorowymi, których kierunki są równoległe do siebie i prostopadłe do płaszczyzny okręgu. Zwrot wektora ![]()
jest wyznaczany zgodnie z regułą śruby prawoskrętnej - zwrot wektora ![]()
pokrywa się z kierunkiem ruchu postępowego śruby prawoskrętnej, która obraca się zgodnie z kierunkiem ruchu punktu po okręgu. Wektor przyśpieszenia kątowego ![]()
ma zwrot zgodny z wektorem![]()
w przypadku przyspieszonego ruchu po okręgu (ε >0) i przeciwny w przypadku ruchu opóźnionego (ε<0).
Jednostajny i zmienny ruch po okręgu
Ruch jednostajny:
Jest to ruch którego prędkość kątowa ω = const, a droga kątowa jest liniową funkcją czasu.
Droga kątowa przebyta przez punkt: φ = φ0 + ωt gdzie: φ0 - kąt początkowy, ω - prędkość kątowa (ω = const), t - czas ruchu.
Dla φ0 = 0 zależność prędkości kątowej i drogi kątowej od czasu przedstawiają rysunki poniżej:
Ruch jednostajny po okręgu można scharakteryzować okresem T, czyli czasem potrzebnym na przebycie długości obwodu okręgu ( co odpowiada drodze kątowej 2π): ![]()
. Liczbę pełnych obiegów w jednostce czasu wynosi ![]()
Ruch jednostajnie zmienny:
Jest to ruch ze stałym przyśpieszeniem kątowym ε. Prędkość kątowa ω jest liniową funkcją czasu t.
Prędkość kątowa: ω = ω0 + εt gdzie: ω0 - prędkość kątowa początkową; ε - przyśpieszenie kątowe (ε = const).
Droga kątowa przebyta przez punkt: φ = φ0 + ω0t+½ εt2 gdzie: φ0 - kąt początkowy, ω0 - prędkość kątowa początkowa, ε - przyspieszenie kątowe.
Jeśli ε > 0 to mamy ruch jednostajnie przyśpieszony, jeśli ε < 0 - ruch jednostajnie opóźniony.
Zależność ω = ω(t) w przypadku, gdy ε > 0 przestawiono na wykresie:
Omów zjawisko rezonansu?
Rezonans jest to zjawisko występujące dla rzeczywistych oscylatorów tłumionych przy pewnej charakterystycznej wartości częstości wymuszającej ωr, kiedy amplituda oscylacji osiąga maksiumu. Częstość ωr, przy której pojawia się maksymalna amplituda drgań wymuszonych danego układu, nazywamy częstością rezonansową. Im mniejsze tłumienie układu, tym częstość rezonansowa bliższa jest częstości ωo układu nietłumionego.
gdzie:
F0 - amplituda siły wymuszającej;
ωo - częstość drgań własnych
β - współczynnik tłumienia
![]()
r - współczynnik oporu ośrodka;
k - współczynnik proporcjonalności między siłą a wychyleniem;
Omów kwestie zachowania: pędu, energii, momentu pędu.
Zasada zachowania pędu: Całkowity pęd układu izolowanego, tzn. takiego, który nie oddziałuje, z otoczeniem, jest zachowany.
Dla cząstki swobodnej: ![]()
Dla układu dwóch cząstek pęd jest suma pędów poszczególnych cząstek:
![]()
Zasada ta obowiązuje w mechanice klasycznej i relatywistycznej.
Zasada zachowania energii: Suma energii kinetycznej i potencjalnej jest stała.
Ep + Ek= Ec = const.
Zasada ta obowiązuje w mechanice klasycznej i relatywistycznej.
Zasada zachowania momentu pędu: Jeżeli układ jest izolowany, moment pędu jest zachowany.
![]()
W przypadku jakich sił zachowana jest energia mechaniczna?
Energia mechaniczna jest zachowana w przypadki pola sił zachowawczych. Pole sił jest polem zachowawczym, jeśli praca potrzeba na przesunięcie ciała z dowolnego punktu A do dowolnego punktu B nie zależy od drogi, po jakiej ciało będzie przesuwane.
Dla wymienionych niżej sił określ energię potencjalną:
![]()
Jest to siła w ruchu harmonicznym.
Jest to siła w polu grawitacyjnym.
Jest to siła oporu ośrodka.
EP nie istnieje, ponieważ siła oporu nie jest siłą zachowawczą.
Jest to siła w polu sił centralnych.
Zagadnienie ruchu w polu siły centralnej
Zachowane wielkości
Zachowane wielkości to stała energia układu i stały moment pędu.
Dlaczego Ziemia porusza się po orbicie, która leży w płaszczyźnie?
1.Ponieważ moment pędu w polu siły centralnej jest zachowany: ![]()
2.Energia układu w polu siły centralnej jest zachowana: ![]()
Dlaczego planety w Układzie Słonecznym poruszają się w tej samej płaszczyźnie?
Powód wiążę się z historią powstania Układu Słonecznego.
Mianowicie układ słoneczny powstał z chmury materii, która się bardzo wolno obracała. Na skutek kurczenia się tego obłoku (zapadania do środka pod wpływałem grawitacji) prędkość obrotów zaczęła rosnąć. Materia, która znajdowała się w płaszczyźnie prostopadłej do osi obrotów poruszała się najszybciej, aż wreszcie jej prędkość była na tyle duża, że siła odśrodkowa, jaka na nią działa zrównała silę przyciągania grawitacyjnego środka i tak powstały planety. Pozostała materia obracała się zbyt wolno, więc została wciągnięta przez powstające Słońce.
Zagadnienie „prędkości ucieczki”: sens, wartości; kiedy pole grawitacyjne jest silne?
Druga prędkość kosmiczna tzw. prędkość ucieczki jest to najmniejsza prędkość z jaką należy wystrzelić rakietę na powierzchni Ziemi, aby uciekła ona z pola grawitacyjnego Ziemi.
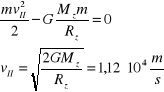
Energia całkowita tej rakiety poza polem grawitacji Ziemi ma wynosić zero. Energia całkowita jest zachowana, a więc musi się zerować i na powierzchni Ziemi.
Pole grawitacyjne jest silne wtedy, gdy prędkość ucieczki jest porównywalna do prędkości światła.
Omów zagadnienie sił bezwładności. Dlaczego siły bezwładności nazywa się „siłami pozornymi”?
Siły bezwładności występują w nieinercjalnym układzie odniesienia (układ w którym żyjemy) i są przeciwnie skierowane do przyśpieszenia. Nazwa sił pozornych pochodzi stąd, że obserwator nieruchomy (inercjalny) ich nie dostrzega. Widzi je tylko obserwator nieinercjalny, ale i on nie jest w stanie znaleźć ciał, od których siły te mogłyby pochodzić.
Kamień spada z wieży znajdującej się na półkuli północnej. W jakim kierunku odchyli się pod wpływem siły Coriolisa ? Jak dalece?
Odchyli się w kierunku wschodnim.
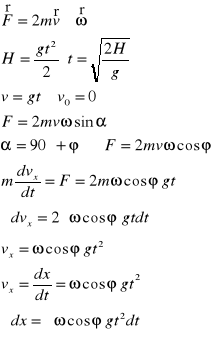
![]()
- odchylenie pod wypływem siły Coriolisa
Rzeka płynie z południa na północ na półkuli północnej. Który z jej brzegów powinien być podmywany na skutek działania siły Coriolisa?
Podmywany jest brzeg wschodni, ponieważ siła Coriolisa ma taki kierunek.
Zapisz wyrażenia dla sił bezwładności: odśrodkowej, unoszenia i Coriolisa?
Siła bezwładności w ruchu postępowym:
Siła odśrodkowa bezwładności jest to siła, która pojawia się w wirującym, względem pewnego układu inercjalnego, układzie odniesienia. Taka siła działa na ciało w tym układzie niezależnie od tego czy ciało spoczywa w tym układzie czy porusza się względem niego.
![]()
Siła bezwładności Coriolisa pojawia się jeśli ciało porusza się względem wirującego układu odniesienia. Jest ona skierowana prostopadle do wektora prędkości ciała ![]()
i wektora prędkości kątowej ![]()
obracającego się układu. Znika gdy ciało w układzie wirującym spoczywa tzn. gdy ![]()
=0 oraz gdy ciało porusza się równolegle do osi obrotu układu tzn. gdy ![]()
||![]()
.
Druga zasada dynamiki Newtona w układzie nieinercjalnym: ![]()
Wymień postulaty szczególnej teorii względności?
1.Prawa przyrody są takie same w inercjalnych układach odniesienia.
2.Prędkość światła jest taka sama (niezmiennicza) dla wszystkich inercjalnych obserwatorów (światło rozchodzi się w układzie inercjalnym z prędkością jednostajną c = 3·108 m/s).
Skąd wynika, że prędkość światła jest niezmiennicza?
ver.1 Dlatego, że mion dociera do ziemi, mimo że nie powinien według teorii "klasycznej".
ver.2 Prędkość światła jest taka sama dla wszystkich inercjalnych obserwatorów.
Zapisz transformacje Galileusza.
x = x` + d = x` · ut
y = y`
z = z`
t = t`
gdzie: d - położenie początku układu X`Y`Z` w układzie XYZ, u - prędkość układu X`Y`Z` względem układu XYZ.
Zapisz transformacje Lorentza.
[na rys. v0 to u]
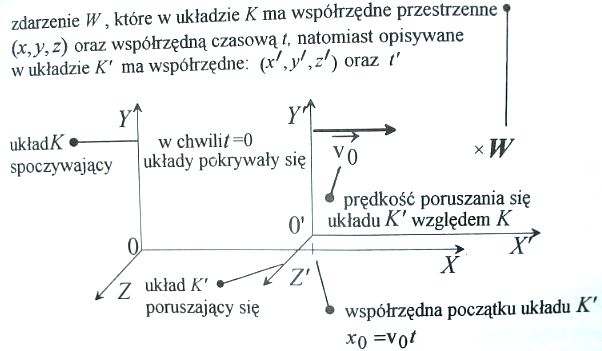
Współrzędne przestrzenne zdarzenia (x,y,z) i współrzędna czasowa t zdarzenia dla obserwatora związanego z układem K (po lewej).
Współrzędne przestrzenne zdarzenia (x`,y`,z`) i współrzędna czasowa t` zdarzenia dla obserwatora związanego z układem K`. (po prawej)
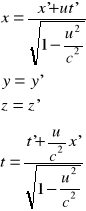
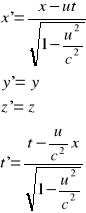
Co to znaczy „skrócenie długości”?
Skrócenie długości jest jedną z konsekwencji transformacji Lorentza. Wzór na skrócenie Lorentza wynika z transformacji Lorentza przy założeniu, że pomiar położenia początku i końca pręta w układzie XYZ, w którym pręt się porusza, został dokonany w tej samej chwili czasu.
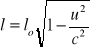
gdzie: l - długość pręta mierzona w układzie XYZ (l = x2 - x1); lo - długość pręta mierzona w układzie X`Y`Z` (lo = x`2 - x`1); u - prędkość względna obu układów; c - prędkość światła.
Co to znaczy „dylatacja czasu”?
Dylatacja czasu jest jedną z konsekwencji transformacji Lorentza. Wzór na dylatację czasu wynika z transformacji Lorentza przy założeniu że położenie cząstki w układzie X`Y`Z` dla chwili t`2 i t`1 jest takie samo.
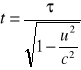
gdzie: t - czas między dwoma zdarzeniami mierzony w układzie XYZ (t = t2 - t1); τ - czas własny - czas miedzy dwoma zdarzeniami, które zaszły w tym samym miejscu układu X`Y`Z`, mierzony w układzie X`Y`Z` (τ = τ 2 - τ 1)
Wyprowadź oba te zjawiska na przykładzie muonu, którego czas życia wynosi 2.2 mikrosekundy, a przebywa on drogę 15 krotnie dłuższą niż powinien!
a) skrócenie długości
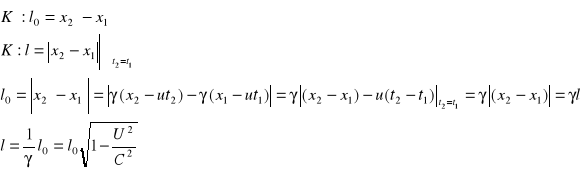
b) dylatacja czasu
![]()
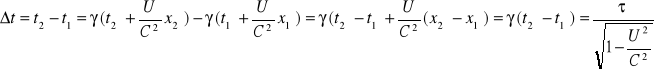
Dlaczego czas i przestrzeń nie są uniwersalne?
Niezmiennicza prędkość światła oznacza, że wektorowe składanie prędkości ma ograniczony charakter (nie obowiązuje dla prędkości światła). Oznacza to, że również transformacje Galileusza nie są uniwersalne i co za ty idzie, nie są spełnione założenia o niezmiennym charakterze przedziału przestrzennego i czasowego, a więc czas i przestrzeń nie jest uniwersalna.

Jakie wielkości są uniwersalne?
Wielkości uniwersalne są takie same dla wszystkich inercjalnych obserwatorów. Są nimi:
prędkość światła w próżni c = 3·108 m/s
interwał czasoprzestrzenny:
Co to znaczy równoważność masy i energii?
Równoważność masy i energii jest jednym z wniosków szczególnej teorii względności.
Zachowanie całkowitej energii jest równoważne zachowaniu masy relatywistycznej: E=mc2. Relacja ta wyraża fakt, że energia i związana z nią masa mogą być mierzone w jednostkach energii lub równoważnie w jednostkach masy.
Zapisz wektor relatywisycznego pędu.
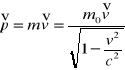
gdzie: mo - masa spoczynkowa cząstki
Zapisz zerową składową czterowektora pędu.
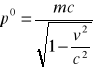
Odpowiedzi zostały opracowane dzięki współpracy użytkowników forum: www.air.ict.pwr.wroc.pl/forum.php
Podziękowania należą się dla user'ów: sojer, atris, smukwij, kasiunia, Eli, Kuzio, bobby, Did, aman.
Wniosek jest jeden: oby więcej takich inicjatyw !!
Odpowiedzi do zagadnień na egz. Fizyka H1 prof. A.Radosz
9
Wyszukiwarka
Podobne podstrony:
Bilans 20.02.2008, POLITECHNIKA, AiR, Semestr II, FIZYKA, Fizyka dla elektroników
Oscylator harmoniczny, POLITECHNIKA, AiR, Semestr II, FIZYKA, WYKŁADY
L.1 Wektory kinem dynamika, POLITECHNIKA, AiR, Semestr II, FIZYKA, Fizyka dla elektroników
L.3 Ruch obrotowy, POLITECHNIKA, AiR, Semestr II, FIZYKA, Fizyka dla elektroników
Pytania 2008, POLITECHNIKA, AiR, Semestr II, FIZYKA, Fizyka dla elektroników
33, POLITECHNIKA, AiR, Semestr II, FIZYKA, Fizyka dla elektroników
Odp Na Pytania 2008 ver 1.0, POLITECHNIKA, AiR, Semestr II, FIZYKA, Fizyka dla elektroników
0profradoszodp2006, POLITECHNIKA, AiR, Semestr II, FIZYKA, Fizyka dla elektroników
sprawko(1), POLITECHNIKA, AiR, Semestr II, FIZYKA POLPRZEWODN IKOWA, LABORATO RIUM, 01
Odp Na Pytania 2008 ver 1.5, POLITECHNIKA, AiR, Semestr II, FIZYKA, Fizyka dla elektroników
Odp Na Pytania 2008 ver 1.1, POLITECHNIKA, AiR, Semestr II, FIZYKA, Fizyka dla elektroników
Bilans 20.02.2008, POLITECHNIKA, AiR, Semestr II, FIZYKA, Fizyka dla elektroników
Przyklad Test, PWR, Automatyka i Robotyka (AIR), Semestr II, Fizyka 3.3, Wykład
fizyka egzamin, AiR, SEMESTR II, Fizyka II
notatka, POLITECHNIKA, AiR, Semestr II, AUTOMATYKA I ROBOTYKA, 06
automatyka i robotyka-rozwiazania, POLITECHNIKA, AiR, Semestr II, AUTOMATYKA I ROBOTYKA, KOLOKWIUM
więcej podobnych podstron