Numer ćwiczenia: 1	Temat ćwiczenia: Drgania harmoniczne sprężyny	Ocena z teorii:
Nr zespołu: 9	Imię nazwisko: Mariusz Sypek	Ocena z zaliczenia ćwiczenia:
Data: 19.04.2007	Wydział: Rok: Grupa: EAIE 1b 7	Uwagi:

Cel ćwiczenia

Wyznaczenie współczynnika sprężystości sprężyny i modułu sztywności materiału sprężyny, sprawdzenie zgodności teorii opisującej wahadło sprężynowe z doświadczeniem.

Wprowadzenie

Drgania, oscylacje, procesy fizyczne opisywane funkcjami na przemian rosnącymi i malejącymi. Drgania klasyfikuje się na podstawie matematycznych własności funkcji opisujących je. Wyróżnia się drgania probabilistyczne (jeśli przyszły stan nie daje się jednoznacznie ściśle określić) i deterministyczne. Te ostatnie dzielą się na okresowe i nieokresowe (inaczej: periodyczne i nieperiodyczne).

Okresem drgań nazywamy czas potrzebny do wykonania jednego cyklu drgań. Jeśli amplituda maleje w czasie, drgania nazywamy gasnącymi (tłumionymi). Drgania można też dzielić na swobodne i wymuszone (wywołane zewnętrzną, zmienną w czasie, siłą). Drgania deterministyczne opisywane są równaniami różniczkowymi.

Drgania harmoniczne

Szczególnym rodzajem drgań są drgania harmoniczne, tj. okresowe, o stałej amplitudzie, opisane sinusoidą. Ze względu na prostotę opisu drgania harmoniczne są wykorzystywane do opisu wielu drgań rzeczywistych jako ich przybliżenie (lub poprzez rozkład na nie).

Najprostsze równanie opisujące drgania harmoniczne (dla ciężarka zawieszonego na sprężynie) ma postać:

mx'' (t) + kx(t) = 0.

Rozwiązaniem jest funkcja

x(t) = A·sin(ωt+ϕ₀),

gdzie A - amplituda drgań, ω = 2πν = (k/m)^0.5, ω - częstość kołowa (ν - częstość drgań), k - współczynnik sprężystości, m - masa ciała, ϕ₀ - faza początkowa. Ze względu na fizykę procesów wyróżnia się drgania mechaniczne i elektryczne.

Wyrażenia na prędkość liniową v oraz na przyspieszenie a w ruchu harmonicznym:

v = dx/dt = Aωcos(ωt + ϕ₀),

a = dv/dt = d²x/dt² = - Aω²sin(ωt + ϕ₀),

Znając wyrażenie na przyśpieszenie a możemy zapisać wzór na siłę F, która musi działać na ciało, żeby poruszało się ono ruchem harmonicznym (np. sinusoidalnym). Zgodnie z zasadami dynamiki Newtona otrzymujemy:

,

F = -kx,

gdzie k jest stałą sprężystości zdefiniowaną:

k = mω².

Stąd relacja:

ω = (k/m)^1/2.

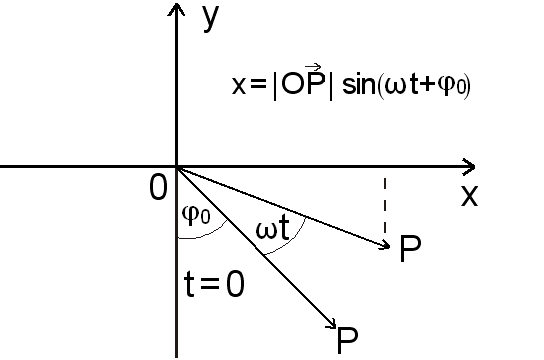
Wychylenie ciała w ruchu harmonicznym można zilustrować za pomocą wektora wirującego.

Wychylenie ciała w ruchu sinusoidalnym można rozważyć, jako składową x-ową wektora OP, którego moduł |OP| = A. Wektor OP obraca się przeciwnie do ruchu wskazówek zegara wokół osi O, z prędkością kątową ω i dla t = 0, tworzy kąt ϕ₀ z osią y.

Energia kinetyczna E_k

Korzystamy z definicji energii kinetycznej, wykorzystujemy związek:

v = dx/dt = Aωcos(ωt + ϕ₀),

E_k = ¹/₂ mv² = ¹/₂ m[ω²A²cos²(ωt + ϕ₀)]

lub po przekształceniu:

E_k = ¹/₂ mω ²[A² - A²sin² (ωt + ϕ₀)]

E_k = ¹/₂ mω ² (A² - x²)

Energia potencjalna E_p

Korzystamy z definicji opisanej wzorem
, rozważamy przypadek jednowymiarowy:

F = - dE_p/dx

kx = dE_p/dx

Po scałkowaniu otrzymujemy:

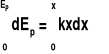
E_p = ¹/₂ kx² = ¹/₂ kA²sin²(ωt + ϕ₀)

Po przekształceniu, wykorzystując związek k = mω² otrzymujemy:

E_p = ¹/₂ mω²A²sin²(ωt + ϕ₀) = ¹/₂ mω²x²

Dla x = A energia potencjalna przyjmuje wartość maksymalną:

E_p = ¹/₂ mω²A²

Energia całkowita E

E = E_k + E_p

E = ¹/₂ mω²(A² - x²) + ¹/₂ mω²x²

E = ¹/₂ mω²A²

Stała k jest zależna od charakteru sił, pod wpływem których porusza się drgająca masa. Np. dla wahadła matematycznego o długości l siła powodująca powrót układu do położenia równowagi jest siłą ciężkości i wtedy k = mg/l. Gdy o ruchu decyduje sprężystość ciała (np. drgania sprężyny, drgania pręta), stała k związana jest właśnie z własnościami sprężystymi materiału, tj. modułem Younga E lub z modułem sztywności G, oraz zależy od wymiarów geometrycznych układu. W przypadku sprężyny teoria sprężystości pozwala obliczyć stałą k na podstawie modułu sztywności G materiału oraz wymiarów geometrycznych: promienia zwoju sprężyny R, promienia r drutu, z którego wykonano sprężynę i liczby zwojów sprężyny n.

.

Przy wyprowadzaniu wzorów dla drgań harmonicznych przyjęliśmy dwa założenia upraszczające. Po pierwsze, nie uwzględniliśmy sił grawitacji. Po drugie nie uwzględniliśmy masy sprężyny, która, obok masy ciężarka, też uczestniczy w drganiach. Obecnie rozpatrzymy kolejno wpływ obydwu czynników.

W przypadku nieważkiej sprężyny, na której zawieszono masę M oprócz siły sprężystości działa jeszcze stała ciężkości, tak że całkowita siła wynosi:

F = -kx + Mg.

W powiązaniu z II zasadą dynamiki daje to równanie ruch w postaci:

Ma = -kx + Mg.

Ponieważ a = d²x/dt², otrzymujemy równanie różniczkowe:

.

Rozwiązanie tego równania różniczkowego na nieznaną funkcję x(t) ma postać:

,

gdzie
oraz
.

Z porównania z równaniem x(t) = A·sin(ωt+ϕ₀) widać, że jest to ruch harmoniczny, lecz zachodzący względem położenia x₀, jakie przybierze masa M statycznie zawieszona na sprężynie.

W przypadku realnej sprężyny, której masy m nie można zaniedbać wobec masy obciążnika M odpowiednie wyrażenie na T ma postać:

.

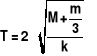
Tę zależność można otrzymać porównując energię kinetyczną ciężarka M równą
i energię kinetyczną sprężyny m, której koniec ruchomy porusza się z tą samą prędkością v, natomiast punkt zaczepienia spoczywa. Rozpatrzmy element sprężyny o długości dx o masie równej dm = m (dx/l₀). Jego prędkość wynosi v(x) = v (x/l₀). Zatem energia kinetyczna elementu sprężyny dm wynosi:

.

Całkowita energia kinetyczna sprężyny wynosi:

.

Całkowita energia kinetyczna układu ciężarka i sprężyny wynosi:

.

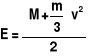
Sprężyste odkształcenie, odwracalne odkształcenie ciała. W przypadku idealnym po zaprzestaniu działania sił wywołujących sprężyste odkształcenie ciała powraca ono samoczynnie do swego pierwotnego kształtu.

W przypadku ciał rzeczywistych sprężyste odkształcenie zachodzi tylko w przybliżeniu ze względu na istnienie zjawiska histerezy (sprężystej).

Prawo Hooke'a, prawo określające zależność między siłą odkształcającą a odkształceniem dla ciała sprężystego (w granicy sprężystości).

Dla pręta o długości l ściskanego (rozciąganego) siłą F działającą równolegle do osi długiej pręta, prawo Hooke'a wyraża się wzorem: Δl = Fl/sE, gdzie: Δl - wydłużenie, s - pole przekroju poprzecznego pręta, E - moduł Younga (moduł sprężystości). W ogólności prawo Hooke'a ma postać prawa tensorowego, o 21 stałych elastycznych.

Moduł Younga, podłużny moduł sprężystości, współczynnik sprężystości wzdłużnej, E, wielkość charakteryzująca sprężystość danego ciała.

E = σ/ε,

gdzie: σ - naprężenie normalne, ε - względne wydłużenie ciała. Odwrotność modułu Younga α = 1/E nazywana jest współczynnikiem wydłużenia.

Modułem sztywności G nazywamy stosunek naprężenia stycznego  do wywołanego przez nie odkształcenia postaci γ.

W celu wyznaczenia G wykorzystujemy zjawisko skręcenia pręta, gdyż podatność materiału na skręcenie zależy wyłącznie od modułu sztywności G i rozmiarów geometrycznych pręta.

---