WILiŚ Gdańsk 10.05.2013r.

Budownictwo sem. 3

Grupa 8 A

Marek Łukianiuk

Bartosz Krusiński

Marta Łupina

Sprawdzał:

dr inż. Michał Hirsz

Sprawozdanie z ćwiczeń laboratoryjnych

Ćwiczenie 12: Wyznaczenie reakcji podporowej belki ciągłej

1.Doświadczenie 1 - Wyznaczanie wartości reakcji podporowej.

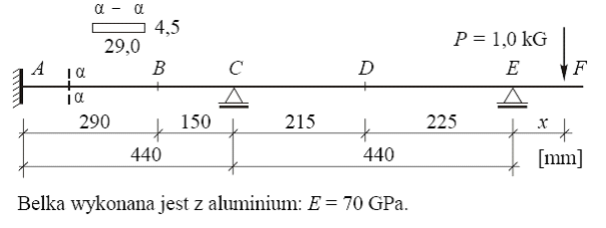
Celem doświadczenia pierwszego było wyznaczenie wartości reakcji podporowej belki ciągłej w podporze C. Obciążyliśmy belkę wg. rys siłą P=9.8N w odległości 0.20 m na prawo od podpory E. Następnie odczytaliśmy wskazanie czujnika w punkcie C , co dało nam odczyt początkowy. Wówczas zdjęliśmy obciążenie I odrzuciliśmy podporę C. Po powtórnym obciążeniu belki (rys.1 - bez podpory C). Odczytaliśmy powtórnie wskazanie czujnika w punkcie C (odczyt końcowy). Następnie w miejscu podpory C umieściliśmy szalkę i przez dosypywanie śrutu sprowadziliśmy punkt C do położenia pierwotnego wyznaczonego odczytem początkowym. Ciężar zawieszony w punkcie C zważyliśmy (tzn. masę śrutu w szalce).

2. Doświadczenie 2 - Wyznaczenie przemieszczeń punktów B i D belki ciągłej.

Na nieobciążonej belce odczytaliśmy wskazania czujników w punktach B i D (odczyty początkowe). Następnie obciążyliśmy belkę siłą P=9.8 N w odległości 0.23m na prawo od podpory E i ponownie odczytaliśmy wskazania czujników w punktach B i D (odczyt końcowy).

3. Wyniki pomiarów

3.1. Doświadczenie 1.

x = 20 cm = 0.2 m

Punkt	C [mm]
OP	1,52
OK	4,39
d [mm]	-2,87

ciężar szalki ze śrutem: m = 924 g * 9.81 = 9,064 N = R_c

3.2. Doświadczenie 2.

x = 23cm = 0.23 m

punkt	B	D
OP	3,17	2,79
OK	2,89	4,14
d [mm]	-0,28	-1,35

4. Obliczenia teoretyczne.

1. Obliczenie reakcji w punkcie C.

δ₁₀ + δ₁₁X₁ + δ₁₂ X₂ = 0

δ₂₀ + δ₂₁X₁ + δ₂₂ X₂ = 0

δ₁₀ =
(0 + 0 + 0) = 0

δ₂₀ = -
(44 *
* 1 * 245) = -

δ₁₁ =
(44 *
* 1 * 1) =

δ₂₂ =
(2*44 *
* 1 * 1) =

δ₂₁ = δ₁₂=
(44 *
* 1 * 1) =

2 1 X₁ 0

=

1 4 X₂ 245

Po przeliczeniu macierzy otrzymujemy wyniki:

X₁ = -35 Ncm

X₂ = 70 Ncm

Wyznaczenie reakcji podporowej R_C: R_C = Rc₀ + X₁*R_C1 + X₂*R_C2 = 9,55 N

4.2 Obliczenie przemieszczeń punktów B, C, D.

δ_ = 1/EJ (0.5*0.88*0.88*2/3*0.88) = 0.227 / EJ

δ_ = 1/EJ (-0.5*0.88*0.88 ( 1/3*2.26 + 2/3*10.89)) = -3.10 / EJ

x₁ = 13.656 N

EJ = 70 E9 * 2.2022 E-10 = 15.415 Nm⁴

4.2.1 Przemieszczenie punktu C.

δ_C = 1/EJ (-0.5*0.44*0.44 [1/3*(1.139+0.473) - 0.473] = -0.00040 m

4.2.2 Przemieszczenia punktów B i D.

δ_B = 1/EJ (-0.5*0.29*0.29 (2/3*0.28 - 1/3*0.27) = 0.00026 m

δ_D = 1/EJ (-0.5*0.655*0.44 (-2/3*0.28 + 1/3*0.56) - 0.5*0.215*0.44 (2/3*0.56 - 1/3*0.28) - 0.5*0.215*0.215 (2/3*0.56 - 1/3*0.816)) = -0.001 m.

5. Wnioski.

wyniki	doświadczalne	teoretyczne
RC [N]	9,06	9,55
dB [mm]	0,28	0,26
dD [mm]	-1,35	-1

Wyniki pomiarów doświadczalnych i obliczeń teoretycznych różnią się. Błędy pomiarowe wynoszą odpowiednio: R_C = 5,41%, δ_B = 7,28%, δ_D = 35.00%. Błąd ten można uznać za dopuszczalny, jeśli przyjąć, że operujemy małymi wartościami których pomiar wymaga dużej precyzji i zachowania szczególnej ostrożności przy wykonywaniu pomiarów, gdyż nawet niewielkie wstrząsy badanego układu powodują jego znaczne przemieszczenia co prowadzi do przekłamania wyników. Częściowy wpływ na otrzymane wyniki ma także dokładność przyrządów pomiarowych co ma szczególne znaczenie przy pomiarze małych wielkości. Również obliczenia teoretyczne oparte są na wzorach uproszczonych, a otrzymane wyniki charakteryzują się pewną tolerancją dokładności. Wszystkie przedstawione powyżej czynniki mają wpływ na wartości otrzymanych błędów określających różnice między wynikami pomiarów i obliczeń.

---