Magnetostatyka
Prawo Biota-Savarta
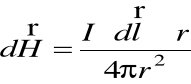
co po scałkowaniu daje całkę przestrzenną:
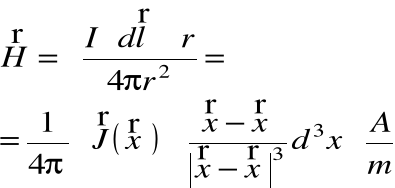
Po poniższych przekształceniach można pokazać:
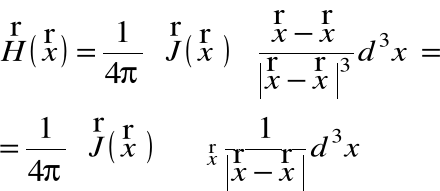
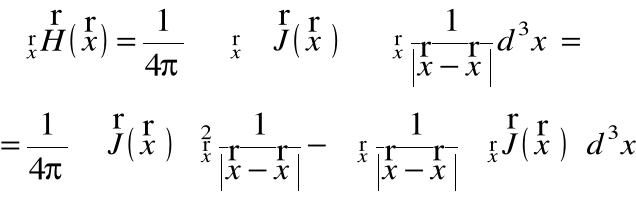
Korzystając z prostego twierdzenia:
![]()
Czyli otrzymujemy?
![]()
Siła oddziaływująca na przewodnik z prądem:
![]()
dla pojedynczego ładunku - siła Lorenza
![]()
lub w wersji continuum
![]()
Związki materiałowe:
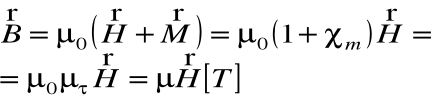
diamagnetyki ![]()
<0
paramagnetyki ![]()
>0
ferromagnetyki ![]()
>>0 około 103
ferrimagnetyki ![]()
>>0 około 105 (Fe18Ni75Cu5Cr2)
rotacja z pola magnetycznego
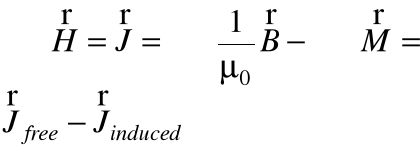
Co oznacza, że efektywny prąd w materiałach może być przedstawiony jako suma prądów swobodnych i indukowanych. Przy czym prądy indukowane należy rozumieć w sensie prądów odpowiedzialnych za momenty magnetyczne zdefiniowanych jako:
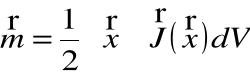
dla prostego przypadku prądu kołowego o promieniu r i natężeniu I powyższy wzór przyjmuje postać:
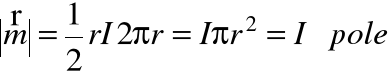
jednocześnie moment magnetyczny związany z indukowanym prądem jest równy:
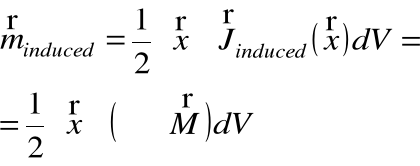
składowa i tego momentu jest równa:
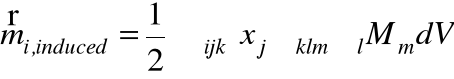
a ponieważ
![]()
składowa i momenty magnetycznego może być zapisana jako
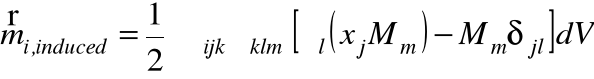
Magnetyzacja zanika jednak szybciej niż 1/x więc pierwsza część w nawiasach kwadratowych znika pozostaje więc:
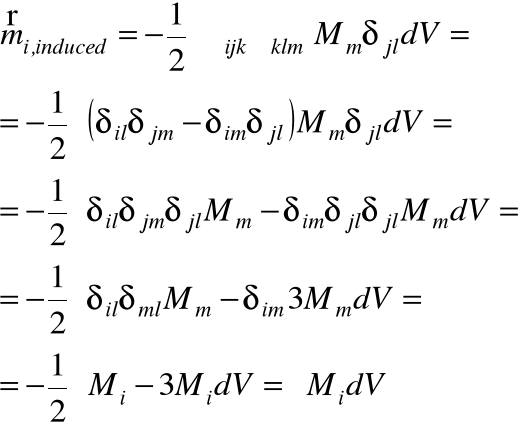
Czyli dla całego momentu magnetycznego otrzymujemy:
![]()
![]()
magnetyzacja jest więc gęstością momentu magnetycznego.
Ważny wniosek; moment magnetyczny materiału jest zależny od namagnesowania i objętości a nie zależy od kształtu.
(Nie ma czegoś takiego jak monopol magnetyczny - odpowiednik ładunku elektrycznego chociaż można wprowadzić matematycznie taką wielkość.)
Dla pola magnetycznego można wprowadzić pojęcie potencjału. Będzie to jednak w przeciwieństwie do pola elektrycznego potencjał wektorowy, który oznaczmy przez ![]()
![]()
Potencjał ten zależy od przepływających prądów:
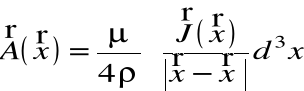
Pola złożone
Teoria pól złożonych pozwala w systematyczny sposób przybliżać pola pochodzące od złożonych rozkładów ładunków czy prądów.
Rozłóżmy odwrotność odległości na szereg:
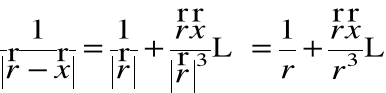
gdzie ![]()
oznacza położenie punktu, w którym określamy pole natomiast ![]()
określa położenie źródła pola.
Stosując ten szereg do potencjału otrzymamy:
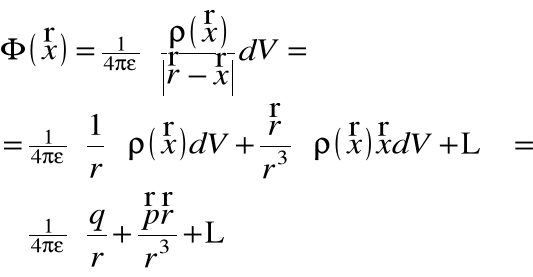
Pierwsza część monopolowa pochodzi od ładunku q, druga dipolowa od momentu dipolowego p, następna trzecia kwadrupolowa...
Licząc gradient z potencjału otrzymujemy wektor pola elektrycznego:
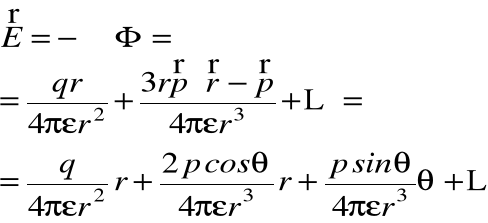
Co za tym idzie energia związana z rozkładem ładunków wynosi:
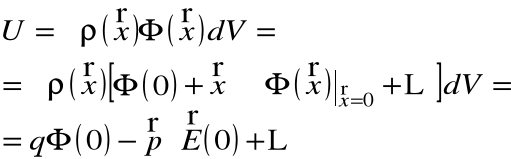
Ta sama metoda może być wykorzystana do rozwinięcia potencjału wektorowego pola magnetycznego:
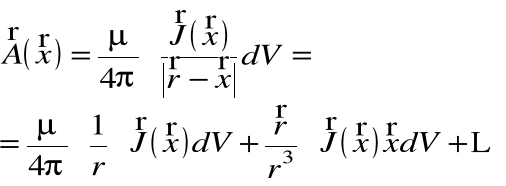
ze względu na to, że potencjał [pola magnetycznego jest wielkością wektorową musimy zastosować pewien trik matematyczny wykorzystujący całkowanie przez części. Dla dwóch arbitralnie wybranych funkcji f i g otrzymujemy:
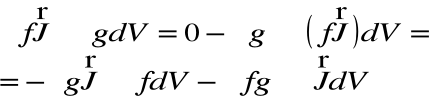
gdzie całkowanie obejmuje całą przestrzeń a gęstości prądu znikają w nieskończoności. Po przeniesieniu całek na jedną stronę otrzymujemy:
![]()
Podstawiając ![]()
i biorąc ![]()
oraz ![]()
otrzymujemy:
![]()
znika potencjał monopolowy
z kolei dla![]()
oraz ![]()
otrzymujemy:
![]()
lub inaczej:
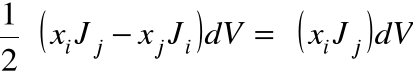
Zastosujmy powyższe wnioski do potencjału wektorowego, otrzymamy wówczas:
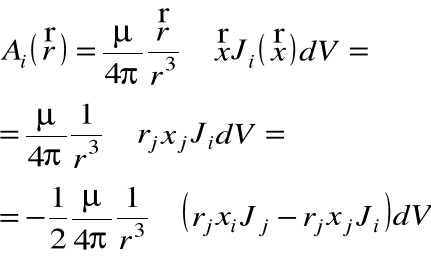
czyli dla wszystkich współrzędnych:
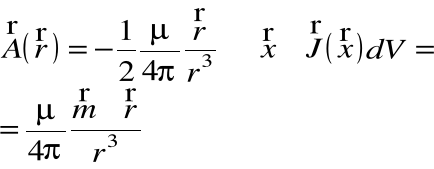
Pole magnetyczne można znaleźć z rotacji potencjału wektorowego:
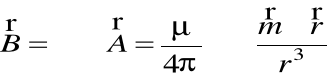
dla jednej współrzędnej wyniesie ono:
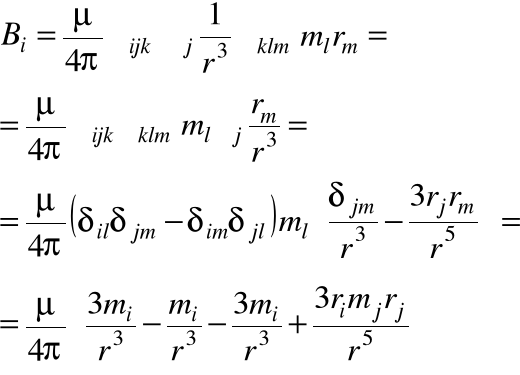
Czyli
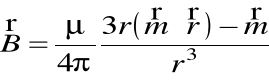
równanie to przypomina składnik pola elektrostatycznego pochodzącego od dipola p.
Wykorzystując potencjał wektorowy można znaleźć wartość siły magnetycznej:
Wykorzystując potencjał wektorowy można znaleźć wartość siły magnetycznej:
![]()
Czyli dla pojedynczej współrzędnej
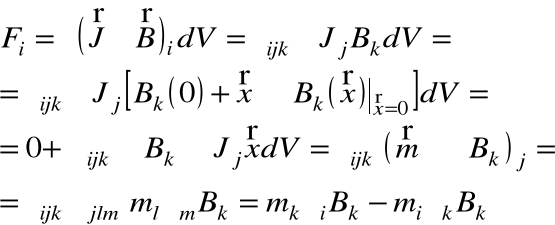
Czyli
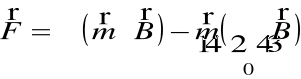
Z zachowawczości sił wynika energia dipola magnetycznego w polu magnetycznym
![]()
gdzie ![]()
jest kątem pomiędzy dipolem a lokalnym polem.
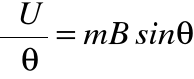
co prowadzi w konsekwencji do ustawiania się dipoli wzdłuż linii pola na skutek powstawania momentu sił
![]()
Na końcu zaważmy, ze powyższe obliczenia były przeprowadzane przy założeniu, że odległości są dużo większe od rozmiarów samych źródeł.
Wyszukiwarka
Podobne podstrony:
Sciaga fiza 2 kolo teoria, Studia, Informatyka (PG Gdańsk), Fizyka, Materiały, Pomoce naukowe
Napędy taśm magnetycznych, Studia, Informatyka, Informatyka, Informatyka
fizyka (2 str), Pomoce naukowe, studia, fizyka
system informatyczny dla ośrodka szkolenia kierowców, Pomoce naukowe, studia, informatyka
Fizyka 2 kolokwim, ATH - studia informatyka, Semestr II, Fizyka
roÂliny-ko-o, Studia, III rok, III rok, V semestr, pomoce naukowe, do egzaminu
warzywa kolo- wersja do nauki, Studia, III rok, III rok, V semestr, pomoce naukowe, do egzaminu
fizyka Ikolokwium, pomoce naukowe
ro-Âciaga-calosc, Studia, III rok, III rok, V semestr, pomoce naukowe, do egzaminu
wyklady I, Studia, III rok, III rok, V semestr, pomoce naukowe, do egzaminu
wyklad-lilie, Studia, III rok, III rok, V semestr, pomoce naukowe, do egzaminu
wyklad-roze, Studia, III rok, III rok, V semestr, pomoce naukowe, do egzaminu
P¦DY DO ROZPOZNAWANIA, Studia, III rok, III rok, V semestr, pomoce naukowe, do egzaminu
SADOWNICTWO -poprawione, Studia, III rok, III rok, V semestr, pomoce naukowe, do egzaminu
kolo-doniczkowe, Studia, III rok, III rok, V semestr, pomoce naukowe, do egzaminu
warzywa odmiany, Studia, III rok, III rok, V semestr, pomoce naukowe, do egzaminu
ro-zestawy, Studia, III rok, III rok, V semestr, pomoce naukowe, do egzaminu
ROŽLINY OZDOBNE Âci-ga 1 kolo, Studia, III rok, III rok, V semestr, pomoce naukowe, do egzaminu
więcej podobnych podstron