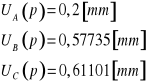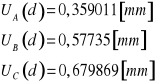II. Podstawy teoretyczne (interferencja).

1) Doświadczenie Younga

Wykazanie, przez Thomasa Younga (w 1801 r.) istnienia interferencji dla światła było pierwszym eksperymentem wskazującym na falowy charakter światła.

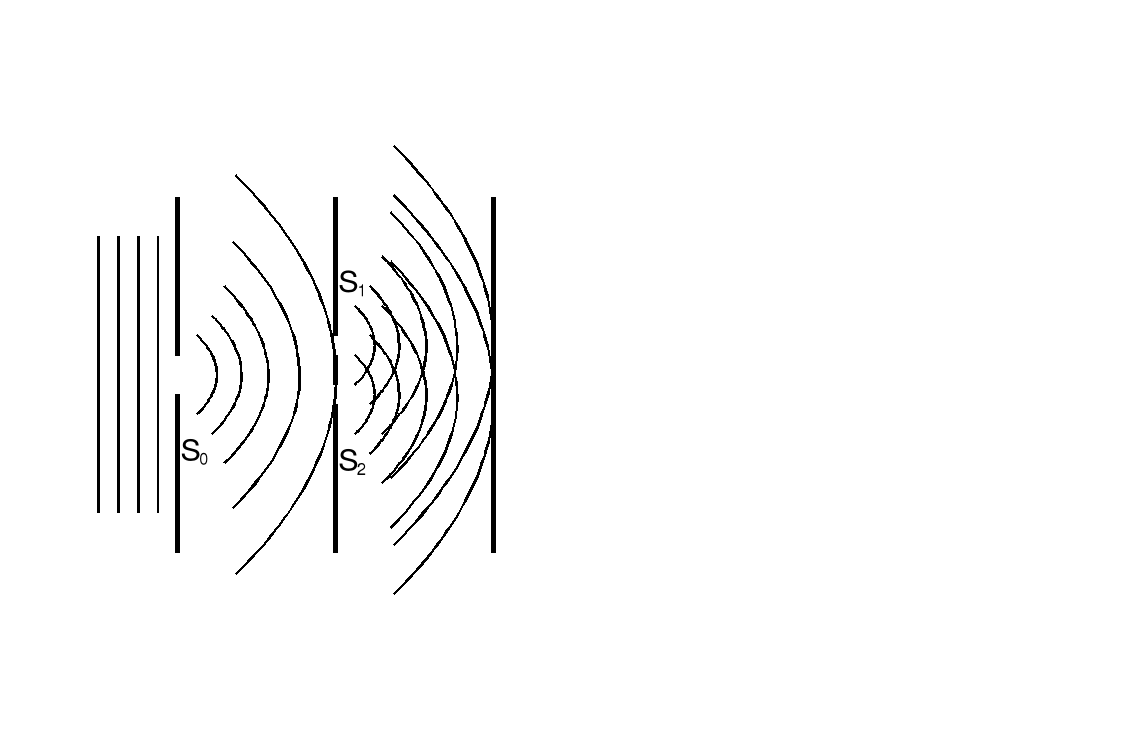
Young oświetlił światłem słonecznym ekran, w którym był zrobiony mały otwór S₀. Przechodzące światło padało następnie na drugi ekran z dwoma otworami S₁ i S₂ i rozchodzą się dalej dwie, nakładające się fale kuliste tak jak na rysunku. Warunki stosowalności optyki geometrycznej nie są spełnione i na szczelinach następuje ugięcie fal. Mamy do czynienia z optyką falową. Jeżeli umieścimy ekran w jakimkolwiek miejscu, tak aby przecinał on nakładające się na siebie fale to możemy oczekiwać pojawienia się na nim ciemnych i jasnych plam następujących po sobie kolejno.

Przeanalizujmy teraz doświadczenie Younga ilościowo.

Zakładamy, że światło padające zawiera tylko jedną długość fali (jest monochromatyczne). Na rysunku poniżej punkt P jest dowolnym punktem na ekranie, odległym o r₁ i r₂ od wąskich szczelin S₁ i S₂.

Linia S₂b została poprowadzona tak, aby PS₂ = Pb. Trzeba zwrócić uwagę, że stosunek d/D przedstawiony na rysunku jest dla większej jasności przesadnie duży. Naprawdę d << D i wtedy kąt S₁S₂b jest równy θ z dużą dokładnością.

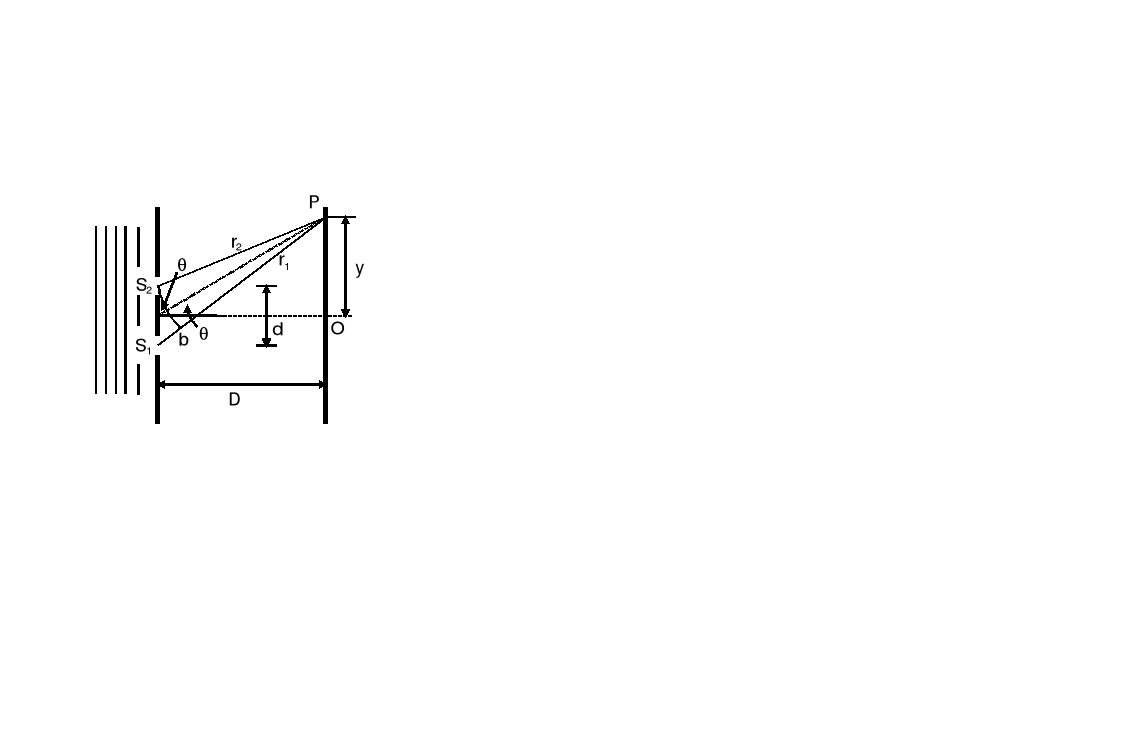
Oba promienie wychodzące ze szczelin S₁ i S₂ są zgodne w fazie, gdyż pochodzą z tego samego czoła fali płaskiej. Jednak drogi, po których docierają do punktu P są różne, więc i ich fazy mogą być różne. Odcinki Pb i PS₂ są identyczne, więc o różnicy faz decyduje różnica dróg optycznych tj. odcinek S₁b. Aby w punkcie P było maksimum to odcinek S₁b musi zawierać całkowitą liczbę długości fal. Jest tak dlatego, że po przebyciu odcinka równego λ faza fali powtarza się więc dla drogi mλ fala ma fazę taką jak na początku tej drogi; odcinek S₁b nie wpływa na różnicę faz a ponieważ fale były zgodne w źródle (szczeliny S₁ i S₂) więc będą zgodne w fazie w punkcie P.

2. Koherencja

Podstawowym warunkiem powstania dobrze określonego obrazu interferencyjnego jest, aby fale świetlne, które przybywają z punktów S₁ i S₂ miały dokładnie określoną różnicę faz ϕ stałą w czasie. Np. jest miejsce na ekranie, dla którego różnica faz wynosi π co oznacza fizycznie, że fale docierające tam wygaszają się (przy założeniu tej samej amplitudy); mamy ciemny prążek. I tak jest zawsze o ile różnica faz się nie zmieni. Gdyby taka zmiana nastąpiła to w tym miejscu natężenie światła nie będzie już równe zeru. Warunkiem stabilności obrazu jest więc stałość w czasie różnicy faz fal wychodzących ze źródeł S₁ i S₂. Mówimy, że te źródła są koherentne czyli spójne.

III. Obliczenia i szacowanie niepewności pomiarowych.

Lp.

1

142

0,2

0,04

2

143

-0,8

0,64

3

141

1,2

1,44

4

142

0,2

0,04

5

143

-0,8

0,64

6

142

0,2

0,04

7

142

0,2

0,04

8

142

0,2

0,04

9

143

-0,8

0,64

10

142

0,2

0,04

Lp.

1

740

1,8

3,24

2

742

-0,2

0,04

3

743

-1,2

1,44

4

741

0,8

0,64

5

740

1,8

3,24

6

743

-1,2

1,44

7

742

-0,2

0,04

8

743

-1,2

1,44

9

742

-0,2

0,04

10

742

-0,2

0,04

Lp.
1	3	5,24	2,24	-0,112	0,012544
2	3,08	5,22	2,14	-0,012	0,000144
3	3,06	5,15	2,09	0,038	0,001444
4	3,05	5,19	2,14	-0,012	0,000144
5	3,04	5,21	2,17	-0,042	0,001764
6	3,13	5,17	2,04	0,088	0,007744
7	3,04	5,17	2,13	-0,002	0,000004
8	3,07	5,11	2,04	0,088	0,007744
9	3,03	5,22	2,19	-0,062	0,003844
10	3,08	5,18	2,1	0,028	0,000784

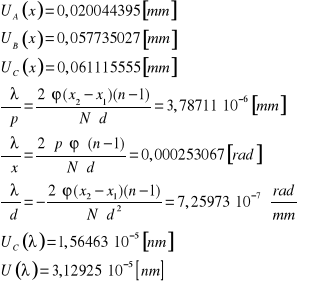
IV. Wnioski:

- nie dokładność pomiaru wynika w dużej mierze z bezwładności i zmęczenia oka

- dzięki bipryzmatowi Fresnela możemy wyznaczać długość fali różnych źródeł światła