WYDZIAŁ ZARRRRZĄDZANIA

I PODSTAW TECHNIKI

W.T.4.1.

1.Agnieszka Baran

2.Bielecka Barbara

3.Sławomir Depta

4.Gardyga Konrad

5.Szałata Jarosław

LABORATORIUM ELEKTROTECHNIKI

ĆWICZENIE NR 2

TEMAT: POMIARY REZYSTANCJI, INDUKCYJNOŚCI I POJEMNOŚCI.

1. Rezystancja.

Zasadniczą rolę w obwodach elektrycznych odgrywają przewodniki metalowe, z których wykonuje się przemysłowe linie energetyczne, instalacje elektryczne, elementy grzejne w odbiornikach, itp.

Rezystancja przewodnika metalowego w zależności od wymiarów geometrycznych i rodzaju materiału wynosi:

gdzie:

l-długość przewodnika,[m];

S-pole przekroju poprzecznego przewodnika,[mm²];

q-rezystywność (opór właściwy ),
;

γ-konduktywność (przewodność właściwa ),
.

Rezystywność jest to cecha materiału z którego wykonany jest przewodnik i jest to rezystancja w Ω przewodnika o długości 1m. i przekroju 1mm².

Rezystancja przewodników metalowych wraz ze wzrostem temperatury rośnie;

gdzie:

R_t-rezystancja przewodnika w temperaturze t,

R₀-rezystancja przewodnika w temperaturze początkowej t₀,

α-temperaturowy współczynnik rezystancji.

Temperaturowy współczynnik rezystancji określa względną zmianę rezystancji przewodnika przy zmianie temperatury o 1°C.

1. pomiar rezystancji małych

Dla dwóch przewodników C1 iC2uformowanych w postaci dwóch cewek jednowarstwowych o danej liczbie zwojów 100 i 100, średnicy cewki 60mm i średnicy drutu odpowiednio 0,95 i 0,52 mm, mierzmy ich rezystancje mostkiem Thomsona i porównujemy rezystancjami obliczonymi wg wzoru:

CEWKA	Liczba zwojów	Średnica cewki	Średnica drutu	Materiał
		-	mm	mm	-
C1	135	60	0,7	Cu
C2	100	60	0,6	Cu

CEWKA	Wyniki pomiarów			Wartość średnia	Obliczona z danych
		I	II			III
		Ω	Ω	Ω	Ω	Ω
C1	1,2	1,2	1,2	1,2	1,16
C2	1,4	1,4	1,4	1,4	1,2

l₁=Π*60*135*10^-3;

l₂=Π*60*100*10^-3;

S₁=∏*d²/4=∏*(0,7)²/4;

S₂=∏*d²/4=∏*(0,6)²/4;

R₁=∏*60*135*10^-3*4/56*∏*(0,7)²=1,16Ω

R₂=∏*60*100*10^-3*4/56*∏*(0,6)²=1,2Ω

Jeżeli chodzi o cewkę pierwszą to różnica między wartością średnia a obliczoną jest niewielka. Spowodowanie to mogło być niedokładnym odczytem z miernika. Natomiast w cewce drugiej różnica między wartością średnią a obliczoną jest znaczna. Spowodowane może być to nieprecyzyjnym wykonaniem pomiaru.

2. pomiar rezystancji dużych

Pomiar rezystancji jednego opornika dokonujemy trzema metodami:

-miernikiem RLC z odczytem cyfrowym,

-technicznym mostkiem Wheatstone'a,

-metodą techniczna.

Pomiary wykonujemy dla trzech wartości napięcia zasilającego nastawionych autotransformatorem AT.

Miernik RLC	Mostek Wheatston'a	Metoda techniczna
RX	RX	U	I	RX	RXśr
Ω	Ω	V	A	Ω	Ω
157	158	60	0,38	157,9	159,5
				30		0,18	166,7
				40		0,26	153,8

R_x obliczamy z prawa Ohma:

R_x1=60/0,38=157,9Ω

R_x2=30/0,18=166,7Ω

R_x3=40/0,26=153,8Ω

Wykorzystanie metody pod względem pracochłonności można przedstawić w tej samej kolejności lak są w tabelce (ostatniej). Najbardziej pracochłonna z całą pewnością jest metoda techniczna, ponieważ wyniki otrzymujemy metodą pośrednią (po odczytaniu wielkości napięcia i natężenia rezystancję trzeba samodzielnie wyliczyć).

3. wyznaczanie temperatury cewki nagrzanej z przyrostu rezystancji

Do próby wykorzystujemy cewkę uzwojoną drutem miedzianym.

Autotransformatorem nastawiamy prąd w obwodzie około 1,2 In (In-prąd znamionowy cewki) i nagrzewamy cewkę przez około 10min.

Stan cewki	U	I	P	R	t
		V	A	W	Ω	°C
Zimny (temp. otoczenia)	252	1	88	88	22
nagrzany	256	1	100	100	57

Rezystancję R obliczamy ze wzoru:

i po przekształceniu:

R₀=88/1²=88Ω

R_t=100/1²=100Ω

Temperaturę nagrzanego uzwojenia wyliczamy ze wzoru:

Temperaturowy współczynnik rezystancji dla miedzi wynosi:

t=100-88/0,0039*88+22=57^oC

2. Indukcyjność

Indukcyjność własna cewki określa zależności:

gdzie:

L-indukcyjność własna cewki,[H];

z-liczba zwojów cewki;

Rμ-reluktancja obwodu magnetycznego,

Reaktancja cewki:

Dla cewki powietrznej, rezystancja wynika z zależności:

jest praktycznie rezystancją przewodu uzwojenia cewki:

1. pomiar indukcji

Pomiar indukcji cewki bez rdzenia wykonujemy dla trzech różnych liczb zwojów miernikiem technicznym.

Cewka	Liczba zwojów	Metoda techniczna								Miernik RLC
				U	I	P	cosϕ	Z	R	XL	L	L
				V	A	W	-	Ω	Ω	Ω	H	H
	Bez rdzenia	4400	100	0,56	22	0,39	178,6	69,7	162,5	0,52	-
		4800	100	0,46	17	0,37	217,4	80,4	202,2	0,64	-
		5200	100	0,4	13	0,33	250	82,5	235	0,75	-

cosφ₁=22/100*0,56=0,36

cosφ₂=0,37

cosφ₃=0,33

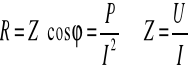
Z₁=100/0,56=178,6Ω

Z₂=217,4Ω

Z₃=250Ω

R₁=Z_1*cosϕ₁=178,6*0,39=69,7Ω

R₂=Z_2*cosϕ₂=80,4Ω

R₂=Z_3*cosϕ₃=82,5Ω

ϕ_1­=arc cosϕ₁=0,91

X_L=U₁/I₁sinφ₁=100/0,56*0,91=162,5Ω

Φ₂=arc cosφ₂=0,93

X_L=U₂/I₂sinφ₂=100/0,46*0,93=202,2Ω

Φ₃=arc cosφ₃=0,94

X_L=U₃/I₃sinφ₃=100/0,4*0,94=235Ω

L=X_L/2Πf

f=50Hz

L₁=X_L1/2Πf=162,5/2Π50=0,52H

L₂=X_L2/2Πf=0,64H

L3=XL3/2Πf=0,75H

Sprawdzamy warunek
porównując stosunki indukcyjności wynikające z danych liczb zwojów cewki ze stosunku tych indukcyjności uzyskanych pomiarów metodą techniczną.

L_max/L_min=(Z_max/Z_min)²

0,75/0,52=250/178,6

1,4=1,39

Popełnione przez nas błędy spowodowane były niedokładnym odczytem wskazań przyrządów a także zaokrągleniem obliczeń do drugiego miejsca po przecinku. Większą dokładność mogliśmy uzyskać zaokrąglając uzyskiwane przez nas wyniki do 5-6 cyfr po przecinku.

3. Pojemność

Kondensator jest to urządzenie elektryczne składające się z dwóch przewodników metalowych odizolowanych dielektrykiem. Kondensator ma zdolność gromadzenia ładunków elektrycznych. Napięcie zasilające U, ładunek q, i pojemność kondensatora C powiązane są zależnością:

Pojemność kondensatora może być zmierzona bezpośrednio lub wyznaczona metodami pośrednimi.

Do pomiarów bezpośrednich stosuje się mierniki RLC, natomiast pośrednio, na podstawie pomiarów napięcia przemiennego o znacznej częstotliwości i natężenia prądu płynącego przez kondensator:

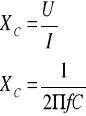
1. pomiary pojemności

Wykonujemy pomiary dwóch kondensatorów metoda techniczną.

Kondensator	Metoda techniczna				Miernik RLC	Pojemność dana
		U	I	XC	C	C	C
		V	A	Ω	μF	μF	μF
C1	100	0,88	113,6	28	-	28
C2	100	0,38	263,2	12,1	-	12

Błąd dopuszczalny poj. Kondensatora wynosi 10%

X_c1=U₁/I₁=100/0,88=113,6Ω

X_c2=U₂/I₂=100/0,38=263,2Ω

C₁=1/35670,4=28μF

C₂=12,1μF

Jak widać pojemność kondensatora uzyskana metodą techniczną w sposób pośredni ma wartość zbliżona do pojemności na kondensatorach. Różnica jest wynikiem błędu jaki popełniamy podczas odczytu z mierników, a także błędu popełnionego podczas liczenia.

Nie jesteśmy w stanie przeprowadzić pomiarów w ten sposób by wartość pojemności uzyskana metodą pośrednią była taka sama jak wartość dana.

---