WPROWADZENIE DO SYSTEMÓW TELEKOMUNIKACYJNYCH
Seminarium
Rok akad.: 2000/2001
Małgorzata Gronicka
![]()
![]()
ZADANIE 3/6
Dla sygnału zmodulowanego częstotliwościowo znaleźć widmo, moc fali nośnej i wstęg bocznych jeśli sygnał modulujący ma postać:
Fala nośna f0=A0cosω0t
Wstęp teoretyczny:
Modulacja częstotliwości (FM) jest postacią modulacji kąta, w której częstotliwość chwilowa jest proporcjonalna do zmian sygnału modulującego.
![]()
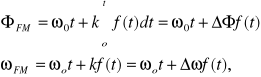
gdzie
ΔΦf(t)-dewiacja fazy,
Δωf(t)-dewiacja częstotliwości.
Całkowita moc sygnału wyraża się wzorem
Pc=P0+2PB=A02/a
gdzie:
P0-moc składowej sygnału zmodulowanego,
PB-moc wstęg bocznych.
Rozwiązanie:
Trygonometryczny szereg Fouriera otrzymuję w sposób pośredni tzn. poprzez różniczkowanie badanego przebiegu i uzyskanie w ten sposób zespolonej postaci szeregu Fouriera.
-k2ωmFk=![]()
+![]()
![]()
Fk= ![]()
Postać wykładnicza
f(t)=![]()
Przechodzę na postać trygonometryczną szeregu Fouriera.
f(t)= ![]()
,
gdzie:
ak= Fk+F-k,
bk= Fk-F-k.
Obliczam ak oraz bk dla k=1,2,3.W wyniku otrzymuję następującą postać funkcji:
f(t)= ![]()
sFM=A0cos(ω0t+k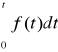
))
sFM=A0cos(ω0t+k(![]()
))
Przyjmuję dane:
k=π,
a=π2,
A0=3.
Podstawiam dane i obliczam β.
β1=8
β2=0,3
Obliczam moce.
Pc=A02/2=4,5 W
Jo(β1)=0,2
J0(β2)=0,95
Po=A0J02(β1)J02(β2)=0,16245 W
PB=Pc-P0=4,33755 W
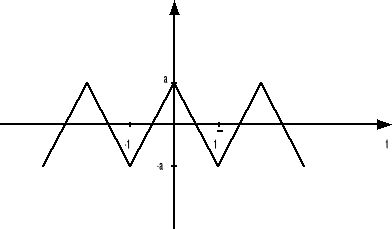
f(t)
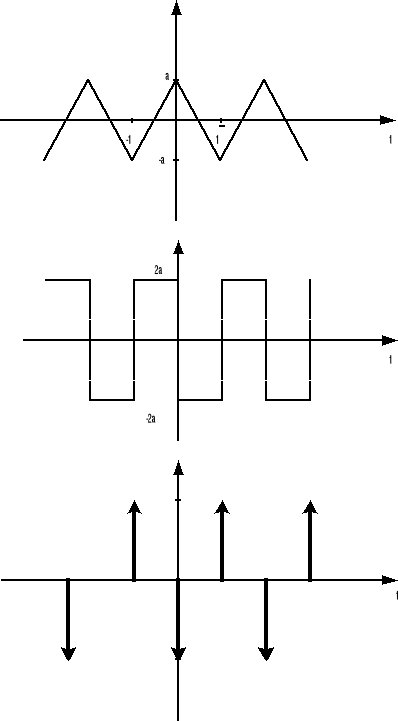
f(t)
f′(t)
f″(t)
-4a
4a
ω
ω0+3ωm
ω0+ωm
ω0-3ωm
ω0-ωm
ω0
Wyszukiwarka
Podobne podstrony:
z4 06, SPRAWOZDANIA czyjeś
z3 01, SPRAWOZDANIA czyjeś
z3 01a, SPRAWOZDANIA czyjeś
Z3 05a, SPRAWOZDANIA czyjeś
Z3 09, SPRAWOZDANIA czyjeś
z3 07, SPRAWOZDANIA czyjeś
Z1 06, SPRAWOZDANIA czyjeś
Z3 03, SPRAWOZDANIA czyjeś
z3 04, SPRAWOZDANIA czyjeś
z3 02 pg, SPRAWOZDANIA czyjeś
pomoc2cd(1), SPRAWOZDANIA czyjeś
Budowa kontenera C, SPRAWOZDANIA czyjeś
Zalety systemów SDH, SPRAWOZDANIA czyjeś
Hartowanie i odpuszczanie, SPRAWOZDANIA czyjeś
z 1 7 a, SPRAWOZDANIA czyjeś
Zabezpieczenie transformatora za pomocą zespołu automatyki(1), SPRAWOZDANIA czyjeś
więcej podobnych podstron