WPROWADZENIE DO SYSTEMÓW TELEKOMUNIKACYJNYCH
Seminarium semestr zimowy 2000/2001
Prowadzący: dr inż. Wojciech Krzysztofik
Michał Zubrzycki (95466)
Zadanie Z3/9
Treść zadania
Sygnał ![]()
; ![]()
; ![]()
, po przejściu przez filtr dolnoprzepustowy i przesuwnik fazy jest grupą falową, która moduluje częstotliwościowo falę nośną ![]()
. Stała modulatora k=180π. Obliczyć amplitudę i moc prążka o częstotliwości fali nośnej sygnału zmodulowanego.
Jn(β) |
|||||||
n β |
0,255 |
0,4 |
0,8 |
0,9 |
1,8 |
3,6 |
7,2 |
0 |
0,99 |
0,96 |
0,85 |
0,81 |
0,34 |
-0,39 |
0,29 |
1 |
0,11 |
0,20 |
0,37 |
0,41 |
0,58 |
0,09 |
-0,05 |
2. Wstęp teoretyczny
Przy modulacji grupą falową (sumą M drgań harmonicznych o dowolnych pulsacjach i amplitudach) faza funkcjonału modulacji ma postać:
![]()
,
gdzie ![]()
- cząstkowy wskaźnik modulacji.
Sygnał zmodulowany wyraża się wzorem:
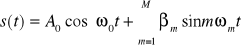
Można to przekształcić do postaci:
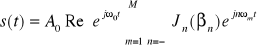
W widmie sygnału zmodulowanego zawarta jest fala nośna, której amplituda wyznaczona jest przez iloczyn funkcji Bessela zerowego rzędu od wszystkich cząstkowych wskaźników modulacji:
![]()
Amplituda fali nośnej jest podwojoną wartością zerowego współczynnika szeregu Fouriera:
![]()
A z twierdzenia Parsevala moc fali nośnej wynosi:
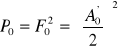
3. Rozwiązanie
Sygnał v(t) można przestawić w postaci trygonometrycznego szeregu Fouriera:
![]()
współczynniki szeregu:
a0=F0=0
an=Fn+F-n
bn=j(Fn-F-n)
wzór ogólny na współczynniki:
![]()
, ![]()
stąd otrzymujemy:
![]()
Po przejściu przez filtr dolnoprzepustowy o transmitancji H1(ω) pozostaną tylko składowe sygnału o pulsacji mniejszej od 380:
![]()
Po przejściu przez przesuwnik fazy o transmitancji H2(ω):
![]()
czyli korzystając z zależności trygonometrycznych otrzymujemy równanie grupy falowej:
![]()
Grupa falowa po przejściu przez modulator FM ma postać:
![]()
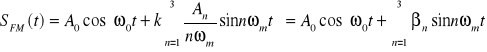
Amplituda fali nośnej jest wyznaczona przez iloczyn funkcji Bessela zerowego rzędu od wszystkich cząstkowych wskaźników modulacji.
![]()
Cząstkowy wskaźnik modulacji:
![]()
Czyli dla k=180π:
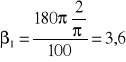
, 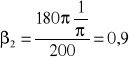
, 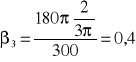
Wartości funkcje Bessela zerowego rzędu dla cząstkowych wskaźników modulacji odczytane z tabeli:
![]()
, ![]()
, ![]()
Stąd amplituda zmodulowanej fali nośnej (A0=1):
![]()
Moc zmodulowanej fali nośnej:
![]()
4
![]()
![]()
![]()
![]()
![]()
FDP
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Modulator
FM
v(t)
z(t)
f(t)
Wyszukiwarka
Podobne podstrony:
z3 06, SPRAWOZDANIA czyjeś
z3 01, SPRAWOZDANIA czyjeś
z3 01a, SPRAWOZDANIA czyjeś
Z3 05a, SPRAWOZDANIA czyjeś
z3 07, SPRAWOZDANIA czyjeś
z5 09, SPRAWOZDANIA czyjeś
Z3 03, SPRAWOZDANIA czyjeś
z2 09, SPRAWOZDANIA czyjeś
z3 04, SPRAWOZDANIA czyjeś
z3 06, SPRAWOZDANIA czyjeś
z3 02 pg, SPRAWOZDANIA czyjeś
pomoc2cd(1), SPRAWOZDANIA czyjeś
Budowa kontenera C, SPRAWOZDANIA czyjeś
Zalety systemów SDH, SPRAWOZDANIA czyjeś
Hartowanie i odpuszczanie, SPRAWOZDANIA czyjeś
z 1 7 a, SPRAWOZDANIA czyjeś
Zabezpieczenie transformatora za pomocą zespołu automatyki(1), SPRAWOZDANIA czyjeś
więcej podobnych podstron