Dawid Trzcionka
91610
WPROWADZENIE DO SYSTEMÓW TELEKOMUNIKACYJNYCH
-SEMINARIUM-
SEM. ZIMOWY 2000/2001
Prowadzący
Dr inż. Wojciech J. Krzysztofik
ZADANIE 3/1
Sygnał f(t)=4sin4π*103t [V] moduluje częstotliwościowo falę nośną c(t)=6cos5π*106t [V]. Szerokość zmodulowanego sFM(t) wynosi B=16kHz. Obliczyć wartość stałej k funkcjonału modulacji. O ile prążków bocznych poszerzy się pasmo, gdy częstotliwość sygnału modulującego zmaleje dwukrotnie?
Wstęp teoretyczny
Sygnał zmodulowany
s(t)=c(t)m[f(t)]
gdzie
c(t) - funkcja nośna
m[f(t)] - funkcjonał modulacji
Funkcjonał modulacji ma postać
![]()
Zatem wyrażenie na sygnał zmodulowany przyjmuje postać
sFM(t)=A0cosΦFM(t)=A0cos(ω0t+*Φsinωt).
*f=*ω/2π=kA dewiacja częstotliwości jest ustalona
*Φ=*ω/ω dewiacja fazy zależy od częstotliwości sygnału modulującego
Po wprowadzeniu pojęcia wskaźnika modulacji β
β=*ω/ω=*f/f przy modulacji FM
wyrażenie na sygnał zmodulowany kątowo zapisujemy
sFM(t)=A0cos(ω0t+βsinωt).
Rozwiązanie zadania
Dane: Szukane:
f(t)=4sin4π*103t [V] k=?
c(t)=6cos5π*106t [V]
B=16kHz dla sFM(t)
ω=2πf
ff=103 [Hz] - częstotliwość sygnału modulującego
fc=106 [Hz] - częstotliwość fali nośnej
β=*ω/ω=kA/ω
Szerokość pasma sygnału FM można oszacować
B=2f(β+1)=2f(kA/ω+1).
Podstawiając wartości
ω=4π*103
A=4
f=ω/2π=2*103 Hz
B=16kHz=16*103 Hz
Otrzymujemy
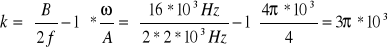
k=3π*103
Jeśli przyjąć, że widmo sygnału jest określone przez wszystkie prążki, których amplituda jest większa niż 5% amplitudy fali nośnej przed modulacją, to między liczbą par uwzględnionych prążków a dewiacją fazy zachodzi następująca zależność
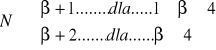
Dla naszych wartości mamy
![]()
Korzystamy z pierwszego przybliżenia
N=β+1=3+1=4
Jeżeli częstotliwość sygnału modulującego zmaleje dwukrotnie:
![]()
N=β+2=6+2=8
Odp. Jeżeli częstotliwość sygnału modulującego zmaleje dwukrotnie, to liczba prążków wzrośnie dwukrotnie.
Wyszukiwarka
Podobne podstrony:
z3 06, SPRAWOZDANIA czyjeś
z3 01, SPRAWOZDANIA czyjeś
Z3 05a, SPRAWOZDANIA czyjeś
Z3 09, SPRAWOZDANIA czyjeś
z3 07, SPRAWOZDANIA czyjeś
Z2 01a, SPRAWOZDANIA czyjeś
Z3 03, SPRAWOZDANIA czyjeś
z3 04, SPRAWOZDANIA czyjeś
z3 06, SPRAWOZDANIA czyjeś
z3 02 pg, SPRAWOZDANIA czyjeś
pomoc2cd(1), SPRAWOZDANIA czyjeś
Budowa kontenera C, SPRAWOZDANIA czyjeś
Zalety systemów SDH, SPRAWOZDANIA czyjeś
Hartowanie i odpuszczanie, SPRAWOZDANIA czyjeś
z 1 7 a, SPRAWOZDANIA czyjeś
Zabezpieczenie transformatora za pomocą zespołu automatyki(1), SPRAWOZDANIA czyjeś
w4m, SPRAWOZDANIA czyjeś
więcej podobnych podstron