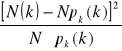Wyniki pomiarów:
Tabela I
Lp |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
1 |
4 |
6 |
11 |
3 |
6 |
2 |
4 |
7 |
9 |
5 |
6 |
3 |
5 |
3 |
7 |
6 |
3 |
4 |
6 |
5 |
2 |
2 |
7 |
4 |
5 |
7 |
5 |
3 |
6 |
3 |
1 |
7 |
4 |
1 |
6 |
3 |
5 |
4 |
5 |
3 |
5 |
3 |
5 |
3 |
7 |
6 |
4 |
9 |
3 |
7 |
8 |
3 |
5 |
2 |
7 |
5 |
8 |
2 |
6 |
8 |
7 |
6 |
4 |
3 |
5 |
8 |
9 |
0 |
5 |
4 |
10 |
4 |
5 |
4 |
7 |
4 |
7 |
6 |
9 |
3 |
4 |
8 |
4 |
5 |
7 |
4 |
2 |
10 |
1 |
4 |
5 |
2 |
12 |
6 |
2 |
5 |
8 |
11 |
5 |
4 |
5 |
4 |
6 |
5 |
6 |
6 |
7 |
6 |
4 |
10 |
6 |
10 |
5 |
7 |
4 |
6 |
4 |
6 |
3 |
7 |
8 |
6 |
5 |
3 |
3 |
7 |
2 |
5 |
2 |
5 |
3 |
9 |
5 |
4 |
12 |
3 |
7 |
3 |
9 |
5 |
8 |
2 |
7 |
9 |
2 |
4 |
8 |
1 |
6 |
4 |
8 |
9 |
7 |
3 |
11 |
7 |
8 |
5 |
9 |
1 |
7 |
6 |
6 |
5 |
1 |
5 |
6 |
9 |
7 |
4 |
3 |
4 |
7 |
10 |
6 |
5 |
6 |
5 |
3 |
6 |
7 |
6 |
4 |
3 |
4 |
5 |
4 |
4 |
10 |
5 |
8 |
7 |
5 |
8 |
3 |
11 |
2 |
4 |
6 |
4 |
5 |
4 |
2 |
5 |
4 |
6 |
3 |
6 |
3 |
Tabela II
Lp |
N t = 100 s |
N t = 200 s |
N t = 500 s |
1 |
3881 |
14166 |
35169 |
2 |
3916 |
14455 |
35457 |
3 |
3793 |
14206 |
35638 |
4 |
3827 |
14181 |
35217 |
5 |
3863 |
14361 |
35196 |
Tabela III
Lp |
Nt t = 100 s |
Nt t = 200 s |
Nt t = 500 s |
1 |
93 |
43 |
128 |
2 |
25 |
27 |
176 |
|
59 |
35 |
152 |
Opracowanie wyników pomiarów.
Dla pomiarów z tabeli I obliczam ilość N(k) i częstość p(k) pomiarów, dla których liczba zliczeń wynosi k:
![]()
gdzie N - całkowita liczba pomiarów (N = 200)
![]()
![]()
Wyznaczam średnią liczbę zliczeń w pomiarze k według wzoru:
![]()
![]()
![]()
Z rozkładu Poissona obliczam prawdopodobieństwo pk(k) według wzoru:

![]()
![]()
Wyniki wszystkich obliczeń zestawiam w tabeli IV.
Tabela IV
k |
N(k) |
p(k) |
pk(k) |
0 |
1 |
0,005 |
0,00499 |
1 |
6 |
0,03 |
0,02645 |
2 |
13 |
0,065 |
0,07001 |
3 |
26 |
0,13 |
0,12382 |
4 |
33 |
0,165 |
0,16401 |
5 |
35 |
0,175 |
0,17390 |
6 |
30 |
0,15 |
0,15361 |
7 |
24 |
0,12 |
0,11631 |
8 |
12 |
0,06 |
0,07705 |
9 |
9 |
0,045 |
0,04537 |
10 |
5 |
0,025 |
0,02405 |
11 |
4 |
0,02 |
0,01159 |
12 |
2 |
0,01 |
0,00512 |
Dla pomiarów z tabeli II obliczam:
Bezwzględny kwadratowy błąd statystyczny natężenia dla każdego pomiaru bez uwzględnienia tła:
![]()
gdzie ![]()
np.: dla t=100 s
![]()
Bezwzględny kwadratowy błąd statystyczny natężenia dla każdego pomiaru z uwzględnieniem tła:
![]()
np.: dla t=100 s
![]()
Względny kwadratowy błąd statystyczny natężenia dla każdego pomiaru bez uwzględnienia tła:
![]()
np.: dla t=100 s
![]()
Względny kwadratowy błąd statystyczny natężenia dla każdego pomiaru z uwzględnieniem tła:
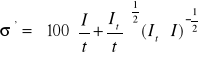
np.: dla t=100 s
![]()
Średni błąd kwadratowy średniej arytmetycznej bez uwzględnienia tła:
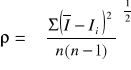
np.: dla t=100 s
w moim przypadku n=5
![]()
n(n-1)=20

Średni błąd kwadratowy średniej arytmetycznej z uwzględnieniem tła:
![]()

![]()
np.: dla t=100 s
![]()
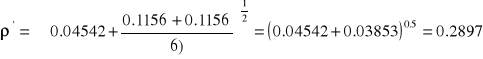
Wyniki wszystkich obliczeń zestawiam w odpowiednich tabelach.
Tabela V - obliczenia dla t = 100 s.
N |
I |
|
|
|
|
3881 |
38,81 |
0,623 |
0,6277 |
1,6052 |
13,1176 |
3916 |
39,16 |
0,626 |
0,6305 |
1,5980 |
13,1171 |
3793 |
37,93 |
0,616 |
0,6206 |
1,6237 |
13,1188 |
3827 |
38,27 |
0,619 |
0,6234 |
1,6165 |
13,1193 |
3863 |
38,63 |
0,622 |
0,6263 |
1,6089 |
13,1188 |
Tabela VI - obliczenia dla t = 200 s.
N |
I |
|
|
|
|
14266 |
71,33 |
0,5972 |
0,5979 |
0,8372 |
16,922 |
14455 |
72,275 |
0,6011 |
0,6019 |
0,8317 |
16,923 |
14206 |
71,03 |
0,5959 |
0,5967 |
0,8390 |
16,924 |
14181 |
70,905 |
0,5954 |
0,5962 |
0,8397 |
16,924 |
14361 |
71,805 |
0,5992 |
0,5999 |
0,8345 |
16,924 |
Tabela VII - obliczenia dla t = 500 s.
N |
I |
|
|
|
|
35169 |
70,338 |
0,3751 |
0,3759 |
0,5332 |
8,1286 |
35457 |
70,914 |
0,3766 |
0,3774 |
0,5311 |
8,1384 |
35638 |
71,276 |
0,3776 |
0,3784 |
0,5297 |
8,1283 |
35217 |
70,434 |
0,3753 |
0,3761 |
0,5329 |
8,1285 |
35196 |
70,392 |
0,3752 |
0,3760 |
0,5330 |
8,1286 |
Tabela VIII
Lp. |
t |
|
|
1 |
100 |
0.21312 |
0.2897 |
2 |
200 |
0.25423 |
0.2553 |
3 |
500 |
0.18303 |
0.1851 |
Stosując test χ2 dokonuję weryfikacji rozkładu doświadczalnego i teoretycznego Poissona. Obliczenia wykonuję teoretycznie.
Hipoteza H0: F(x)![]()
Ω
F(x) - dystrybuanta rozkładu liczby okresów
Ω - klasa wszystkich rozkładów Poissona
Tabela IX
k |
N(k) |
kN(k) |
pk(k) |
N pk(k)
|
|
0 |
1 |
0 |
0,005 |
1 |
0 |
1 |
6 |
6 |
0,026 |
5,2 |
0,1231 |
2 |
13 |
26 |
0,07 |
14,0 |
0,07143 |
3 |
26 |
78 |
0,124 |
24,8 |
0,05806 |
4 |
33 |
132 |
0,164 |
32,8 |
0,00122 |
5 |
35 |
175 |
0,174 |
34,8 |
0,00115 |
6 |
30 |
180 |
0,154 |
30,8 |
0,02078 |
7 |
24 |
168 |
0,116 |
23,4 |
0,0276 |
8 |
12 |
96 |
0,077 |
15,4 |
0,75065 |
9 |
9 |
81 |
0,045 |
9,0 |
0 |
10 |
5 |
50 |
0,024 |
4,8 |
0,0083 |
11 |
4 |
44 |
0,0112 |
2,24 |
1,38286 |
12 |
2 |
24 |
0,005 |
1 |
1 |
Aby sprawdzić hipotezę zerową trzeba porównać sumę 
z wartością odczytaną z tablic dla rozkładu Poissona przy poziomie istotności α= 0,05.
Z tabeli rozkładu χ2 dla n-k-1 stopni swobody, czyli 10 i poziomie istotności α= 0,05 odczytuję wartość krytyczną:
χ2n, α= 21,026
Ponieważ χ2<< χ2n, α a wykres teoretyczny i doświadczalny są porównywalne pozwala mi to na przyjęcie hipotezy zerowej i uznaniu rozkładu otrzymanego w doświadczeniu za rozkład Poissona.
Wnioski.
Na podstawie wykresu można stwierdzić, że jest to rozkład Poissona. Wykres doświadczalny w znacznym stopniu pokrywa się z wykresem teoretycznym, co pozwala uznać ćwiczenie z wykonane poprawnie, a otrzymany wykres za wykres rozkładu Poissona.
17
Wyszukiwarka
Podobne podstrony:
680
680 681
bezpieczeństwo imprez masowych [Dz.U.97.106.680], Licencja Pracownika Ochrony-Różne dokumenty
680
680
680
Dz.U. 1996 nr 146 oz. 680 Tekst ujednolicony
680
680
680
680
680
680
680 put + odp
680
Salvatore R A Drizzt 05 Dolina Lodowego Wichru 02 Strumienie Srebra (SCAN dal 680)
DzU 97 08 22 106 poz 680 o bezpieczeństwie imprez masowych
ROUNDUP MAX 680 SG
więcej podobnych podstron