Ruch drgający.
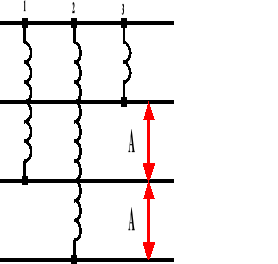
Ciało wychylone z położenia równowagi wykonuje ruch drgający, w którym wyróżniamy:
A - amplituda, jest to największe wychylenie z położenia równowagi;
T - okres, jest to czas jednego pełnego drgnienia;
f - częstotliwość, jest to ilość drgań przypadających na okres czasu.
![]()
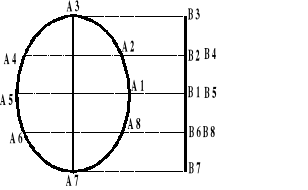
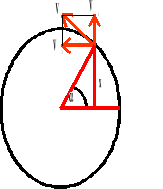
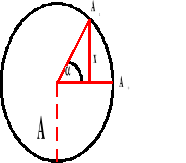
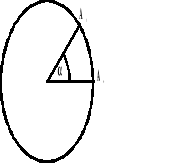
Punkt wykonuje ruch po okręgu, a jego rzut na osi wykonuje ruch drgający.
Faza.
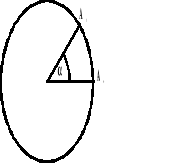
Fazą w ruchu drgającym nazywamy kąt, o który wychyli się punkt z położenia równowagi.
Jeżeli
zakreślono w t
360o zakreślono w T
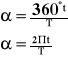
to:
a - zakreślony kąt
t - czas, w którym zakreślono dany kąt
T - okres
Wychylenie.
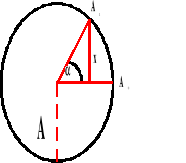
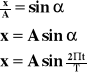
A - amplituda
x - odległość
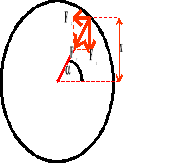
Prędkość.
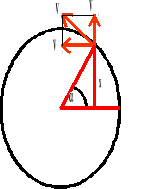
Wektor V1 jest odpowiedzialny za ruch drgający punktu.
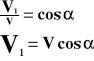
Ale
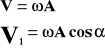
Ale
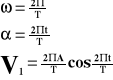
V - prędkość
A - amplituda
T - okres
t - czas
- prędkość kątowa
- kąt
Ruch drgający harmoniczny.
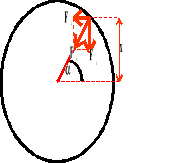
Istotną rolę w ruchu drgającym odgrywa składowy wektor F1, gdyż jest on odpowiedzialny za ruch rzutu punktu na oś.
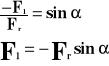
Minus dlatego, bo wektor F1 jest skierowany w dół (umowa).
Ale
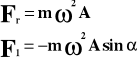
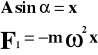
Ale
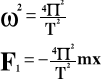
Ale
Ruch drgający harmoniczny, to taki, w którym siła jest wprost proporcjonalna do wychylenia.
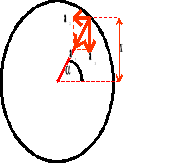
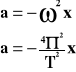
F - siła
A - amplituda
- kąt
m - masa
- przyspieszenie kątowe
T - okres
x - wychylenie
a - przyspieszenie
Wartości maksymalne.
Przyspieszenie:
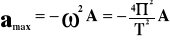
Siła: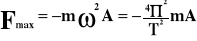
Prędkość:
![]()
A - amplituda
T - okres
F - siła
m - masa
- przyspieszenie kątowe
a - przyspieszenie
V - prędkość
Energia w ruchu drgającym.
Energia kinetyczna:
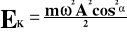
Energia potencjalna: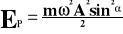
Energia całkowita:
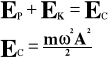
A - amplituda
m - masa
- przyspieszenie kątowe
- kąt
Ep - energia potencjalna
Ek - energia kinetyczna
Ec - energia całkowita
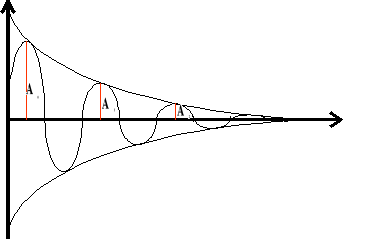
Tłumienie drgań.
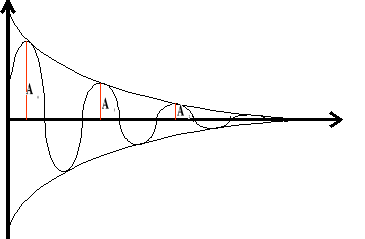
Wykres ruchu drgającego tłumionego.
Tłumienie drgań zachodzi wtedy, gdy ciało (układ) wykonuje ruch drgający, a nie jest zasilany energią zewnętrzną. Amplituda maleje w wyniku oporu (tarcia) ośrodków, w których odbywają się te drgania.
Współczynnik tłumienia wyraża się stosunkiem dwóch sąsiednich amplitud.
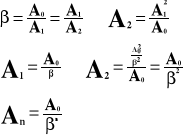
A - amplituda
- współczynnik tętnień
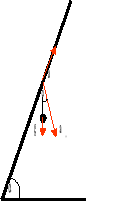
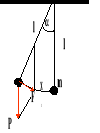
Wahadło matematyczne.
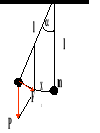
Wahadło matematyczne jest to przyrząd, którego masa skupiona jest w jednym punkcie i zawieszona na nieważkiej nici powyżej środka ciężkości.
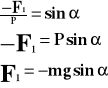
Zakładamy, że wychylenie (x) jest niewielkie, czyli możemy porównać je do odcinka.
![]()
Czyli:
![]()
Powyższy wzór porównujemy ze wzorem na siłę w ruchu drgającym:
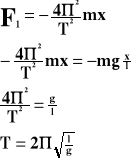
Powyższy wzór przedstawia okres drgań wahadła nieruchomego lub poruszającego się ruchem jednostajnym.
Jak widać okres drgań zależy od długości wahadła (l) i przyspieszenia grawitacyjnego ziemi (g). Nie zależy od masy wahadła i wychylenia.
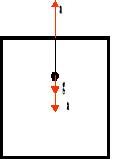
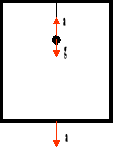
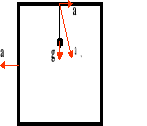
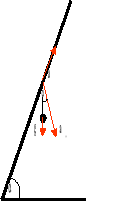
Okres drgań wahadła poruszającego się ruchem jednostajnie przyspieszonym ma postać:
do góry:
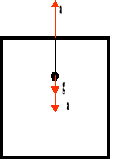
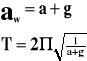
w dół:
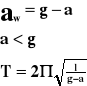
w ruchu poziomym:
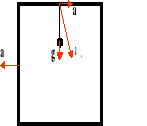
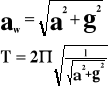
po skosie:
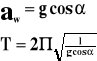
F - siła
P - ciężar właściwy
m - masa ciała
g - przyspieszenie ziemskie
- kąt
x - odchylenie
l - długość
T - okres
a - przyspieszenie
Rezonans mechaniczny.
Rezonans mechaniczny, to takie zjawisko fizyczne, w którym jedno ciało drgające wprawia w ruch drgający drugie ciało (układ ciał).
Fale w ośrodkach sprężystych.
Podział fal ze względu na sposób rozchodzenia się:
Fala podłużna, to taka, w której drgania odbywają się zgodnie z kierunkiem rozchodzenia się fal.
Fala poprzeczna, to taka, w której drgania są prostopadłe do kierunku rozchodzenia się fal.
Podział fal ze względu na kształt:
Fala liniowa, to taka, która rozchodzi się wzdłuż jednego kierunku.
Fala powierzchniowa, to taka, która rozchodzi się wzdłuż dwóch kierunków.
Fala poprzeczna, to taka, która rozchodzi się wzdłuż trzech kierunków.
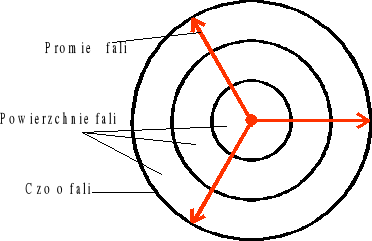
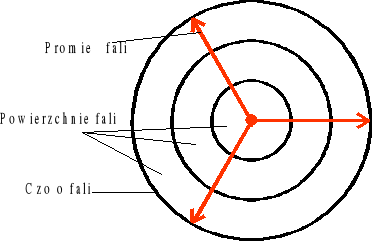
Promieniem fali nazywamy kierunek, w jakim rozchodzi się fala.
Powierzchnie falowe, są to miejsca geometryczne cząstek drgających w tej samej fazie, są one prostopadłe do promieni fali.
Czołem fali nazywamy powierzchnię falową najbardziej oddaloną od źródła.
![]()
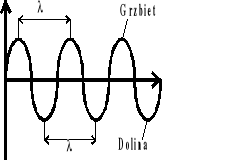
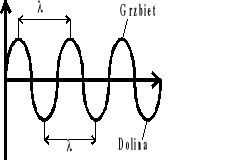
Przez długość fali uważamy najbliższą odległość dwóch punktów drgających w tej samej fazie.
V - prędkość
T - okres
f - częstotliwość
- długość fali
Równanie ruchu falowego.
Fala rozchodzi się w ośrodkach ze skończoną prędkością. Wobec tego, każda cząstka ośrodka wykonuje ruch drgający o innej fazie aniżeli źródło. Ta różnica fal zależy od: odległości cząstek od źródła oraz prędkości fali.
Cząstka będąca źródłem wyraża się wzorem:
![]()
Cząstka znajdująca się w pewnej odległości od źródła, osiągnie tę wartość wychylenia później. W chwili t wychylenie tej cząstki ma wartość:
![]()
x - wychylenie cząstki
A - amplituda
- częstość kołowa
S - odległość cząstki od źródła
V - prędkość
Zasada Huygensa.
Jeśli fala napotka cząstkę zdolną do wykonywania drgań, pobudza ją do drgań - jednocześnie cząstka ta staje się źródłem nowej fali elementarnej. Powstałe w ten sposób fale nakładają się wzajemnie, co prowadzi do obserwowanych powierzchni falowych.
Ta zasada jest słuszna dla wszystkich rodzajów fal.
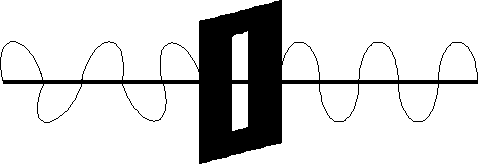
Dyfrakcja.
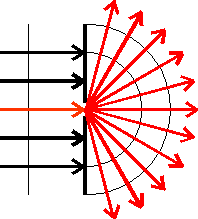
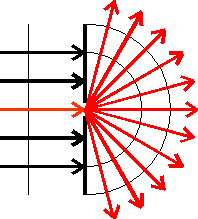
Dyfrakcja czyli ugięcie, czyli odstępstwo od prostoliniowości rozchodzenia się fal.
Jeśli fala napotka ścianę, w której znajduje się otwór (szczelina), wówczas promień przechodzący przez ten otwór rozprzestrzeni się poza nim w kształcie wiązki rozbieżnej.
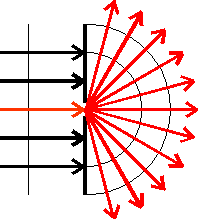
Ogólnie biorąc fala ugina się przechodząc przez otwory, szczeliny itp.
Zjawisko ugięcia możemy wytłumaczyć na podstawie zasady Huygensa.
Kąt między pierwotnym kierunkiem i kierunkiem fali ugiętej nazywamy kątem ugięcia. Energia promienia padającego na szczelinę nie rozkłada się równomiernie, lecz na wszystkie kierunki powstałe w wyniku ugięcia, maleje wraz ze wzrostem kąta ugięcia.
Interferencje.
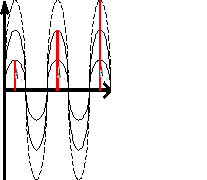
Interferencje, jest to zjawisko polegające na nakładaniu się fal.
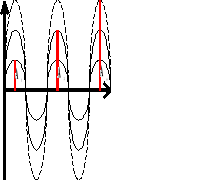
![]()
Gdy fale spotkają się zgodnymi fazami następuje wzmocnienie; powstaje fala wypadkowa, której amplituda równa jest sumie amplitud fal nakładających się na siebie.
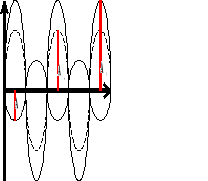
![]()
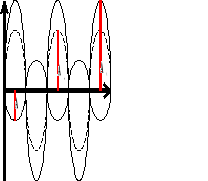
Gdy fale spotkają się przeciwnymi fazami, to amplituda fali wypadkowej równa jest różnicy fal nakładających się na siebie.
A - amplituda
Odbicia fal.
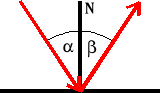
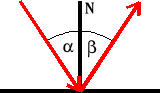
Kąt padania promienia fali jest równy kątowi odbicia, przy czym promienie padający i odbity oraz normalna do powierzchni granicznej leżą w jednej płaszczyźnie.
N - normalna
- kąt padania
- kąt odbicia
Załamania.
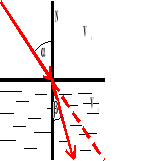
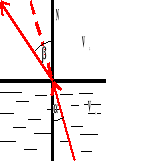
W ośrodkach jednorodnych (o jednakowej gęstości) fale rozchodzą się po liniach prostych.
Ulegają załamaniu, gdy przechodzą przez ośrodki o różnej gęstości.
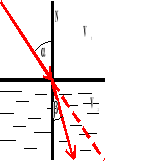
Gdy fala przechodzi z ośrodka rzadszego do gęstszego, ulega załamaniu, przy czym kąt padania jest większy od kąta załamania.
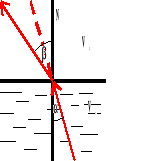
Gdy fala przechodzi z ośrodka gęstszego do rzadszego, ulega załamaniu, przy czym kąt padania jest mniejszy od kąta załamania.
![]()
Stosunek sinusa kąta padania do sinusa kąta załamania jest wielkością stałą i równą stosunkowi prędkości w jednym i drugim ośrodku.
N - normalna
- kąt padania
- kąt odbicia
V - prędkość fali
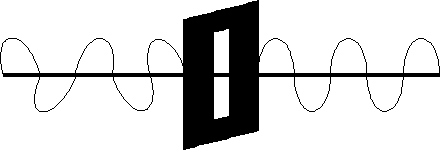
Polaryzacja.
Fala nie spolaryzowana, to taka fala, w której drgania odbywają się w różnych płaszczyznach, a spolaryzowana - w jednej płaszczyźnie.
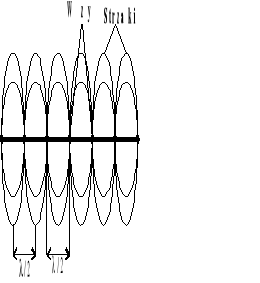
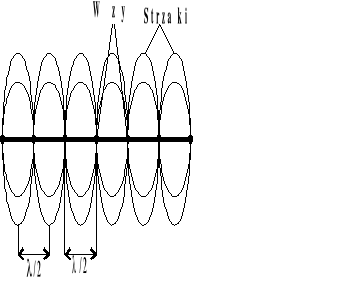
Fala stojąca.
Jeśli fala pada tak, że odbita biegnie wzdłuż tego samego kierunku, wówczas zachodzi nakładanie się fal padających i odbitych, w wyniku czego powstaje stan drgań, który nazywamy falą stojącą. W takim przypadku obserwujemy węzły fali, to jest cząstki, które nie wykonują drgań oraz strzałki, e których cząstki mają największą amplitudę. Odległość między dwoma najbliższymi węzłami (strzałkami) wynosi połowę długości fali.
Drgania i fale mechaniczne
Drgania i fale mechaniczne
22
21
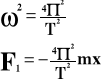
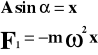
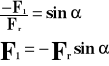
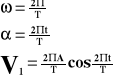
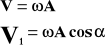
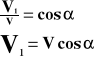
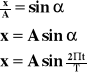
![]()
![]()
![]()
![]()
![]()
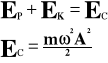
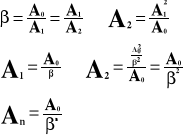
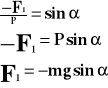
![]()
![]()
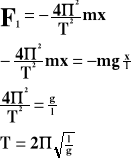
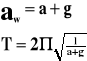
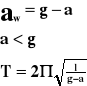
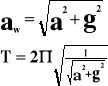
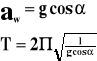
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
OGNIWA (2), Sprawozdania - Fizyka
Ćwiczenie nr 50b, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr50b
Mech- Badanie zależności współczynnika lepkości cieczy od te, Sprawozdania - Fizyka
Doświadczalne spr p. Malusa, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr70
Sprawozdanie Fizyka ćwiczenie 4(M04)
ćw13 sprawozdania fizyka 3, Sprawozdanie
3 W LEPKO CIECZY, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
Pomiar promieni krzywizny soczewki płasko - wypukłej, Sprawozdania - Fizyka
Ćwiczenie nr 82, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr82
PUZON, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki s
Moment Bezwładności, Sprawozdania - Fizyka
Wyznaczanie momentu bezwładności brył za pomocą drgań skrę(1 (2), Sprawozdania - Fizyka
Ćwiczenie nr 65c, sprawozdania, Fizyka - Labolatoria, Ćwiczenie nr65c
test metale tabela, Studia, Ogólne, Fiyzka, od romka, fizyka, sprawozdania fizyka
Bezwladnosc tab, Sprawozdania - Fizyka
Mech- Wyznaczanie ciepła topnienia lodu(1), Sprawozdania - Fizyka
Atom- Wyznaczanie stałej Plancka i pracy wyjścia elektronów(1), Sprawozdania - Fizyka
Sprawozdanie Fizyka ćwiczenie 6(O01)
więcej podobnych podstron