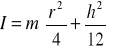Mięsowicz Sławomir
1 CD L 6
LABORATORIUM FIZYCZNE
Temat laboratorium:
Pomiar bezwładności wahadła Maxwella.
I. Zagadnienia wstępne .
W celu opisania ruchu ciał na gruncie mechaniki klasycznej, posługujemy się dwoma pojęciami-modelami: punkt materialny, bryła sztywna.
W ruchu postępowym równania opisujące ruch punktu lub bryły są jednakowe; dla uproszczenia całą bryłę reprezentuje punkt zwany środkiem masy tej bryły.
W ruchu obrotowym, chcąc zachować matematyczne podobieństwo równań opisujących zarówno punkty jak i bryłę sztywną, przyjęto odpowiednie przyporządkowania.
ruch postępowy |
ruch obrotowy |
m - masa |
I - moment bezwładności
|
v - prędkość liniowa |
- prędkość kątowa |
a - przyspieszenie liniowe |
-przyspieszenie kątowe |
F - siła |
M - moment siły |
p - pęd |
K - moment pędu
r - wektorowa odległość przyłożenia siły od osi |
II zasada dynamiki Newtona
|
II zasada dynamiki Newtona
|
Ek - energia kinetyczna
|
Ek - energia kinetyczna
|
Jeżeli oś obrotu nie przechodzi przez środek masy ciała posługujemy się prawem Steinera, elipsoidą bezwładności lub metodami doświadczalnymi. Wykorzystując symetrię niektórych brył można wyliczyć momenty bezwładności względem osi głównych.
kula jednorodna |
|
walec pusty - podłużna oś symetrii |
|
walec pełny - podłużna oś symetrii |
|
walec pełny - poprzeczna oś symetrii |
|
pierścień o promieniu zewnętrznym R i wewnętrznym r - podłużna oś symetrii |
|
Jako układ odosobniony w którym następuje zamiana energii potencjalnej w kinetyczną i na odwrót może posłużyć wahadło Maxwella, które jest krążkiem zamocowanym na osi, zawieszonym bifilarnie na pewnej wysokości h. W tym położeniu krążek ma Ep=m g h .
Uwolniony z podparcia krążek spada pod własnym ciężarem wykonując zarazem ruch obrotowy, a tym samym jego Ek składa się z dwóch członów:
![]()
- energia kinetyczna ruchu postępowego,
![]()
- energia kinetyczna ruchu obrotowego.
Zasada zachowania energii, przy zaniechaniu oporów ruchu, wyraża się więc równaniem:
![]()
[ 1 ]
gdzie: v - prędkość przesuwania się środka masy układu,
- prędkość kątowa w ruchu obrotowym wokół osi krążka,
r - promień krążka,
I - moment bezwładności krążka względem osi obrotu przechodzącej przez środek masy.
Zakładając, że ruch środka masy jest ruchem jednostajnie przyspieszonym, bez prędkości początkowej:
![]()
i ![]()
otrzymujemy związek:
![]()
Przekształcając równanie [ 1 ] względem I i podstawiając do niego z wyżej przytoczonych zależności v i , wyliczymy moment bezwładności wahadła Maxwella: 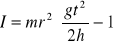
[ 2 ]
Masa m jest sumą masy osi wahadła, masy krążka i masy pierścienia nałożonego na krążek. Z powyższego wzoru można wyznaczyć moment bezwładności wahadła Maxwella mierząc czas opadania t i przebytą w tym czasie drogę h. Za r przyjmujemy promień osi wahadła na którą nawinięta jest nić.
Na wynik obliczeń mają wpływ niedokładności pomiarów jak i brak spełnienia założeń dotyczących zasady zachowania energii, czy tego, że ruch jest ruchem jednostajnie przyśpieszonym.
Moment bezwładności I można obliczyć teoretycznie sumując momenty poszczególnych elementów wahadła.
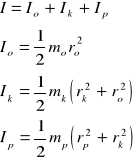
[ 3 ]
gdzie: ro - promień osi wahadła,
rk - promień zewnętrzny krążka,
rp - promień wewnętrzny pierścienia
II. Wykonanie ćwiczenia .
1. Włączyć przyrząd do sieci (W3).
2. Na krążek wahadła nałożyć dowolnie wybrany pierścień dociskając go do oporu.
3. Skręcić na osi wahadła nić zawieszenia i unieruchomić je przy pomocy elektromagnesu (przycisk W2 wyciśnięty).
4. Sprawdzić czy dolna krawędź pierścienia pokrywa się z zerem skali naniesionej na kolumnę. W przypadku nie spełnienia powyższego warunku odkręcić wspornik górny i wyregulować wysokość jego ustawienia.
5. Nacisnąć przełącznik (W1) w celu wyzerowania przyrządu i wcisnąć przełącznik (W2).
6. Odczytać zmierzoną wartość czasu spadania wahadła.
7. Powtórzyć pomiar co najmniej 10 razy.
8. Pomiary powtórzyć dla innego pierścienia.
Dokładność pomiaru przeprowadza się przez wyliczenia następujących wielkości:
![]()
gdzie: Idośw - moment bezwładności wyliczony wg wzoru [ 2 ]
Iteor - teoretyczna wartość momentu bezwładności
m0 [ g ] |
mk [ g ] |
mp [ g ] |
r [ cm ] |
h [ cm ] |
t [ s ] |
Idoś [ kg m2] |
Iteor [ kg m2] |
Δ % |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6
Wyszukiwarka
Podobne podstrony:
Lab fiz 01, fff, dużo
Lab fiz 05, fff, dużo
Lab fiz 24, fff, dużo
Lab fiz 04, fff, dużo
Lab fiz 46, fff, dużo
Lab fiz 22, fff, dużo
Lab fiz 27, fff, dużo
Lab fiz 51, fff, dużo
Lab fiz 1, fff, dużo
Lab fiz 24 233333, fff, dużo
pierwsza strona sprawozdania, fff, dużo
FIZYKA 47, fff, dużo
Lab fiz 43 2, Studia, Semestr 1, Fizyka, Sprawozdania
Lab fiz 15, Studia, Semestr 1, Fizyka, Sprawozdania
76bmoje, fff, dużo
Indukcyjność cewki, fff, dużo
więcej podobnych podstron