Tomasz Andryszewski

Ćwiczenie 2.

Wyznaczanie stałych równania Tafela

Przepływ prądu stałego przez roztwór elektrolitu może dostarczyć ważnych informacji o samym roztworze elektrolitu a przede wszystkim o procesach elektrodowych. Zanurzając do roztworu HCl dwie obojętne, elektrody platynowe i podłączając je do zewnętrznego źródła prądu stałego można wymusić proces elektrolizy pod warunkiem przyłożenia napięcia nieco wyższego od napięcia
określonego wzorem:

(1)

W równaniu (1) A jest powinowactwem chemicznym reakcji zachodzącej podczas elektrolizy, v_e jest to bezwzględna wartość stechiometrycznego współczynnika elektronów zaś F to stała Faraday'a. W wyniku elektrolizy na katodzie zachodzi proces redukcji zaś na anodzie utleniania.

Najważniejszym etapem procesu elektrodowego jest etap przeniesienia ładunku pomiędzy substratem a elektrodą metaliczną. Właśnie te przeniesienie ładunku jest najwolniejszym etapem procesu elektrodowego. Szybkość procesu elektrodowego v mierzy się za pomocą gęstości prądowej i:

(2)

W równaniu (2) n to liczba elektronów biorąca udział w reakcji elektrodowej. Wprowadzając pojęcie nadpotencjału (nadnapięcia) η, jako różnicy potencjałów elektrody spolaryzowanej i elektrody odwracalnej, co można zapisać jako równanie:

(3)

można zapisać równanie (2) opisujące szybkość procesu elektrodowego w postaci najczęściej spotykanej:

(4)

W równaniu (4) α oznacza współczynnik przejścia,
. Nadpotencjał η wchodzący anodzie skład równania (4) jest zależny jedynie od procesu przenoszenia ładunku i bywa nazywany nadpotencjałem aktywacyjnym. Przyjmuje się ponadto, że dla procesu katodowego η_k<0 oraz i_k>0, procesowi anodowemu będzie odpowiadał η_a>0 oraz i_a<0. Jeżeli η_k<0 to równanie (4) upraszcza się do postaci:

(5)

Logarytmując równanie (5) otrzymujemy postać:

(6)

Przyjmując, że
oraz
można równanie (6) zapisać w prostszej postaci:

(7)

Równanie (7) nazywa się równaniem Tafela dla procesu katodowego. Podobne przekształcenia stosuje się, gdy rozpatruje się proces anodowy gdzie η_a>0. Wówczas końcowa postać równania Tafela wygląda następująco:

(8)

Sporządzając wykres zależności
otrzymuje się linię prostą, dzięki której można wyznaczyć stałe a_k/a i b_k/a z równań (7) i (8).

Otrzymane wyniki

Badanym roztworem była azotan V niklu

Dane do wykresu:

U [V]	I [mA]	U [V]	I [mA]
-0,00	0	-1,00	0,00178
-0,05	0	-1,05	0,002047
-0,10	0	-1,10	0,002581
-0,15	0	-1,15	0,003471
-0,20	0	-1,20	0,004094
-0,25	0	-1,25	0,006942
-0,30	0,000142	-1,30	0,00979
-0,35	0,000142	-1,35	0,012994
-0,40	0,000178	-1,40	0,01691
-0,45	0,000178	-1,45	0,02047
-0,50	0,000267	-1,50	0,023496
-0,55	0,000267	-1,55	0,025988
-0,60	0,000356	-1,60	0,02759
-0,65	0,000409	-1,65	0,029014
-0,70	0,000445	-1,70	0,030616
-0,75	0,000641	-1,75	0,032218
-0,80	0,000712	-1,80	0,033998
-0,85	0,000801	-1,85	0,035956
-0,90	0,000979	-1,90	0,038626
-0,95	0,001424

Na podstawie powyższych danych stworzono wykres zależności I=f(U)

Równanie linii trendy ma postać y = -0,0478x - 0,0509.

Chcąc wyznaczyć potencjał rozkładowy azotany niklu, należy wstawić do tego równania w miejsce y wartość 0 i rozwiązać otrzymane równanie względem x.

Stąd x = -1,06V

Obliczone gęstości prądu (J) są następujące (zakładamy, że powierzchnia elektrody wynosi 10^-4 m²)

η [V]	J [A/m^2]	lnJ	η [V]	J [A/m^2]	lnJ
0,00	0	--------	-1,00	0,0178	-4,02856
-0,05	0	--------	-1,05	0,02047	-3,88879
-0,10	0	--------	-1,10	0,02581	-3,65699
-0,15	0	--------	-1,15	0,03471	-3,36073
-0,20	0	--------	-1,20	0,04984	-2,99894
-0,25	0	--------	-1,25	0,06942	-2,66758
-0,30	0,001424	-6,55429	-1,30	0,0979	-2,32381
-0,35	0,001424	-6,55429	-1,35	0,12994	-2,04068
-0,40	0,00178	-6,33114	-1,40	0,1691	-1,77727
-0,45	0,00178	-6,33114	-1,45	0,2047	-1,58621
-0,50	0,00267	-5,92568	-1,50	0,23496	-1,44834
-0,55	0,00267	-5,92568	-1,55	0,25988	-1,34754
-0,60	0,00356	-5,63799	-1,60	0,2759	-1,28772
-0,65	0,004094	-5,49823	-1,65	0,29014	-1,23739
-0,70	0,00445	-5,41485	-1,70	0,30616	-1,18365
-0,75	0,006408	-5,05021	-1,75	0,32218	-1,13264
-0,80	0,00712	-4,94485	-1,80	0,33998	-1,07887
-0,85	0,00801	-4,82706	-1,85	0,35956	-1,02287
-0,90	0,00979	-4,62639	-1,90	0,38626	-0,95124
-0,95	0,01424	-4,2517

Kolejnym krokiem było stworzenie wykresu zależności

Na podstawie równania linii trendu jestem w stanie wyznaczyć stałe równania Tafela

η_k = -0,2241 ln(J) - 1,8694, stąd stałe mają wartości:

a = -1,8694 V

b = -0,2241 V

Znając wzór opisujący nadpotencjał dla znacznej polaryzacji

wyznaczyć mogę:

1. współczynnik przeniesienia ładunku dla procesu katodowego

, gdzie

- współczynnik przeniesienia ładunku dla procesu katodowego

R - stała gazowa (8,31433 J/mol*K)

Z - ilość wymienianych elektronów przez kation (z = 2)

b - stała równania Tafela

F - stała Faradaya 96500C/mol

T - temperatura (273,15K)

Stąd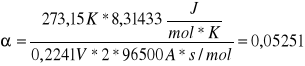

2. gęstość prądu wymiany

Zestawienie otrzymanych wyników:

] Roztwór	Potencjał rozkładowy [V]	Ładunek kationu z	Gęstość prądu wymiany J0 [Am^-2]	Współczynnik przeniesienia ładunku α
Ni(NO3)2	-1,06	2	2,3828*10^-4	0,05251