Marta Złocinska Rzeszów 11.04.03

I SD L-12

ĆWICZENIE 45

Sprawdzanie prawa Malusa. Wyznaczanie

rozkładu światła spolaryzowanego

Zagadnienia do samodzielnego opracowania:

1. Ruch falowy, rodzaje fal.

2. Polaryzacja fali i jej rodzaje.

3. Polaryzacja światła przy odbiciu i załamaniu.

4. Polaryzatory.

5. Wielkości fotometryczne.

Wprowadzenie:

Fale elektromagnetyczne (a więc światło) są falami poprzecznymi. Wektory natężenia pola elektrycznego i magnetycznego fali są prostopadłe do kierunku rozchodzenia się fali. Dla fal elektromagnetycznych można więc także wprowadzić pojęcie polaryzacji fali.

W przypadku fal elektromagnetycznych polaryzacja polega na uporządkowaniu drgań wektora natężenia pola magnetycznego w stosunku do kierunku rozchodzenia się fali. W myśl przejętej umowy polaryzację światła określa kierunek wektora natężenia pola elektrycznego fali E . Płaszczyznę prostopadłą do wektora E przyjęto nazywać płaszczyzną polaryzacji fali. Polaryzacji światła można dokonać przez odbicie i załamanie.

1.Polaryzacja przez odbicie.

Światło naturalne można spolaryzować przez odbicie od powierzchni przezroczystego dielektryka. Jeżeli przez

I_r

R = _

I_o

Oznaczymy zdolność odbijającą ciała, gdzie I_r oznacza natężenie światła odbitego, I_o zaś natężenie światła padającego to według Frensela gdy wektor E leży w płaszczyźnie padania:

I _||r ⋅ tg²()

R_|| = ______ (1)

I _||o ⋅ tg²()

gdy zaś wektor E jest prostopadły do płaszczyzny padania, wówczas:

I _⊥r ⋅ sin²()

R_⊥ = ______ (2)

I _⊥o ⋅ sin²()

Stopień polaryzacji światła odbitego wyraża się następująco:

R_⊥ - R_||

P = ___ (3)

R_⊥ + R_||

Ze wzoru (1) wynika, że gdy tg²() = ∞ , czyli gdy   ° , to R_|| = 0 .

Oznacza to, że światło odbite nie zawiera drgań równoległych do płaszczyzny padania. zatem w przypadku gdy   ° , światło odbite światło odbite jest całkowicie spolaryzowane. Stopień polaryzacji P=1. Kąt padania (Brewestera) _p , przy którym to zachodzi nazywamy kątem polaryzacji.

sin

tg _p = n = ___ prawo Brewestera

sin

Przy użyciu dwóch płytek szklanych można pokazać, że światło po odbiciu od pierwszej płytki pod kątem Brewestera jest całkowicie spolaryzowane. Gdy płaszczyzny padania promieni na pierwszą i na drugą płytkę są do siebie prostopadłe, światło odbite od drugiej płytki znika. Płytka na której zachodzi polaryzacja nazywa się polaryzatorem, a druga analizatorem.

2. Polaryzacja przy podwójnym załamaniu

Przy rozchodzeniu się światła ze źródła punktowego w ośrodku jednorodnym o właściwościach izotropowych czoła fali maja postać sfer współśrodkowych. Istnieje jednak wiele substancji krystalicznych wykazujących właściwości anizotropowe pod względem rozchodzenia się światła. W tych kryształach prędkość rozchodzenia się światła zależy od kierunku i jest inna dla różnych kierunków. Kryształy o takich właściwościach nazywamy kryształami podwójnie łamiącymi. W kryształach podwójnie łamiących rozchodzą się dwa ciągi fal, jednak możemy w nich wyróżnić co najmniej jeden kierunek, dla którego prędkość rozchodzenia się obu ciągów fal jest jednakowa. Kierunek ten jest osią optyczną kryształu.

Promień świetlny przechodzący przez kryształ podwójnie łamiący w kierunku nie pokrywającym się z osią optyczną kryształu zostaje rozszczepiony na dwa promienie, zwyczajny i nadzwyczajny. Promień zwyczajny ma w krysztale we wszystkich kierunkach jednakową prędkość fazową, czyli jednakowy współczynnik załamania. Współczynnik załamania promienia nadzwyczajnego zależy od kierunku rozchodzenia się światła. W kierunku osi optycznej oba współczynniki są jednakowe (brak rozszczepiania) w kierunku prostopadłym do osi optycznej różnica współczynników załamania jest maksymalna. Jeżeli promień zwyczajny rozchodzi się w krysztale szybciej to kryształ taki nazywamy podwójnie łamiącym dodatnim.

Dla usuwania promienia zwyczajnego lub nadzwyczajnego w celu uzyskania jednej wiązki światła spolaryzowanego liniowo używa się pryzmatu Nikola, pryzmatu Wollastone'a albo tez polaroidu.

Układ pomiarowy

Wykonanie ćwiczenia:

Przyrządy :

ława optyczna, źródło światła z polaryzatorem, skala kątowa z analizatorem, układ optyczny detektora, zasilacz i elektroniczny miernik oświetlenia.

Badanie stanu spolaryzowania wiązki światła odbywać się może za pomocą układu składającego się z dwóch ośrodków polaryzujących zwanych polaryzatorem i analizatorem. Po przejściu przez polaryzator światło jest liniowo spolaryzowane. Kolejno, światło przechodząc przez analizator jest ponownie polaryzowane liniowo. Konsekwencją takiego stanu spolaryzowania wiązki świetlnej jest jego zmiana jego natężenia po przejściu przez układ polaryzator - analizator. Zależność tę opisuje prawo Malusa:

I = I _o cos² prawo Malusa

I - natężenie światła opuszczającego analizator

I _o - natężenie światła padającego na analizator

 - kąt zawarty między osiami głównymi polaryzatora i analizatora

Czynności:

1. Włączyć układ pomiarowy.

2. Ustawić analizator (przez przesunięcie skalą kątową) tak aby wskazanie miernika oświetlenia było najmniejsze.

3. Zmieniając kąt ustawienia skali kątowej odczytać kolejne wartości oświetlenia

w luksach.

4. Pomiary przeprowadzić dla pełnego kąta płaskiego (360).

5. Powtórzyć ponownie kilka pomiarów w celu oszacowania błędów.

6. Oszacować błędy dodatkowe (odczyt kąta).

7.Sporządzić wykres zależności natężenia światła I w funkcji kąta w układzie
biegunowym (z uwzględnieniem błędów).

Lp.	α	I	Ispraw.	I	αmax
		[ °]	[lx]	[lx]	[lx]	[ °]
1	0	5,2	5,1	0,1	1
2	15	5,0	4,9	0,1	1
3	30	4,3	4,25	0,05	1
4	45	3,2	3,1	0,1	1
5	60	1,9	1,9	0	1
6	75	0,8	0,8	0	1
7	90	0,35	0,3	0,05	1
8	105	0,6	0,55	0,05	1
9	120	1,5	1,5	0	1
10	135	2,8	2,75	0,05	1
11	150	4,0	3,9	0,1	1
12	165	4,8	4,65	0,15	1
13	180	5,0	5,0	0	1
14	195	4,9	4,85	0,05	1
15	210	4,3	4,2	0,1	1
16	225	3,2	3,1	0,1	1
17	240	2,0	1,9	0,1	1
18	255	0,8	0,85	0,05	1
19	270	0,3	0,35	0,05	1
20	285	0,6	0,55	0,05	1
21	300	1,5	1,5	0	1
22	315	2,8	2,75	0,05	1
23	330	4,0	3,9	0,1	1
24	345	4,8	4,7	0,1	1
25	360	5,2	5,1	0,1	1

Błędy względne pomiaru w procentach:

Przykładowe obliczenia :

= (0,1/5,2)100% 2%

= (0,1/5,0)100% 1%

= (0,05/4,3)100% 1%

Wnioski:

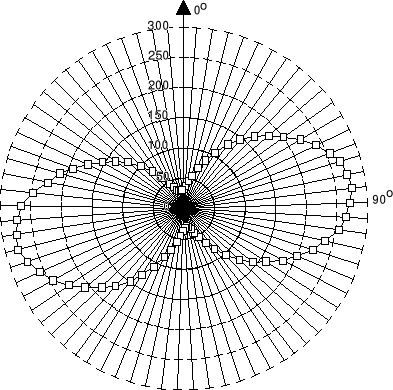
Błędy pomiaru oświetlenia zawierają się w granicach 1 5 % , błąd odczytu kąta 1. Na podstawie wykresu (uwzględniając błędy) możemy stwierdzić, że natężenie światła I jest proporcjonalne do sin2. Prawo Malusa opisuje tę zależność jako zależność cos2. Wynikałoby z tego, że dla = 0 rzeczywiste przesunięcie między osiami polaryzatora i analizatora jest równe 90

Zależność natężenia światła I w funkcji kąta  w układzie biegunowym.

I = f()

4

3

---