POLITECHNIKA ŚLĄSKA

W GLIWICACH

WYDZIAŁ ELEKTRYCZNY

Wyznaczanie energii maksymalnej

promieni metodą absorbcyjną.

WPROWADZENIE

Promieniowanie jądrowe może być wynikiem samorzutnego rozpadu niestabilnych jąder atomowych lub otrzymywane sztucznie podczas przyśpieszania cząstek naładowanych.Rozpad promieniotwórczy jest przemianą jądra w inne jądro o niższym stanie energetycznym , a przemianie towarzyszy emisja cząstek , elektronów ( cząstek ) lub fali elektromagnetycznej ( promienie ) .

W czasie dt nastąpi rozpad :

dN = - N dt

jąder.Całkowanie tego wyrażenia daje prawo rozpadu promieniotwórczego :

gdzie
-liczba początkowa jąder , N - liczba jąder , która pozostała.

Wielkość jest nazywana STAŁĄ ROZPADU i określa prawdopodobieństwo rozpadu jądra w czasie 1 s. Szybkość rozpadu charakteryzuje CZAS POŁOWICZNEGO ZANIKU , po którym liczba jąder preparatu zmniejszy się dwukrotnie :

skąd :

Średni czas życia pojedynczego jądra jest równy odwrotności stałej rozpadu :

Wielkością charakteryzującą preparaty promieniotwórcze jest AKTYWNOŚĆ:

równa liczbie rozpadów w jednostce czasu.Jednostką aktywności źródeł promieniotwórczych jest 1 KIUR ( Ci ) , kiedy to w czasie 1 s zachodzi

3.7*10^10 rozpadów.Inna jednostka aktywności - 1 rutherford odpowiada liczbie zliczeń
Naturalne rozpady promieniotwórcze zachodzą z emisją jednego z trzech rodzajów promieniowania :

1. promieniowania

2. promieniowania :

a) rozpad negatonowy ( z powstaniem antyneutrina )

b) rozpad pozytonowy ( z neutrinem )

c) wychwyt elektronu

3.promieniowania .

Teorię rozpadu opracował E.Fermi .Jak już powiedzieliśmy , rozpad promieniotwórczy może być realizowany na trzy sposoby:

1) emisja elektronów:

2) emisja pozytonów:

3) wychwyt elektronów z powłoki przyjądrowej:

.

Pierwszy z rozpadów może zachodzić dla swobodnego nukleonu , natomiast dwa pozostałe tylko dla nukleonów w jądrach.Energia emitowanych cząstek osiąga wartości od zera do pewnej wartości maksymalnej , a widmo ma charakter ciągły.Energia cząstek może osiągać wartości od 10 keV do 10MeV.Największą energię posiadają cząstki w przypadku , gdy rozpad zachodzi bez udziału neutrino ( bądź antyneutrino ).Dokładne pomiary energii cząstek oparte są na pomiarze odchylenia ich toru w polach magnetycznych w spektrometrach z polem płaskim lub z ogniskowaniem.Elektrony ze względu na mniejszą masę posiadają zwykle mniejszą energię od energii cząstek , i są słabiej pochłaniane przez materię.Niech strumień n cząstek pada na materiał o grubości dx i koncentracji N centrów oddziaływania z tymi cząstkami. Wskutek oddziaływania z wiązki zostanie usuniętych dn cząstek , a liczba ta wyniesie:

Współczynnik nazywa się przekrojem czynnym oddziaływania cząstek z materią i ma wymiar
.Przekrój czynny ma małe wartości i dlatego wprowadzono nową jednostkę: 1 barn (1b)=
.

Elektrony mogą być usuwane z wiązki wskutek:

1) jonizacji ,

2) zderzeń sprężystych z elektronami i jądrami ,

3) zderzeń niesprężystych i związanego z nimi promieniowania hamowania.

Największą wartość osiąga przekrój czynny na jonizację

Proces przejścia elektronów przez absorbującą substancję jest złożony, a zanim energia zmaleje do zera , może zderzyć się z wieloma elektronami (lub jądrami).Jak już wcześniej mówiliśmy w wiązce cząstek mamy elektrony lub pozytony o ciągłym widmie energetycznym.Absorbcję cząstek opisuje funkcja eksponencjalna :

I=Ioe^-x , gdzie

x-grubość absorbenta , -liniowy współczynnik pochłaniania.

OPIS METODY POMIAROWEJ.

Energię maksymalną cząstek możemy wyznaczyć z zależności empirycznych. W naszym przypadku analizujemy proces absorbcji promieni przez folię aluminiową.Przyjmując , że liczba zliczeń przelicznika w określonym czasie proporcjonalna jest do natężenia wiązki promieni wchodzących przez okienko licznika Geigera-M
llera , można zależność przedstawić na wykresie w skali logarytmicznej.Zwiększanie grubości absorbenta nie doprowadzi do uzyskania zerowej liczby zliczeń. Nawet podczas nieobecności źródła promieniotwórczego układ licznik-przelicznik zarejestruje pewną liczbę zliczeń , zwaną TŁEM.Impulsy tła mogą powstać pod wpływem promieniowania kosmicznego , promieniotwórczości zanieczyszczeń powietrza , samorzutnymi wyładowaniami licznika i szumem układu zliczającego.Zasięg liniowy wyznaczamy przedłużając prostoliniowy odcinek wykresu do przecięcia z rzędną odpowiadającą logarytmowi tła.Z wykresu zależności zasięgu masowego promieni w aluminium(dane z tablic) określamy energię maksymalną cząstek stosowanego preparatu.

PRZEBIEG ĆWICZENIA.

Włączamy przelicznik , mierzymy tło licznika (pomiar liczby zliczeń w czasie 10 min.).Preparat promieniotwórczy umieszczamy w domku ołowianym w odległości ok. 1 cm od okienka licznika.

Nastawiamy tryb pomiaru czasu zliczania [s] zadanej liczby impulsów ,np.10^4.

Pomiary wykonujemy najpierw bez absorbenta , a następnie z płytkami aluminiowymi dokładanymi na stos na preparacie.

Pomiary rozpoczynamy od najcieńszych płytek .W miarę zwiększania się czasu można zmniejszyć zadaną liczbę impulsów.

Po dokonaniu pomiarów wykonujemy wykres zależności
= f(d).

Na papierze półlogarytmicznym wykreślamy zależność
.

Określamy zasięg liniowy promieni w aluminium.

Obliczamy zasięg masowy promieni .Na podstawie danych poniższej tablicy rysujemy wykres zasięgu masowego promieni w aluminium od ich energii maksymalnej.

Emax [keV]	100	150	200	250	300	400	500	800	1000
Zm[mg/ ]	13.5	26.5	42	59	78	120	165	310	420

1. Określamy następnie energię maksymalną promieni stosowanego preparatu
Przeprowadzamy graficzną analizę błędów.

TABELA POMIAROWA

TŁO [10min]= 137

LP.	GRUBOŚĆ d [mm]	IMPULSY N	CZAS t[s]	[1/min][0.01%]
1	0	10000	36.92	16251.35162.51
2	0.02		40.11	14958.86149.59
3	0.04		43.75	13714.29137.14
4	0.06		47.35	12671.59116.72
5	0.08		52.40	11450.38114.50
6	0.1		56.22	10672.36106.72
7	0.12		60.28	9953.5599.54
8	0.14		66.90	8968.1089.68
9	0.16		71.92	8342.6083.43
10	0.18		76.93	7799.3077.99
11	0.20		83.87	7153.9371.53
12	0.22		91.13	658465.84
13	0.24		98.69	6079.6460.80
14	0.26		106.20	5649.7256.50
15	0.28		117.01	5127.7751.28
16	0.30		127.47	4706.9947.07
17	0.32		133.27	4502.1445.02
18	0.34		147.98	4054.6040.55
19	0.38		173.60	3456.2234.56
20	0.44		229.55	2615.8625.16
21	0.50		297.37	2017.6920.18
22	0.56		394.55	1520.7215.21
23	0.61	1000	52.3	1147.2311.47
24	0.70	1000	97.4	616.026.16
25	0.79	1000	185.1	324.153.24
26 --> [Author:J]	0.89	1000	228.3	262.812.63

ANALIZA BŁĘDÓW

Wykonując pojedynczy pomiar liczby zliczeń przy pomocy przelicznika można temu pomiarowi przypisać błąd średni równy pierwiastkowi kwadratowemu z liczby zliczeń N:

Błąd bezwzględny oznacza odchylenie wyniku pomiaru od wartości rzeczywistej i podawany jest w jednostkach wielkości mierzonej , w naszym przypadkuX=

= 1). 16251.35162.51 ,pozostałe wartości podane w tabeli pomiarowej.

Błąd względny wyrażony jest stosunkiem błędu bezwzględnego do wielkości mierzonej :

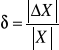
BŁĄD WZGLĘDNY [%]

Przy pomiarach ,gdzie liczba zliczeń jest równa 10000 błąd względny jest równy 1%.

REGRESJA LINIOWA y = ax + b

a = - 1747.062857809772 165.5248079505697

b = 11868.23170564967 394.8016974277826

Współczynnik korelacji r = - 0.90706

Zaokrąglenia :

a =

b =

WNIOSKI

Wykonane ćwiczenie wykazało , że pochłanianie energii promieniowania jest zależne od grubości absorbenta , którym jest w naszym przypadku aluminium .

Po przez zwiększanie grubości absorbenta liczba przenikających cząstek przez absorbent maleje.

Dla cząstek można wyznaczyć tzw zasięg efektywny R ,czyli grubość absorbenta , którą przenika tylko bardzo mała część padających cząstek .

y = ax + b

10000 = -1750x + 11900

x = 1.08

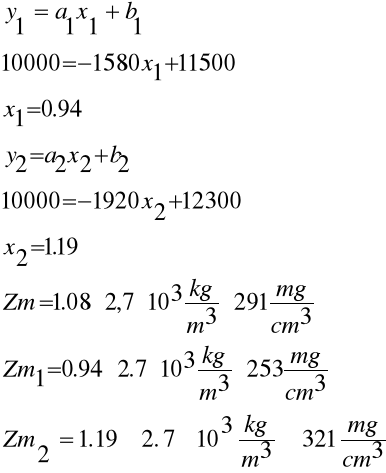
Przedłużenie prostoliniowego odcinka wykresu zależności ln |N'| do przecięcia z rzędną odpowiadającą logarytmowi tła wyznacza zasięg liniowy promieni w aluminium.

Znając zasięg liniowy obliczamy zasięg masowy mnożąc zasięg liniowy przez gęstość materiału.

Gęstość aluminium -

Zasięg liniowy promieni wynosi 1.048mm

Obliczamy zasięg masowy promieni

Zm =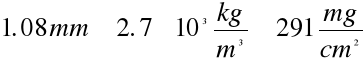
Znając zasięg masowy Zm możemy odczytać energię maksymalną promieni w aluminium

LINEARYZACJA ODCINKOWA

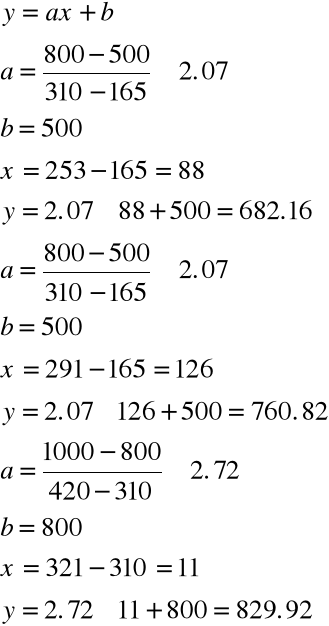
TŁO [10min]=60 N'= 6 [imp/min] ln (N') =1.79

LP.	GRUBOŚĆ d [mm]	CZAS t[s]	N' [1/min]	ln (N')
1	0	60	11497	9.35
2	0.02	60	9856	9.2
3	0.04	60	8910	9.09
4	0.06	60	7832	8.97
5	0.08	60	7213	8.88
6	0.1	60	6579	8.79
7	0.12	60	6040	8.71
8	0.14	60	5471	8.61
9	0.16	60	5059	8.53
10	0.18	60	4675	8.45
11	0.20	60	4239	8.35
12	0.22	60	4104	8.32
13	0.24	60	3711	8.22
14	0.26	60	3488	8.16
15	0.35	60	2269	7.73
16	0.44	60	1336	7.2
17	0.49	60	1054	6.96
18	0.53	60	897	6.8

0.05 i 0.09

0.05 i 0.09

Strona: 7

---