Kolokwium poprawkowe z kinematyki

1. Wiedząc, że
i
oblicz wartość wyrażenia:

.

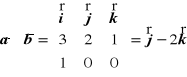
2. Wiedząc, że
i
oblicz wartość wyrażenia
:

Na podstawie tożsamości
obliczamy
,
oraz

.

3. Wiedząc, że
i
oblicz wartość wyrażenia:

.

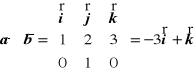
4. Wiedząc, że
i
oblicz wartość wyrażenia
:

Na podstawie tożsamości
obliczamy
,
oraz

.

5. Sformułuj i objaśnij twierdzenie o rozkładzie przyspieszenia punktu na przyśpieszenie normalne i styczne.

Odp.:
gdzie
jest przyspieszeniem stycznym,
jest przyśpieszeniem normalnym,
jest jednostkowym wektorem stycznym,
jest krzywizną toru,
jest promieniem krzywizny toru,
jest jednostkowym wektorem normalnym.

6. Dane są równania ruchu płaskiego punktu materialnego:
gdzie
i 
są stałymi. Wyznaczyć przyspieszenie normalne i styczne w chwili
.

Odp.:
.

7. Dane są równania ruchu płaskiego punktu materialnego:
gdzie
i 
są stałymi. Wyznaczyć przyspieszenie normalne i styczne w chwili
.

Odp.:
.

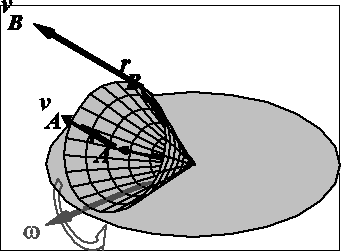
8. Stożek prawidłowy o wysokości h i rozwartości 2 toczy się bez poślizgu po poziomej płaszczyźnie. Wiadomo, że wartość bezwzględna wektora prędkości kątowej stożka jest stała i wynosi
. Oblicz wartość bezwzględną prędkości środka podsyawy stożka / najwyższego punktu podstawy stożka.

Odp.:
/
.

Obliczenia: Z warunkó zadania wynika, że stożek porusza się ruchem kulistym wokół swego wierzchołka a linia kontaktu stożka z płaszczyzną jest osią chwilowego obrotu stożka. Zatem prędkość punktu A obliczmy ze wzoru . Zatem wartość bezwzględna prędkości punktu A wynosi . Dla punktu jest podobnie oraz .

9. Sformułuj i objaśnij twierdzenie o prędkościach i przyśpieszeniach punktów bryły.

Pdp.: Prędkość i przyśpieszenie punktu bryły o położeniu
względem innego punktu A bryły wynoszą odpowiednio

,

gdzie
jest wektorem prędkości kątowej bryły, a
jest wektorem przyśpieszenia kątowego bryły.

10. Wiadomo, że punkty A, B i C o współrzędnych [0,0,0], [1,0,0] i [0,1,0] mają prędkości o składowych odpowiednio [1,1,2], [1,3,1] i [-1,1,3] w tym samym układzie współrzędnych. Wyznaczyć składowe wektora prędkości kątowej bryły.

Odp.:
.

Obliczenia: Korzystamy ze wzorów
i
otrzymując następujący układ równań
=0,
=0.

11. Wiadomo, że punkty A, B i C o współrzędnych [0,0,0], [1,0,0] i [0,1,0] mają prędkości o składowych odpowiednio [1,1,2], [1,3,1] i [-1,1,4] w tym samym układzie współrzędnych. Wyznaczyć składowe wektora prędkości kątowej bryły.

Odp,:
.

Obliczenia: Korzystamy ze wzorów
i
otrzymując następujący układ równań
=0,
=0.

12. Korba o długości r układu korbowego obraca się ze stałą prędkością kątową . Obliczyć wartości przyśpieszeń końca korbowodu w jednym z jego skrajnych położeń. Założyć, że długość korbowodu l>r.

Odp.:
.

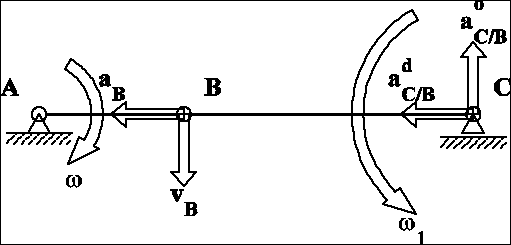
Obliczenia: Z ruchu obrotowego korby wynika
i
. Z więzów korbowodu wynika, że C jest środkiem chwilowego obrotu korbowodu. Ze wzoru
wynika zatem prędkość obrotowa
korby oraz przyśpieszenie
dośrodkowe punktu C względem B. Wobec wzoru
oraz więzów wynika , że przyśpieszenie obrotowe punktu C względem A
. Zatem
oraz
.

13. Sformułuj i objaśnij twierdzenie o prędkościach w ruchu złożonym punktu.

Odp.: Jeżeli równania ruchu punktu materialnego przedstawić w postaci

gdzie
są współrzędnymi rozpatrywanego punktu względem zaczepionego w punkcie
ruchomego układu współrzednych o wersorach

to prędkość bezwzględna punktu wynosi
gdzie

jest prędkością względną, a

jest prędkością unoszenia, natomiast
jest wektorem prędkości kątowej ruchomego układu współrzędnych.

14. Sformułuj i objaśnij twierdzenie o przyśpieszeniach w ruchu złożonym punktu.

Odp.: Jeżeli równania ruchu punktu materialnego przedstawić w postaci

gdzie
są współrzędnymi rozpatrywanego punktu względem zaczepionego w punkcie
ruchomego układu współrzednych o wersorach

to przyspieszenie bezwzględne punktu wynosi
gdzie

jest przyśpieszeniem względnym,

jest przyśpieszeniem unoszenia, a

jest przyspieszeniem Coriolisa natomiast
i
są wektorami prędkości i przyspieszenia kątowego ruchomego układu współrzędnych.

---