Ukryte wymiary - Brian Greene

Dzięki szczególnej i ogólnej teorii względności Einsteinowi udało się rozwikłać dwie zasadnicze sprzeczności naukowe ostatniego stulecia. Kiedy dostrzegł owe problemy, nie przypuszczał, że ich usunięcie zrewolucjonizuje nasze poglądy na przestrzeń i czas. Teoria strun rozwiązuje trzecią z wielkich zagadek ostatniego stulecia. Wymaga jednak, abyśmy poddali nasze wyobrażenia o przestrzeni i czasie tak radykalnej zmianie, że nawet Einsteinowi wydałaaby się ona niezwykła. Teoria strun wstrząsa podstawami współczesnej fizyki. Zdecydowanie i przekonująco odrzuca nawet powszechnie przyjętą liczbę wymiarów Wszechświata - wartość uznawaną dotąd za niepodważalną.

Iluzja znajomości

Doświadczenie kształtuje intuicję. Tworzy także układ odniesienia dla analizowanych i interpretowanych zjawisk. Niewątpliwie spodziewamy się, że na przykład dziecko wychowane przez stado wilków będzie interpretowało świat zupełnie inaczej niż my. Nawet porównywanie ludzi wyrosłych w różnych kulturach uwidacznia przemożny wpływ doświadczeń na nasz sposób myślenia.

Istnieje jednak pewien wspólny zbiór doświadczeń. I to często właśnie przekonania wynikające z powszechnego doświadczenia najtrudniej zidentyfikować i podważyć. Oto prosty, ale istotny przykład. Kiedy skończymy czytać, poruszymy się w trzech niezależnych kierunkach, czyli w trzech niezależnych wymiarach przestrzennych. Każda z wybranych przez nas dróg - nieważne, jak będzie skomplikowana - to kombinacja ruchu w wymiarach prawo-lewo, przód-tył i góra-dół. Zawsze gdy robimy krok, tak naprawdę dokonujemy trzech niezależnych wyborów, które określają nasz sposób przemieszczania się w tych trzech wymiarach.

Przypomnijmy pewne równoważne stwierdzenie przywoływane w rozważaniach na temat szczególnej teorii względności. Otóż każde miejsce we Wszechświecie w pełni się określa, podając trzy informacje, czyli mówiąc, gdzie się ono znajduje względem tych trzech wymiarów przestrzennych. Przykładem zaczerpniętym z codziennego doświadczenia jest podawanie adresu przez mieszkańca miasta. Wymienia on nazwę ulicy (miejsce w "wymiarze prawo-lewo"), nazwę przecznicy lub głównej alei (umiejscowienie w "wymiarze przód-tył") oraz numer piętra (lokalizacja w "wymiarze góra-dół"). Przekonaliśmy się, że dokonania Einsteina zachęcają do myślenia o czasie jako o kolejnym wymiarze ("wymiarze przyszłość-przeszłość"). W sumie mamy więc cztery wymiary (trzy przestrzenne i jeden czasowy). Zdarzenia we Wszechświecie określamy, podając, gdzie i kiedy nastąpiły.

Ta właściwość Wszechświata jest tak podstawowa, logiczna i powszechna, że wydaje się niemożliwa do zakwestionowania. Niemniej w 1919 roku mało znany matematyk polskiego pochodzenia, Theodor Kaluza z Uniwersytetu w Królewcu, miał czelność podważyć to, co oczywiste. Postawił on tezę, że w rzeczywistości Wszechświat ma więcej niż trzy wymiary. Niektóre głupio brzmiące pomysły rzeczywiście są bezsensowne, ale część z nich wstrząsa podstawami fizyki. Chociaż musiało upłynąć dość dużo czasu, zanim koncepcja Kaluzy się upowszechniła, zrewolucjonizowała ona pojmowanie prawa fizycznego. Odkrycie to zadziwia nas do dziś.

Pomysł Kaluzy i poprawki Kleina

Stwierdzenie, że nasz Wszechświat ma więcej niż trzy wymiary przestrzenne, niektórym wyda się niedorzeczne, dziwaczne albo mistyczne. W rzeczywistości jednak koncepcja ta jest całkiem prawdopodobna. Najłatwiej będzie się o tym przekonać, analizując prosty przykład. Zamiast więc zajmować się całym Wszechświatem, ograniczymy nasze rozważania do bardziej znajomego obiektu, jakim jest długi i cienki wąż ogrodowy.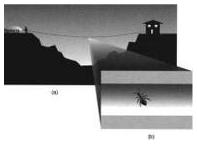


Wyobraźmy sobie, że przeciągamy nad doliną kilkusetmetrowy wąż i patrzymy na niego z odległości, powiedzmy, czterystu metrów, tak jak to pokazano w części (a) ryciny 8.1. Z tej odległości łatwo dostrzeżemy całą rozciągłość węża, ale jeśli nie mamy sokolego wzroku, trudno nam będzie ocenić jego grubość. Gdyby na wężu zamieszkała mrówka, to z naszej odległej perspektywy stwierdzilibyśmy, że porusza się ona tylko w jednym wymiarze - wymiarze prawo-lewo, wzdłuż długości węża. Jeśli ktoś poprosiłby nas o określenie, gdzie znajduje się mrówka w danej chwili, podalibyśmy tylko odległość owada od lewego (lub prawego) końca węża. Z odległości czterystu metrów długi kawałek ogrodowego węża wygląda więc jak obiekt jednowymiarowy.

W rzeczywistości wiemy, że wąż ma pewną grubość. Być może trudno to zobaczyć z odległości czterystu metrów, ale używając lornetki, przyjrzymy się wężowi w powiększeniu i dostrzeżemy jego obwód, jak pokazuje rycina 8.1b. Dzięki powiększeniu zobaczymy, że mrówka żyjąca na wężu ma w rzeczywistości do wyboru dwa niezależne kierunki poruszania się: wzdłuż wspomnianego już wymiaru prawo-lewo, odpowiadającego długości węża, oraz wzdłuż wymiaru "zgodnie z ruchem wskazówek zegara lub przeciwnie do niego", po obwodzie węża. Widzimy teraz, że aby zlokalizować mrówkę, musimy podać dwie informacje: miejsce wzdłuż węża i na jego obwodzie. Powierzchnia węża ogrodowego jest bowiem dwuwymiarowa.

Te dwa wymiary różnią się jednak znacząco. Kierunek wzdłuż węża jest dobrze widoczny ze względu na długość i rozciągłość węża. Kierunek po obwodzie pozostaje "zwinięty". Trudniej go zauważyć, ponieważ wąż jest cienki. Aby dostrzec wymiar związany z obwodem, musieliśmy przyjrzeć się wężowi dużo dokładniej.

Przykład ten uwidacznia istotną właściwość wymiarów przestrzennych. Występują one w dwóch odmianach. Bywają duże, rozciągłe, a więc i dobrze widoczne, albo małe i zwinięte, a te znacznie trudniej wykryć. Oczywiście, nie trzeba się zbytnio wysilać, aby odkryć zwinięty wymiar wzdłuż obwodu węża. Wystarczy spojrzeć przez lornetkę. Gdybyśmy jednak dysponowali bardzo cienkim wężem ogrodowym - tak cienkim jak włos lub naczynko włosowate - dostrzeżenie jego zwiniętego wymiaru okazałoby się trudniejsze.

W artykule przesłanym Einsteinowi w 1919 roku Kaluza przedstawił zdumiewającą propozycję. Zasugerował, że przestrzenna struktura Wszechświata ma więcej niż trzy wymiary znane z codziennego doświadczenia. Kaluza zaproponował tak radykalną zmianę, odkrywszy, że wprowadzenie jej umożliwia stworzenie eleganckiej i przekonującej struktury pojęciowej łączącej ogólną teorię względności Einsteina z teorią elektromagnetyzmu Maxwella. Natychmiast nasuwa się jednak pytanie, jak pogodzić propozycję Kaluzy z tym, że widzimy dokładnie trzy wymiary.

Odpowiedź zawarta była implicite w pracy Kaluzy, a jej poprawioną wersję przedstawił w 1926 roku szwedzki matematyk Oskar Klein. Brzmi ona następująco: struktura przestrzenna naszego Wszechświata ma prawdopodobnie zarówno rozciągłe, jak i zwinięte wymiary. Oznacza to, że Wszechświat przypomina pod tym względem wąż ogrodowy. Ma bowiem wymiary duże, rozciągłe i łatwo dostrzegalne (trzy wymiary przestrzenne znane z codziennego doświadczenia) oraz dodatkowe wymiary przestrzenne (odpowiednik grubości węża), ciasno zwinięte w tak małej przestrzeni, że do tej pory nie udało się ich wykryć za pomocą najlepszej aparatury.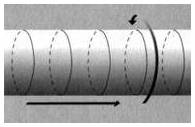


Aby lepiej zrozumieć tę niezwykłą hipotezę, wróćmy do przykładu węża ogrodowego. Wyobraźmy sobie, że wzdłuż obwodu węża, w niedużych odległościach od siebie namalowano czarne okręgi. Jak poprzednio, z daleka wąż wydaje się cienką, jednowymiarową linią. Gdy jednak przyjrzymy mu się przez lornetkę, wykryjemy zwinięty wymiar. Zauważenie go ułatwią namalowane okręgi. Naszym oczom ukaże się taki obraz jak na rycinie 8.2. Pokazuje ona, że wąż ogrodowy ma dwuwymiarową powierzchnię, przy czym jeden z wymiarów jest długi i rozciągły, a drugi - mały i zwinięty. Kaluza i Klein wyrazili przypuszczenie, że nasz przestrzenny Wszechświat wygląda podobnie, z tym że ma nie jeden, a trzy duże, rozciągłe wymiary i jeden mały, zwinięty - co w sumie daje cztery wymiary przestrzenne. Trudno narysować wycinek przestrzeni o takiej liczbie wymiarów, więc dla celów ilustracyjnych ograniczymy się do dwóch dużych wymiarów i jednego małego, zwiniętego. Sytuację taką przedstawia rycina 8.3, na której powiększono strukturę przestrzenną w podobny sposób, jak powiększano powierzchnię węża ogrodowego.


Najniższy poziom na rysunku przedstawia strukturę przestrzeni - zwykły otaczający nas świat - widzianą z odległości kilku metrów. Skalę odległości przedstawiono za pomocą płaszczyzny z podziałką. Na kolejnych poziomach obserwujemy strukturę coraz mniejszych obszarów przestrzeni, które kolejno powiększamy, aby były lepiej widoczne. Na początku, gdy zmniejszamy skalę odległości (pierwsze trzy poziomy powiększenia), nic szczególnego się nie dzieje. Wygląda na to, że struktura przestrzeni zachowuje zasadniczo taką samą postać jak w większych skalach. Gdy jednak dochodzimy do najbardziej mikroskopowych skal - widocznych na czwartym poziomie - dostrzegamy nowy, zwinięty, kołowy wymiar przestrzeni, przypominający pętle nitki w gęsto utkanym dywanie. Kaluza i Klein sugerowali, że kołowy wymiar istnieje w każdym punkcie rozciągłych wymiarów, podobnie jak kołowy obwód ogrodowego węża jest w każdym punkcie wzdłuż jego prostego, poziomego wymiaru. (Aby obrazek był czytelny, narysowaliśmy tylko próbkę kołowego wymiaru w równo oddalonych od siebie punktach rozciągłych wymiarów). Wyobrażenie Kaluzy-Kleina na temat mikroskopowej struktury przestrzennej przedstawia w powiększeniu rycina 8.4.

 

 

Podobieństwo do węża ogrodowego jest wyraźne, chociaż istnieją też spore różnice. Wszechświat ma trzy duże, rozciągłe wymiary przestrzenne (narysowaliśmy tylko dwa z nich), natomiast wąż - jeden i, co ważniejsze, opisujemy przestrzenną strukturę samego Wszechświata, a nie jakiegoś przedmiotu, takiego jak wąż ogrodowy, który znajduje się wewnątrz Wszechświata. Zasadnicza myśl pozostaje jednak identyczna. Podobnie jak w przypadku grubości węża, jeśli dodatkowy, zwinięty, kołowy wymiar Wszechświata jest niezwykle mały, dużo trudniej go wykryć niż dobrze widoczne, duże, rozciągłe wymiary. W rzeczywistości, jeśli ma on odpowiednio mały rozmiar, nie zarejestrujemy go nawet za pomocą najczulszych urządzeń. Co ważniejsze, kołowy wymiar to nie tylko okrągły garb na znanych rozciągłych wymiarach, na co być może wskazuje rycina. Jest on nowym wymiarem, znajdującym się w każdym punkcie rozciągłych wymiarów, podobnie jak we wszystkich punktach istnieje każdy z wymiarów góra-dół, prawo-lewo czy przód-tył. Również w tym kierunku poruszałaby się mrówka, gdyby miała odpowiednio małe rozmiary. Aby wyznaczyć położenie w przestrzeni takiej mikroskopijnej mrówki, musielibyśmy określić jej lokalizację w trzech znanych rozciągłych wymiarach (które pokazuje podziałka), a także w wymiarze kołowym. Potrzebowalibyśmy więc czterech informacji odnośnie do przestrzeni i jednej dotyczącej czasu, czyli w sumie pięciu informacji - o jedną więcej niż zwykle.

Chociaż więc uświadamiamy sobie istnienie tylko trzech rozciągłych wymiarów przestrzennych, zgodnie z rozumowaniem Kaluzy i Kleina nie dowodzi to jeszcze, że nie ma dodatkowych, zwiniętych, bardzo małych wymiarów. Jest całkiem prawdopodobne, że Wszechświat charakteryzuje się większą liczbą wymiarów niż widać.

Jak małe muszą być te dodatkowe wymiary? Najnowocześniejsze urządzenia wykrywają struktury o rozmiarach zaledwie jednej miliardowej miliardowej metra. Jeśli dodatkowy wymiar jest zwinięty do mniejszych rozmiarów, nie damy rady go wykryć. W 1926 roku Klein dodał do pierwotnej koncepcji Kaluzy pewne pomysły z dziedziny rodzącej się mechaniki kwantowej. Z przeprowadzonych przez niego obliczeń wynikało, że dodatkowy kołowy wymiar może być nawet tak mały, jak długość Plancka, a więc znacznie mniejszy niż skale dostępne doświadczalnie. Od tego czasu fizycy określają możliwość istnienia dodatkowych wymiarów przestrzennych mianem teorii Kaluzy-Kleina.

 

Krzątanina na wężu ogrodowym

Przykład z wężem ogrodowym i rycina 8.3 miały nam pomóc w zrozumieniu, jak to możliwe, aby na Wszechświat składały się dodatkowe wymiary przestrzenne. Ale nawet badaczom, którzy zajmują się tą dziedziną, trudno sobie wyobrazić Wszechświat mający więcej niż trzy wymiary przestrzenne. Dlatego fizycy, starając się intuicyjnie pojąć, czym są te dodatkowe wymiary, wyobrażają sobie życie we wszechświecie o mniejszej liczbie wymiarów - podobnym do tego z Krainy Płaszczaków Edwina Abbotta, wspaniałej, klasycznej już książki popularnonaukowej napisanej w 1884 roku. Dzięki temu dostrzegają, iż Wszechświat ma więcej wymiarów, niż widzimy. Pójdźmy za przykładem uczonych i wyobraźmy sobie, że nasz dwuwymiarowy wszechświat ma kształt węża ogrodowego. Musimy zapomnieć o punkcie widzenia zewnętrznego obserwatora. Trzeba porzucić znany nam świat i wejść w nowy wszechświat węża ogrodowego. Powierzchnia węża (powiedzmy, że jest on nieskończenie długi) to wszystko, co istnieje, jeśli chodzi o przestrzenną rozciągłość, a my jesteśmy małą mrówką żyjącą na tej powierzchni.

Na początek zróbmy coś jeszcze bardziej niezwykłego. Wyobraźmy sobie, że kołowy wymiar wszechświata węża ogrodowego ma tak małą długość, że nikt z mieszkańców węża nie zdaje sobie sprawy z jego istnienia. Wszyscy jednogłośnie twierdzą, że wszechświat ten jest jednowymiarowy. (Gdyby w tym wszechświecie narodziła się mrówka Einstein, tubylcy mówiliby, że ich wszechświat ma jeden wymiar przestrzenny i jeden czasowy). Fakt ten wydaje się mieszkańcom węża tak niezaprzeczalny, że postanawiają nazwać swój dom Krainą Liniowców, podkreślając w ten sposób jego jednowymiarowość.

Życie w Krainie Liniowców bardzo się różni od wiedzionej przez nas egzystencji. W krainie tej nie zmieściłoby się na przykład ciało w postaci znanej nam wszystkim. Choćbyśmy włożyli wiele wysiłku w modelowanie sylwetki, z pewnością nie zmienilibyśmy tego, że nasze ciało ma długość i dwie szerokości - rozciągłość w trzech wymiarach. W Krainie Liniowców nie istnieją tak wyszukane formy. Pamiętajmy, że chociaż nasze wyobrażenie Krainy Liniowców nadal może przypominać długi, nitkowaty obiekt umiejscowiony w znanej nam przestrzeni, powinniśmy traktować tę krainę jako cały wszechświat - wszystko, co istnieje. Jako mieszkańcy tego wszechświata musimy mieścić się w jego przestrzennych rozmiarach. Spróbujmy to sobie wyobrazić. Nawet jeśli zmienilibyśmy się w mrówkę, nadal nie byłoby dla nas miejsca w Krainie Liniowców. Musielibyśmy tak ścisnąć swoje mrówcze ciało, aby przekształcić się w miniaturową dżdżownicę. Następnie trzeba by stracić grubość. Chcąc zmieścić się w Krainie Liniowców, musimy ograniczyć swoje wymiary do długości.

Wyobraźmy sobie teraz, że na każdym końcu naszego ciała znajduje się oko. W przeciwieństwie do ludzkiego oka, które obraca się i patrzy we wszystkich trzech kierunkach, oczy Liniowca pozostają nieruchome. Każde z nich spogląda tylko w jednym kierunku. To ograniczenie naszego nowego ciała nie wynika z anatomii. Wszyscy Liniowcy uświadamiają sobie, że skoro Kraina Liniowców ma tylko jeden wymiar, nie istnieje po prostu inny kierunek, w którym można by patrzeć. Przód i tył to jedyne kierunki istniejące w tej krainie.

Gdy rozmyślamy o życiu w Krainie Liniowców, dochodzimy do wniosku, że nic ciekawego nas tam nie czeka. Wyobraźmy sobie na przykład, że przed lub za nami znajduje się inny Liniowiec. Widzimy jedno z jego oczu - to skierowane ku nam - ale oko Liniowca w przeciwieństwie do ludzkiego narządu wzroku jest pojedynczym punktem. Oczy mieszkańców Krainy Liniowców niczym się nie odznaczają, nie wyrażają żadnych uczuć - nie ma po prostu na to miejsca. Co więcej, na zawsze pozostaniemy z tym punktowym obrazem oka naszego sąsiada. Gdybyśmy chcieli minąć Liniowca i zbadać krainę z jego drugiej strony, spotkałoby nas wielkie rozczarowanie. Liniowca nie da się wyminąć. Całkowicie blokuje on przejście. Nie ma miejsca, aby go obejść. Od chwili gdy Liniowcy zostaną rozrzuceni wzdłuż swojej krainy, ich uporządkowanie się nie zmienia. Okropność.

Kilka tysięcy lat po religijnym objawieniu w Krainie Liniowców Liniowiec o nazwisku Kaluza K. Line (od ang.: line - linia) oznajmia zniechęconym mieszkańcom krainy dobrą nowinę. Czy to pod wpływem boskiego natchnienia, czy też na skutek wyczerpania spowodowanego tym, że latami wpatrywał się w oko sąsiada, stawia on hipotezę, że tak naprawdę Kraina Liniowców wcale nie musi być jednowymiarowa. Co by się stało, spekuluje Kaluza, gdyby kraina miała w rzeczywistości dwa wymiary, przy czym drugi z nich byłby bardzo mały i kołowy, i jak na razie nieznany ze względu na swoje niewielkie rozmiary przestrzenne. Przed oczami Liniowców staje obraz całkiem nowego życia. Zaczęliby je wieść, gdyby tylko ten zwinięty wymiar przestrzenny udało się powiększyć, co - zgodnie z najnowszymi odkryciami jego kolegi Linesteina - jest możliwe. Wszechświat opisywany przez Kaluzę wprawia wszystkich mieszkańców krainy w zachwyt i budzi w nich nadzieję. We wszechświecie tym Liniowcy swobodnie przemieszczaliby się obok siebie, wykorzystując drugi wymiar. Koniec z przestrzennym niewolnictwem. Nietrudno się zorientować, że Kaluza K. Line odmalowuje życie w "pogrubionym" wszechświecie węża ogrodowego.

Gdyby kołowy wymiar się zwiększył, rozciągając Krainę Liniowców do postaci wszechświata węża ogrodowego, nasze życie, życie mieszkańców tego świata, rzeczywiście uległoby głębokim zmianom. Przyjrzyjmy się na przykład naszemu ciału. Wszystko, co znajduje się między dwojgiem oczu Liniowców, stanowi wnętrze organizmu. Oczy Liniowca odgrywają więc tę samą rolę co skóra w ciele ludzkim, tworzą barierę oddzielającą go od świata zewnętrznego. Lekarz pracujący w tej krainie dociera do organów wewnętrznych swoich pacjentów tylko po przebiciu powierzchni ciała. Innymi słowy, zabiegi chirurgiczne przeprowadza się przez oczy.


Wyobraźmy sobie teraz, co by się stało, gdyby Kraina Liniowców, zgodnie z twierdzeniami Kaluzy K. Line'a, miała tajemniczy, zwinięty wymiar i gdyby ten wymiar urósł do zauważalnych rozmiarów. Inny Liniowiec widziałby nasze ciało pod kątem, miałby więc możliwość zaglądania do jego wnętrza (por. ryc. 8.5). Dzięki istnieniu tego drugiego wymiaru lekarz przeprowadzałby operację, sięgając bezpośrednio do odsłoniętego wnętrza ciała. To niesamowite! Z czasem Liniowcy z pewnością wytworzyliby osłonkę podobną do skóry, aby odgrodzić się od świata zewnętrznego. Co więcej, niewątpliwie w wyniku ewolucji ciała Liniowców zyskałyby szerokość. Liniowcy przybraliby postać Płaszczaków ślizgających się po dwuwymiarowym wszechświecie węża ogrodowego (por. ryc. 8.6). Gdyby kołowy wymiar znacznie się zwiększył, ten dwuwymiarowy wszechświat przypominałby Krainę P
łaszczaków Abbotta - fikcyjny dwuwymiarowy świat, który Abbott obdarzył bogatą kulturą, nawet ukazanym prześmiewczo systemem kastowym, uzależniającym pozycję społeczną od kształtu geometrycznego. Podczas gdy trudno sobie wyobrazić, aby w Krainie Liniowców nastąpiły jakiekolwiek interesujące zdarzenia - nie starczyłoby po prostu na nie miejsca - życie na wężu ogrodowym oferuje wiele możliwości. Przejście od jednego do dwóch dużych, widocznych wymiarów przestrzennych wiąże się z ogromnymi zmianami.

Dlaczego jednak mielibyśmy na tym poprzestać? Być może w dwuwymiarowym wszechświecie również istnieje zwinięty wymiar. Wówczas wszechświat ten miałby trzy wymiary. Sytuację taką przedstawia rycina 8.4 z zastrzeżeniem, że ukazuje ona teraz świat o dwóch rozciągłych wymiarach przestrzennych (gdy po raz pierwszy odwoływaliśmy się do tej ryciny, płaska siatka miała przedstawiać trzy rozciągłe wymiary). Gdyby wymiar kołowy się rozciągnął, dwuwymiarowa istota zaczęłaby żyć w zupełnie nowym świecie, w którym ruch nie ogranicza się do kierunków prawo-lewo i przód-tył wzdłuż rozciągłych wymiarów. Teraz mieszkaniec tego świata poruszałby się także w trzecim wymiarze - w kierunku góra- -dół wzdłuż okręgu. Gdyby wymiar kołowy osiągnął odpowiednią wielkość, powstałby nasz trójwymiarowy Wszechświat. Obecnie nie wiemy, czy którykolwiek z naszych trzech wymiarów przestrzennych rozciąga się w nieskończoność, czy też się zwija, zataczając olbrzymie koło w odległościach niedostępnych dla naszych najlepszych teleskopów. Gdyby wymiar kołowy z ryciny 8.4 zwiększył się odpowiednio - osiągnął rozmiary miliardów lat świetlnych - rysunek ten byłby obrazem naszego świata.

Powtórzmy jednak raz jeszcze: dlaczego mielibyśmy na tym poprzestać? I tak dochodzimy do hipotezy Kaluzy i Kleina, że nasz trójwymiarowy Wszechświat ma niewidoczny zwinięty czwarty wymiar przestrzenny. Jeśli ta zadziwiająca hipoteza o istnieniu dodatkowego wymiaru (a może istnieje wiele takich wymiarów?) jest prawdziwa, to gdyby ów zwinięty wymiar miał urosnąć do rozmiarów makroskopowych, życie, jakie znamy, zaczęłoby wyglądać zupełnie inaczej.

Co ciekawe, nawet jeśli dodatkowe wymiary na zawsze pozostałyby zwinięte i małe, z samego ich istnienia wynikałyby istotne konsekwencje.

Unifikacja w wyższych wymiarach

Wysunięta przez Kaluzę w 1919 roku hipoteza o istnieniu w naszym Wszechświecie dodatkowych wymiarów przestrzennych sama w sobie zasługiwała na uwagę. Szczególne znaczenie zyskała jednak w związku z ogólną teorią względności Einsteina. Teoria ta odnosiła się do Wszechświata o trzech wymiarach przestrzennych i jednym czasowym. Ale jej matematyczną strukturę dało się w dość prosty sposób rozszerzyć, aby zapisać analogiczne równania dla wszechświata o większej liczbie wymiarów przestrzennych. Przy założeniu, że istnieje tylko jeden dodatkowy wymiar, Kaluza przeprowadził odpowiednią matematyczną analizę i otrzymał nowe równania.

Zauważył, że jego równania odnoszące się do trzech zwykłych wymiarów mają w zasadzie identyczną postać jak równania Einsteina. Ponieważ jednak Kaluza dodał jeden wymiar przestrzenny, zgodnie z oczekiwaniami otrzymał też dodatkowe równania, których teoria Einsteina nie zawierała. Po ich zbadaniu uczony uświadomił sobie coś zadziwiającego. Te dodatkowe równania nie były niczym innym, jak równaniami zapisanymi przez Maxwella w latach osiemdziesiątych XIX wieku, równaniami opisującymi siłę elektromagnetyczną. Dodając jeden wymiar przestrzenny, Kaluza zjednoczył teorię grawitacji Einsteina z teorią światła Maxwella.

Przed odkryciem Kaluzy grawitację i elektromagnetyzm uważano za dwie nie związane ze sobą siły. Mając dość twórczej odwagi, aby wyobrazić sobie, że nasz Wszechświat ma dodatkowy wymiar przestrzenny, Kaluza pokazał, iż tak naprawdę między owymi siłami istnieje ścisła zależność. Zgodnie z jego teorią zarówno grawitacja, jak i elektromagnetyzm wiążą się ze zniekształceniami w strukturze przestrzeni. Grawitację przenoszą zaburzenia w znanych nam trzech wymiarach przestrzennych, natomiast elektromagnetyzm propaguje się dzięki zniekształceniom w nowym, zwiniętym wymiarze.

Kaluza przesłał swój artykuł Einsteinowi, którego początkowo zaintrygowało to odkrycie. 21 kwietnia 1919 roku odpisał Kaluzie, że nigdy nie wpadł na pomysł, aby osiągnąć unifikację przez wprowadzenie "pięciowymiarowego [cztery wymiary przestrzenne i jeden czasowy], cylindrycznego świata". Po czym dodał: "na pierwszy rzut oka Pański pomysł niezmiernie mi się podoba". Tydzień później Einstein wysłał jednak do Kaluzy list wyrażający sceptycyzm: "Przeczytałem dokładnie Pański artykuł i stwierdzam, że jest naprawdę interesujący. Na razie nie znalazłem w nim nic niemożliwego. Z drugiej strony, muszę przyznać, że przytoczone argumenty nie są dość przekonujące". Ponad dwa lata później, po dokładnym przeanalizowaniu nowatorskiego podejścia Kaluzy, 14 października 1921 roku Einstein jeszcze raz do niego napisał: "Zastanawiam się ponownie, czy słusznie zniechęciłem Pana dwa lata temu do publikacji Pańskiego artykułu, zawierającego pomysł na połączenie grawitacji z elektrycznością. [...] Jeśli Pan sobie życzy, ostatecznie jestem skłonny przedstawić Pańską pracę Akademii". W końcu, z opóźnieniem, Kaluza otrzymał aprobatę mistrza.

Chociaż koncepcja Kaluzy była piękna, późniejsze jej badania pokazały, że pozostaje ona w sprzeczności z rezultatami doświadczeń. W wyniku najprostszych prób włączenia do tej teorii elektronu między jego masą a ładunkiem powstawały związki, które znacznie się różniły od zmierzonych wartości. Ponieważ nie znaleziono żadnego sposobu, aby rozwiązać ten problem, fizycy przestali interesować się pomysłem Kaluzy. Einstein i inni co jakiś czas wracali do możliwości istnienia dodatkowych, zwiniętych wymiarów, ale wkrótce tego rodzaju badania znalazły się na peryferiach fizyki teoretycznej.

W rzeczywistości koncepcja Kaluzy znacznie wyprzedzała swoje czasy. Dopiero w latach dwudziestych fizycy teoretyczni i doświadczalni rozwinęli badania, których celem było zrozumienie zasadniczych praw mikroświata. Teoretycy poświęcili się próbom stworzenia mechaniki kwantowej i kwantowej teorii pola. Fizycy doświadczalni musieli jeszcze odkryć szczegółowe właściwości atomu i innych elementarnych składników materii. Teoria kierowała eksperymentem, a eksperyment udoskonalał teorię. Fizycy przez pół wieku parli do przodu, aby w końcu stworzyć Model Standardowy. Nie ma nic dziwnego w tym, że w owych produktywnych i ekscytujących czasach nikt nie zajmował się spekulacjami na temat dodatkowych wymiarów. Kiedy fizycy badali możliwości metod mechaniki kwantowej, a ich przewidywania dawało się doświadczalnie sprawdzić, nie budziła szczególnego zainteresowania hipoteza, że Wszechświat jest zupełnie inny w skalach o wiele mniejszych niż te, które badano za pomocą najlepszych urządzeń.

Ale wcześniej czy później każdy kierunek badań, choćby należał do najbardziej popularnych, przestaje się rozwijać. Teoretyczną strukturę Modelu Standardowego dobrze poznano właściwie do końca lat sześćdziesiątych. Przed początkiem lat osiemdziesiątych wiele przewidywań związanych z tym modelem potwierdzono doświadczalnie i większość fizyków cząstek uznała, że sprawdzenie reszty to tylko kwestia czasu. Chociaż kilka istotnych szczegółów pozostało nie wyjaśnionych, wiele osób czuło, że na zasadnicze pytania dotyczące oddziaływań silnych, słabych i elektromagnetycznych znaleziono już odpowiedź.

W końcu sytuacja dojrzała do tego, aby znów podjąć najważniejszą kwestię związaną z tajemniczą sprzecznością między mechaniką kwantową a ogólną teorią względności. Sukces w sformułowaniu teorii kwantowej opisującej trzy spośród czterech oddziaływań zachęcił fizyków do podjęcia prób włączenia czwartej siły - grawitacji. Przeanalizowano wiele pomysłów. Bezskutecznie. Fizycy stali się wówczas bardziej otwarci na stosunkowo radykalne propozycje. I tak teoria Kaluzy-Kleina, którą odrzucono pod koniec lat dwudziestych, została wskrzeszona.

Współczesna teoria Kaluzy-Kleina

Od momentu wysunięcia przez Kaluzę jego hipotezy minęło sześćdziesiąt lat. Przez ten czas zrozumiano wiele problemów fizycznych. Stworzono i potwierdzono doświadczalnie całą mechanikę kwantową. Odkryto i dobrze poznano oddziaływania silne oraz słabe, nieznane jeszcze w latach dwudziestych. Niektórzy fizycy sugerowali, że pierwotna propozycja Kaluzy nie zdała egzaminu, ponieważ badacz nie wiedział o istnieniu tych sił i w związku z tym jego reforma przestrzeni musiała być konserwatywna. Istnienie większej liczby oddziaływań wiązało się z koniecznością wprowadzenia jeszcze większej liczby wymiarów. Dowodzono, że choć pojedynczy wymiar kołowy wskazuje na istnienie związku między ogólną teorią względności a elektromagnetyzmem, związek ten okazuje się niewystarczający.


Do połowy lat siedemdziesiątych intensywnie badano teorie wskazujące na większą liczbę wymiarów. Rycina 8.7 to przykład przestrzeni z dwoma dodatkowymi zwiniętymi wymiarami. Mają one postać powierzchni piłki, czyli sfery. Tak jak w przypadku pojedynczego wymiaru kołowego, te dodatkowe wymiary dołączone są w każdym punkcie zwykłych rozciągłych wymiarów. (Chcąc zachować przejrzystość rysunku, przedstawiliśmy tylko próbkę sferycznych wymiarów w równo oddalonych od siebie punktach siatki wymiarów rozciągłych). Poszczególne teorie różnią się nie tylko liczbą dodatkowych wymiarów, ale także ich kształtem. Na rycinie 8.8
pokazano fragment przestrzeni o dwóch dodatkowych wymiarach mających kształt obwarzanka, czyli torusa. Łatwo sobie wyobrazić bardziej skomplikowane możliwości, w których różne niesamowite kształty tworzą trzy, cztery, pięć dodatkowych wymiarów przestrzennych, a w zasadzie dowolną ich liczbę. Jedyne ograniczenie wiąże się z tym, że wszystkie wymiary muszą być mniejsze od najmniejszych odległości, jakie potrafimy badać. Żaden eksperyment bowiem nie wykazał jeszcze ich istnienia.

Najbardziej obiecująco zapowiadały się te hipotezy na temat istnienia większej liczby wymiarów, które uwzględniały supersymetrię. Fizycy mieli nadzieję, że częściowe znoszenie się największych fluktuacji kwantowych w wyniku istnienia superpartnerów zwykłych cząstek złagodzi sprzeczność między grawitacją a mechaniką kwantową. Teorie obejmujące grawitację, dodatkowe wymiary i supersymetrię zaczęto nazywać supergrawitacją o wyższej liczbie wymiarów.

Podobnie jak pierwotna hipoteza Kaluzy, różne wersje supergrawitacji wydawały się na początku dość obiecujące. Nowe równania otrzymywane dzięki wprowadzeniu dodatkowych wymiarów niezmiernie przypominały równania używane do opisu elektromagnetyzmu, a także oddziaływań silnych i słabych. Dokładne badania ujawniły jednak, że stare przeszkody pozostały. Co ważniejsze, wprawdzie supersymetria nieco osłabiła zgubne kwantowe zafalowania przestrzeni na małych odległościach, ale nie na tyle, by dało się stworzyć sensowną teorię. Trudno było również znaleźć spójną teorię zakładającą istnienie większej liczby wymiarów, która opisywałaby wszystkie właściwości sił i materii.

Zrozumiano, że choć istnieją fragmenty zunifikowanej teorii, brakuje kluczowego elementu, który połączyłby je ze sobą w sposób kwantowomechanicznie spójny. Ów brakujący element - teoria strun - pojawił się w 1984 roku.

Dodatkowe wymiary i teoria strun

Z tego, o czym pisano wyżej, wynika, iż nie można wykluczyć, że nasz Wszechświat ma dodatkowe zwinięte wymiary przestrzenne o bardzo małych rozmiarach. Dodatkowe wymiary mogą wydawać się nam czymś sztucznym. Niemożność badania odległości mniejszych niż jedna miliardowa miliardowej metra pozwala nam nie tylko wprowadzić w tych skalach dodatkowe wymiary, ale i zrealizować wszelkie najdziwaczniejsze pomysły - nawet umieścić tam mikroskopijną cywilizację z maleńkimi zielonymi ludzikami. Chociaż pierwsza z tych możliwości ma z pewnością bardziej racjonalne uzasadnienie niż druga, postulowanie każdej z tych niezbadanych doświadczalnie - i obecnie niemożliwych do sprawdzenia - ewentualności wydaje się równie uprawnione.

Tak było przed powstaniem teorii strun. Struktura ta rozwiązuje zasadniczą sprzeczność współczesnej fizyki - niezgodność między mechaniką kwantową a ogólną teorią względności - i daje zunifikowany obraz wszystkich podstawowych składników materii i sił natury. Okazuje się jednak, że dokonuje tego, zakładając istnienie we Wszechświecie dodatkowych wymiarów przestrzennych.

Oto dlaczego. Do największych osiągnięć mechaniki kwantowej należy konstatacja, że nasza możliwość przewidywania zasadniczo ogranicza się do stwierdzeń, iż dany wynik otrzymamy z określonym prawdopodobieństwem. Chociaż można się zgodzić z opinią Einsteina, iż jest to niepożądana cecha naszego obecnego obrazu natury, wydaje się, że tak wygląda rzeczywistość. Przyjmijmy ją więc. Wszyscy wiemy, że prawdopodobieństwa określa się za pomocą liczb o wartościach między 0 a 1 lub procentowo - wtedy liczby mają wartości od 0 do 100. Fizycy stwierdzili, że podstawową oznaką zawodności teorii kwantowomechanicznej jest otrzymywanie w wyniku obliczeń prawdopodobieństw, które nie mieszczą się w tych granicach. Ostrą sprzeczność w strukturze cząstek punktowych między ogólną teorią względności a mechaniką kwantową widać po tym, że w obliczeniach otrzymuje się nieskończone prawdopodobieństwa. Teoria strun, jak stwierdziliśmy, usuwa te nieskończoności. Nie wspomnieliśmy jednak o pewnym subtelnym problemie, który pozostał. Wkrótce po stworzeniu teorii strun fizycy zauważyli, że część obliczeń kończy się ujemnymi prawdopodobieństwami. One również wykraczają poza dozwolony zakres. Na pierwszy rzut oka wydawało się więc, że mechanika kwantowa niszczy teorię strun.

Dzięki determinacji i uporowi fizycy znaleźli w końcu przyczynę tego niepokojącego zjawiska. Otóż jeśli struna musi przebywać na dwuwymiarowej płaszczyźnie - takiej jak powierzchnia stołu lub węża ogrodowego - liczba niezależnych kierunków, w których może drgać, maleje do dwóch: prawo-lewo i przód-tył. Każde drganie ograniczone do tej powierzchni stanowi pewną kombinację drgań w owych dwóch kierunkach. Widzimy więc, że struna w Krainie Płaszczaków, wszechświecie węża ogrodowego lub jakimkolwiek innym dwuwymiarowym świecie również jest ograniczona do drgań w dwóch niezależnych kierunkach przestrzennych. Gdyby jednak struna opuściła tę powierzchnię, liczba niezależnych kierunków drgań wzrosłaby do trzech, ponieważ wtedy struna drgałaby także w kierunku góra-dół. Podobnie, we Wszechświecie o trzech wymiarach przestrzennych struna drga w trzech niezależnych kierunkach. Chociaż trudniej to sobie wyobrazić, schemat ten odnosi się także do wszechświata o większej liczbie wymiarów przestrzennych. We wszechświecie takim istnieje jeszcze więcej możliwych kierunków drgań struny.

Zwracamy tak dużą uwagę na drgania struny, ponieważ fizycy stwierdzili, że kłopotliwe wyniki obliczeń wiążą się właśnie z liczbą niezależnych kierunków jej drgań. Ujemne prawdopodobieństwa pojawiały się na skutek niedopasowania wymagań teorii do tego, co zdawała się narzucać rzeczywistość. Z obliczeń wynikało, że gdyby struny drgały w dziewięciu niezależnych kierunkach przestrzennych, wszystkie ujemne prawdopodobieństwa by znikły. Cóż to oznacza? Jeśli teoria strun ma opisywać nasz trójwymiarowy świat, nadal musimy rozwiązać pewne trudności.

Ale czy rzeczywiście? Idąc tropem wyznaczonym pół wieku wcześniej przez Kaluzę i Kleina, zauważamy, że podejście to, być może, wybawi nas z kłopotliwej sytuacji. Skoro struny są wyjątkowo małe, mogą wibrować nie tylko w dużych, rozciągłych wymiarach, ale także w małych i zwiniętych. Mamy więc szansę spełnić wymaganie teorii strun, aby na Wszechświat składało się dziewięć wymiarów przestrzennych, zakładając - za Kaluzą i Kleinem - że oprócz trzech znanych, rozciągłych wymiarów przestrzennych istnieje sześć zwiniętych. W ten sposób uratowano teorię strun, której groziła już eliminacja ze świata użytecznych teorii fizycznych. Co więcej, teoria strun nie tyle postuluje istnienie dodatkowych wymiarów, jak to robili Kaluza, Klein i ich kontynuatorzy, lecz wręcz tego wymaga. Aby miała sens, Wszechświat powinien odznaczać się dziewięcioma wymiarami przestrzennymi i jednym czasowym, czyli w sumie dziesięcioma wymiarami. W ten sposób hipoteza Kaluzy z 1919 roku znajduje swoje najbardziej przekonujące i najlepsze zastosowanie.

Kilka pytań

Nasuwa się w związku z tym kilka pytań. Po pierwsze, dlaczego teoria strun w celu uniknięcia bezsensownych wartości prawdopodobieństwa wymaga istnienia akurat dziewięciu wymiarów przestrzennych? Jest to pytanie, na które w teorii strun chyba najtrudniej odpowiedzieć bez odwoływania się do obliczeń matematycznych. Nikt bowiem nie podał intuicyjnego, prostego wytłumaczenia, dlaczego pojawia się ta właśnie liczba. Fizyk Ernest Rutherford powiedział kiedyś, że jeśli nie potrafimy wyjaśnić wyniku w prosty sposób, bez odwoływania się do matematyki, to tak naprawdę go nie rozumiemy. Wyrażając taką opinię, miał na myśli nie to, że otrzymaliśmy błędny wynik, ale raczej to, iż nie rozumiemy w pełni jego pochodzenia, znaczenia i wypływających z niego wniosków. Niewykluczone, że stwierdzenie Rutherforda jest prawdą w odniesieniu do dodatkowych wymiarów pojawiających się w teorii strun. (Skorzystajmy z tej okazji, aby wtrącić kilka uwag, które przygotują nas na najważniejszą kwestię drugiej rewolucji superstrunowej. Jej przebieg omówiono w rozdziale dwunastym. Okazuje się, iż obliczenia prowadzące do wniosku, że istnieje dziesięć wymiarów czasoprzestrzeni - dziewięć przestrzennych i jeden czasowy - są przybliżone. W połowie lat dziewięćdziesiątych, opierając się na własnych odkryciach i wcześniejszych pracach Michaela Duffa z Uniwersytetu Teksasu oraz Chrisa Hulla i Paula Townsenda z Uniwersytetu w Cambridge, Witten przedstawił dowody na to, że ów przybliżony rachunek w rzeczywistości pomija jeden wymiar przestrzenny. Ku zaskoczeniu większości teoretyków strun Witten dowodził, że teoria strun tak naprawdę wymaga istnienia dziesięciu wymiarów przestrzennych i jednego czasowego, czyli w sumie jedenastu wymiarów. Więcej o tym ważnym wyniku w rozdziale dwunastym).

Po drugie, jeśli z równań teorii strun (a dokładniej: z przybliżonych równań) wynika, że Wszechświat ma dziewięć wymiarów przestrzennych i jeden czasowy, dlaczego trzy wymiary przestrzenne (i jeden czasowy) są duże i rozciągłe, a wszystkie pozostałe - małe i zwinięte? Dlaczego wszystkie nie są albo rozciągłe, albo zwinięte, albo nie mają jakiejś innej postaci? Obecnie nikt nie zna odpowiedzi na te pytania. Jeśli teoria strun jest poprawna, w końcu rozwiążemy tę zagadkę, ale w tej chwili nie rozumiemy teorii strun na tyle, aby osiągnąć zamierzony cel. Nie znaczy to, że nie podejmowano śmiałych prób odpowiedzi na postawione wyżej pytania. Na przykład, przyjmując kosmologiczny punkt widzenia, możemy sobie wyobrazić, że początkowo wszystkie wymiary były ciasno zwinięte, a następnie w wyniku eksplozji przypominającej Wielki Wybuch trzy wymiary przestrzenne i jeden czasowy rozwinęły się i rozszerzyły do obecnych rozmiarów, a inne pozostały małe. Jak się przekonamy w rozdziale czternastym, istnieją przybliżone wyjaśnienia, dlaczego tylko trzy wymiary przestrzenne rosną, trzeba jednak przyznać, że jeszcze ich nie dopracowano. W dalszych rozważaniach przyjmiemy założenie, że zgodnie z tym, co obserwujemy wokół siebie, wszystkie wymiary przestrzenne, z wyjątkiem trzech, są zwinięte. Główny cel współczesnych badań polega na zyskaniu pewności, że stwierdzenie to wywodzi się z samej teorii.

Po trzecie, jeśli przyjmiemy za konieczne istnienie wielu dodatkowych wymiarów, czy jest możliwe, że niektóre z nich to dodatkowe wymiary czasowe, a nie przestrzenne? Ewentualność ta wydaje się naprawdę dziwaczna. Wszyscy intuicyjnie rozumiemy, co znaczy dla Wszechświata posiadanie dodatkowych wymiarów przestrzennych, ponieważ w naszym świecie stale mamy do czynienia z tą wielością - mianowicie z trzema wymiarami. Z czym jednak wiązałoby się istnienie wielu czasów? Czy jeden z nich pokrywałby się z czasem takim, jakiego obecnie doświadczamy psychologicznie, a drugi różniłby się w jakiś sposób od niego?

Możliwość ta zadziwia jeszcze bardziej, gdy myślimy o zwiniętym wymiarze czasowym. Na przykład mała mrówka, spacerując wzdłuż dodatkowego wymiaru przestrzennego zwiniętego w okrąg, stwierdzi, że za każdym razem po przejściu pełnego okręgu wraca do tego samego miejsca. Nie stanowi to żadnej tajemnicy, ponieważ z naszego doświadczenia wynika, że można wracać do danego miejsca w przestrzeni tak często, jak się chce. Gdyby jednak zwiniętym wymiarem był wymiar czasowy, zatoczenie kręgu oznaczałoby powrót po pewnym czasie do chwili wcześniejszej. To, oczywiście, nie mieści nam się w głowie. Znany nam czas to wymiar, w którym możemy się poruszać tylko w jednym kierunku. Nigdy nie wracamy do minionej chwili. Możliwe, że zwinięte wymiary czasowe mają zupełnie inne właściwości niż rozciągły wymiar czasowy, który zgodnie z naszymi wyobrażeniami istnieje od chwili stworzenia Wszechświata aż do teraźniejszości. W przeciwieństwie jednak do dodatkowych wymiarów przestrzennych wprowadzenie nowych i nieznanych wcześniej wymiarów czasowych wymagałoby od nas jeszcze większej zmiany myślenia. Niektórzy teoretycy zastanawiali się nad możliwością włączenia do teorii strun dodatkowych wymiarów czasowych, ale jak na razie sytuacja pozostaje niejasna. W rozważaniach na temat teorii strun ograniczymy się do konwencjonalnego podejścia, zgodnie z którym wszystkie zwinięte wymiary są wymiarami przestrzennymi. Nie wykluczamy jednak, że intrygująca możliwość istnienia nowych wymiarów czasowych ma szansę odegrać pewną rolę w przyszłych odkryciach.

Fizyczne wnioski z dodatkowych wymiarów

W ciągu lat badań prowadzonych od momentu opublikowania artykułu Kaluzy stało się jasne, że chociaż wszystkie proponowane przez fizyków dodatkowe wymiary muszą być mniejsze niż te, które bezpośrednio "oglądamy" (gdyż ich dotąd nie dostrzegliśmy), mają one pośredni wpływ na obserwowane przez nas prawa fizyki. W teorii strun ten związek między mikroskopowymi właściwościami przestrzeni a obserwowanymi prawami fizycznymi widać szczególnie wyraźnie.

Aby ułatwić zrozumienie całego problemu, przypomnijmy, że masy i ładunki cząstek są w teorii strun określone przez rezonansowe drgania struny. Wyobraźmy sobie ruchomą, oscylującą strunę, a natychmiast stanie się dla nas jasne, że drgania te ulegają wpływom jej przestrzennego otoczenia. Za przykład niech posłużą fale oceanu. Na otwartym morzu izolowane wzory drgań powstają stosunkowo swobodnie i rozchodzą się w rozmaite strony. Podobnie dzieje się z drganiami struny, gdy porusza się ona w dużych, rozciągłych wymiarach przestrzennych. Jak opisano w rozdziale szóstym, struna taka w dowolnej chwili równie swobodnie oscyluje w każdym z rozciągłych kierunków. Jeśli jednak fala oceanu przejdzie przez jakieś ciasne miejsce, dokładna postać jej ruchu z pewnością się zmieni pod wpływem, na przykład, głębokości wody, położenia i kształtu napotkanych skał oraz kanałów i tak dalej. Innym przykładem jest piszczałka organów lub róg. Dźwięki wytwarzane przez każdy z tych instrumentów powstają bezpośrednio na skutek pojawienia się we wnętrzu danego instrumentu drgających w rezonansie strumieni powietrza. Drgania te są z kolei określone przez rozmiary i kształt instrumentu, przez który przechodzą strumienie powietrza. Zwinięte wymiary przestrzenne wywierają podobny wpływ na rezonansowe drgania struny. Ponieważ małe struny drgają we wszystkich wymiarach przestrzennych, sposób zwinięcia i wzajemnego ustawienia dodatkowych wymiarów w znaczący sposób wpływa na strunę i nakłada duże ograniczenia na możliwe rezonansowe wzory drgań. Wzory te, w dużej mierze wyznaczone przez geometrię dodatkowych wymiarów, tworzą widmo możliwych właściwości cząstek, które to właściwości obserwujemy w znanych, rozciągłych wymiarach. Geometria wyższych wymiarów wyznacza więc podstawowe cechy fizyczne, takie jak masy i ładunki cząstek, obserwowane w zwykłych trzech dużych wymiarach przestrzennych, znanych z codziennego doświadczenia.

Stwierdzenie to jest niezwykle ważne. Powtórzymy je więc raz jeszcze. Zgodnie z teorią strun Wszechświat składa się z małych strun, których rezonansowe drgania są mikroskopowym źródłem mas cząstek i ładunków sił. Teoria strun wymaga również istnienia dodatkowych wymiarów przestrzennych, które muszą być zwinięte do bardzo małych rozmiarów, skoro nigdy ich nie widzieliśmy. Ale mała struna może badać jedynie przestrzeń w małej skali. Gdy struna się porusza i wibruje, geometryczna postać dodatkowych wymiarów decyduje o właściwościach jej rezonansowych drgań. Ponieważ owe wzory drgań widzimy w postaci mas i ładunków cząstek elementarnych, dochodzimy do wniosku, że te podstawowe cechy Wszechświata są w dużej mierze określone przez geometryczne rozmiary i kształt dodatkowych wymiarów. Jest to jedno z najdonioślejszych odkryć teorii strun.

Skoro dodatkowe wymiary w tak dużym stopniu kształtują podstawowe fizyczne właściwości Wszechświata, powinniśmy z niesłabnącym uporem dążyć do tego, by zrozumieć, jak owe wymiary wyglądają.

Jak wyglądają zwinięte wymiary?

Dodatkowych wymiarów przestrzennych pojawiających się w teorii strun z pewnością nie można poukładać byle jak. Równania tej teorii w znacznym stopniu wyznaczają ich geometryczną postać. W 1984 roku Philip Candelas z Uniwersytetu Teksasu w Austin, Gary Horowitz i Andrew Strominger z Uniwersytetu Kalifornijskiego w Santa Barbara oraz Edward Witten udowodnili, że warunki te spełnia pewna szczególna klasa sześciowymiarowych kształtów geometrycznych. Znamy je jako przestrzenie (lub kształty) Calabiego-Yau. Nazwę nadano na cześć dwóch matematyków, Eugenio Calabiego z Uniwersytetu Pensylwanii i Shing-Tunga Yau z Uniwersytetu Harvarda, których badania w pokrewnej dziedzinie, jeszcze przed powstaniem teorii strun, w ogromnym stopniu przyczyniły się do zrozumienia tych przestrzeni. Chociaż matematyka opisująca przestrzenie Calabiego-Yau jest skomplikowana, łatwo pokazać ich wygląd na rysunku.


Rycina 8.9 przedstawia jedną z przestrzeni Calabiego-Yau. Patrząc na rysunek, pamiętajmy o pewnych nieuniknionych ograniczeniach. Na dwuwymiarowej kartce papieru bowiem przedstawiono kształt sześciowymiarowy, a to spowodowało wprowadzenie znacznych zniekształceń. Niemniej rycina 8.9 oddaje ogólny wygląd przestrzeni Calabiego-Yau. Kształt przedstawiony na rycinie 8.9 to jeden z dziesiątków tysięcy przykładów tej przestrzeni, które spełniają skomplikowane wymagania teorii strun co do dodatkowych wymiarów. Chociaż przynależność do klubu liczącego dziesiątki tysięcy członków nie wydaje się zbytnim wyróżnieniem, miejmy świadomość, że liczba kształtów matematycznie możliwych jest nieskończona. Z tego punktu widzenia przestrzenie Calabiego-Yau rzeczywiście należą do rzadkości.

Wyobraźmy sobie teraz, że każdą ze sfer przedstawiających zwinięte wymiary (por. ryc. 8.7) zastępujemy przestrzenią Calabiego-Yau. Oznacza to, że zgodnie z teorią strun w każdym punkcie trzech znanych nam rozciągłych wymiarów znajduje się sześć nieznanych dotąd wymiarów, ciasno zwiniętych do postaci jednego ze skomplikowanych kształtów, przypominających ten, który pokazano na rycinie 8.10.
Wymiary te są nieodłączną częścią struktury przestrzennej. Istnieją wszędzie. Jeśli na przykład zatoczymy ręką łuk, poruszamy nią nie tylko w trzech rozciągłych wymiarach, ale także w tych zwiniętych. Zwinięte wymiary są jednak na tyle małe, że gdy ruszamy ręką, obiegamy je olbrzymią liczbę razy, powracając wielokrotnie do punktu wyjścia. Ich mała wielkość sprawia, że nie ma w nich miejsca na ruch tak dużego obiektu, jak nasza ręka. Ruch ten się uśrednia. Po zatoczeniu łuku nie zdajemy sobie sprawy z podróży odbytej w zwiniętych wymiarach Calabiego-Yau.

Jest to zaskakująca właściwość teorii strun. Jeśli jednak mamy umysł praktyczny, musimy wrócić do zasadniczej kwestii, która pojawiła się w naszych rozważaniach. Teraz, kiedy lepiej wyobrażamy sobie, jak wyglądają dodatkowe wymiary, zastanówmy się nad cechami fizycznymi wynikającymi z drgań strun w tych wymiarach i związkiem tych właściwości z wynikami doświadczeń. To najważniejsze pytanie, przed jakim stoi teoria strun.

 

Brian Greene

Fragment książki „Piękno Wszechświata”

Przełożyli: Ewa L. Łokas i Bogumił Bieniok

Wydawnictwo Prószyński i S-ka SA

---