Macierze i Wyznaczniki
Przykład: W fabryce wytwarza się n różnych produktów złożonych z części produkowanych na m stanowiskach. Plan określa ilość godzin potrzebnych na wykonanie tej części jednostki danego produktu, która przypada na dane stanowisko. Jak krótko można by zapisać ten plan?
• Niech aij oznacza ilość godzin, w ciągu których ma być wykonana na stanowisku i , gdzie ![]()
, część produktu o numerze j , gdzie ![]()
.
Wówczas pojawia się zapis (w formie następującej tablicy):
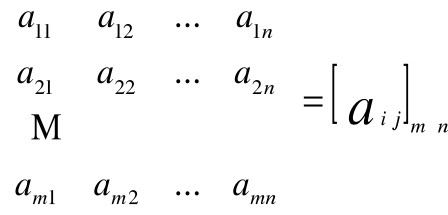
oznacza: i-ty wiersz
oznacza: j-tą kolumnę
To jest macierz prosta
o wymiarach mxn
Ten nowy obiekt
będziemy nazywać macierz(-ą) i oznaczać dużymi literami A, B, C.
Stąd w/w macierz oznaczamy:
A=[a i j]m×n
Definicja Macierzą o wymiarze m×n nad ciałem K (bądź krótko: macierzą) nazywamy odwzorowanie
T:{1,2,3,...,m}×{1,2,...,n} K.
Np. A=[a i j]m×n , gdzie a i j = T(i,j) dla ![]()
,![]()
.
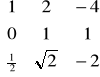
-- macierz o wymiarze 3×3
Przykład: Macierz przekształcenia liniowego. Niech dane będą duże przestrzenie linowe Rn i Rm nad ciałem R generowane przez bazy kanoniczne, odpowiednio: ē1,ē2,...,ēn oraz ē'1,ē'2,...,ē'm
Niech T będzie odwzorowaniem liniowym Rn w Rm oraz ![]()
.
Wówczas
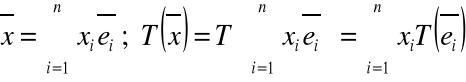
(1)
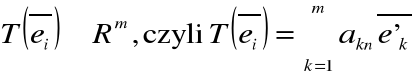
ale (2)
Ze związków (1) i (2) otrzymujemy:
![]()
(3)
![]()
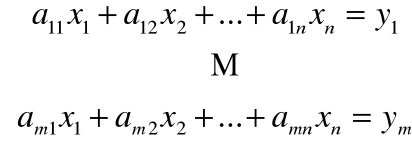
Oznaczając ![]()
,(4) otrzymujemy z (3) i (4) następujący układ równań:
Uwaga! Współczynnik a i j przy niewiadomych: x1,x2,...,xn tworzą prostokątną tablicę (macierz)
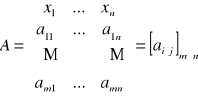
zwaną macierzą odwzorowania (przekształcenia) liniowego T: Rn Rm.
Szczególne rodzaje macierzy.
Niech A=[a i j]m×n ,gdzie ![]()
K-ciało (w szczegól.: K=R, bądź K=C)
Macierz A nazywa się macierzą kwadratową (krótko: kwadratową), gdy m=n; wówczas n nazywa się stopniem macierzy.
• W szczególności macierz przekształcenia liniowego T: Rn Rm jest kwadratowa stopnia n.
Macierz przekształcenia liniowego

nazywa się macierzą jednostkową stopnia n, którą oznaczamy En ; przy czym:
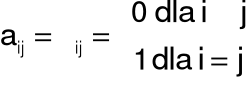
En =[a i j]m×n , gdzie
||

Symbol
Kronckera

Macierz A=[a i j]m×n,gdzie
nazywa się macierzą diagonalną stopnia n
Macierz AT=[b i j]m×n ,
gdzie b i j =a i j ^ A=[a i j ]mxn nazywamy macierzą transponowaną do macierzy A o wymiarze mxn.
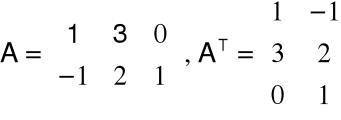
Np.
Działania na macierzach
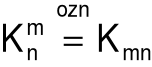
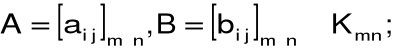
Niech oznacza zbiór macierzy o wymiarach mxn i wyrazach ciała K.
![]()
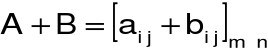
Definicja Sumę macierzy A i B o wymiarze mxn będziemy oznaczać A+B przyczym:
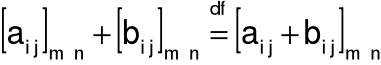
Stąd :
Definicja Iloczyn skalarny λ i macierzy A o wymiarach mxn będziemy oznaczać λ•A, przy czym:
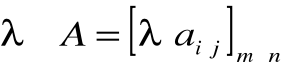
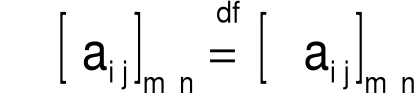
Stąd:
Np. Znaleźć A+B oraz (-2)A, gdy
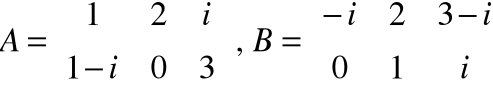
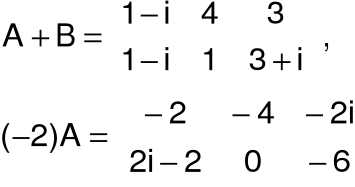
Zatem po zastosowaniu w/w definicji otrzymujemy:
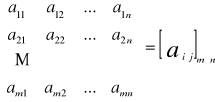
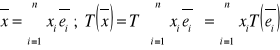
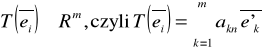
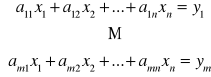
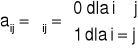
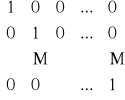
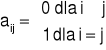
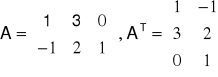
![]()
![]()
![]()
![]()
![]()
![]()
![]()
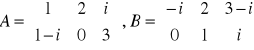
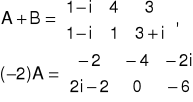
Wyszukiwarka
Podobne podstrony:
Macierze i Wyznaczniki2, A) STUDIA INŻYNIERSKIE, Matematyka, matematyka
Macierze i Wyznaczniki3, A) STUDIA INŻYNIERSKIE, Matematyka, matematyka
Funkcja pierwotna, A) STUDIA INŻYNIERSKIE, Matematyka, matematyka
Całki funkcji elementarnych, A) STUDIA INŻYNIERSKIE, Matematyka, matematyka
wyznaczniki, Studia TOŚ, matematyka zadania rok I
Macierze i wyznaczniki, Politechnika Poznańska, Elektrotechnika, Matematyka, semestr 2
Matematyka 16.10.2010 macierze, chomik, studia, STUDIA - 1 rok, Matematyka
Sciaga Macierz-odwrotna, studia, matematyka
ZAdania z matematyki, MACIERZE I WYZNACZNIKI-2010, MACIERZE I WYZNACZNIKI - ZADANIA
md 3z, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna
md 2zb, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna, pysiak - pd
md 3za, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna, pysiak - pd
Macierze, Informatyka - studia, Matematyka Dyskretna, semestr IV
sciaga md, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna
md 2z, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna
w10 macierze działania wyznaczniki, Finanse SGGW, Matematyka
dyskretna termin1, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna
md lipiec 2005, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna
md luty 2005, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna
więcej podobnych podstron