Wyznacznik o dwóch jednakowych wierszach (bądź kolumnach) jest równy zero.
Wspólny czynnik wszystkich elementów danego wiersza (bądź kolumny) można wyłączyć przed znak wyznacznika.
Wyznacznik, którego dwa wiersze (bądź kolumny) utworzone są z elementów odpowiednio proporcjonalnych jest równy zero.Wartość wyznacznika nie ulegnie zmianie, jeśli do elementów jednego wiersza (bądź kolumny) dodamy odpowiednio elementy innego wiersza (bądź kolumny) pomnożone przez dowolną liczbę.
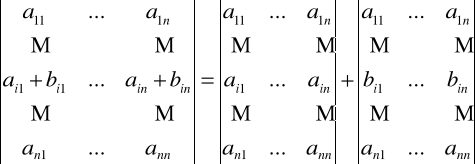
Twierdzenie Cauchy'ego : Jeżeli A,B∈Knm , to Det AB =Det A*Det B.
Det (tA)= tn * DetA, gdy t∈R, A∈Knm
.
:
Przekształcenia elementarne macierzy
Definicja Niech A=[a i j]m×n
Przekształceniami elementarnymi I rodzaju, macierzy A, nazywamy następujące działania:
pomnożenie wszystkich elementów dowolnego wiersza przez liczbę różną od zera;
zamianę miejscami (przestawienie) dwóch dowolnych wierszy macierzy
dodanie do wszystkich elementów dowolnego wiersza odpowiednich elementów innego wiersza pomnożonych przez dowolną liczbę różną od zera.
• Działania analogiczne do 1) -3) na kolumnach macierzy nazywamy przekształceniami elementarnymi II rodzaju.
• Korzystając z własności wyznaczników dowodzi się między innymi, że:
Przy wykonywaniu przekształceń elementarnych macierzy nie zmieniamy rzędu macierzy.
Stopień podmacierzy IK macierzy danej w postaci kanonicznej jest równy rzędowi tej macierzy.
Definicja Każdą macierz (w szczegól. kwadratową) B utworzoną z macierzy A poprzez skreślenie w niej pewnej liczby wierszy i kolumn nazywamy podmacierzą macierzy A.
Stąd w szczególności:
B jest stopnia od 1 do min(n,m), gdzie A jest o wymiarach mxn;
B=A jest podmacierzą macierzy A
Postać kanoniczna macierzy
Definicja Każdą macierz A=[a i j]m×n można za pomocą przekształceń elementarnych I rodzaju (bądź II rodzaju) przekształcić w macierz postaci:
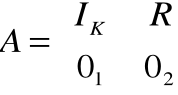
,która jest nazywana postacią kanoniczną (bądź bazową) danej
macierzy, przy czym IK jest podmacierzą jednostkową stopnia K, K ≤min(n,m), jest podmacierzą zwaną macierzą resztową, zaś 01,02 - podmacierze zerowe.
Definicja Macierze otrzymane z danej macierzy w wyniku przekształceń elementarnych nazywamy macierzami równoważnymi.
Np. Wyznaczyć rząd macierzy A, gdy
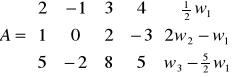
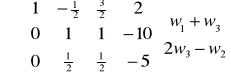
E2 R
Stąd rz(A)=rz(E2)=2
01 02
Ćwiczenie Sprawdź, że rz(B)=2, gdy:
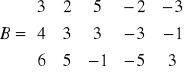
III Definicja rzędu macierzy : Rzędem macierzy niezerowej A o wymiarze nxm nazywamy najwyższy stopień nieosobliwej podmacierzy B macierzy A.
Np.
Wyznaczyć rząd macierzy A za pomocą wyznaczników, gdy:

Dla wyznaczenia rzędu macierzy A należy znaleźć podmacierz B macierzy A stopnia co najwyżej 3. Stąd:
- podmacierzy stopnia 3 będzie:
- podmacierzy stopnia 2 będzie:
- podmacierzy stopnia 1 będzie:
Sprawdź, że rz(A)=2.
Definicja Macierz kwadratowa A-1 spełniająca rowność AA-1=A-1A=En nazywamy macierzą odwrotną do macierzy A stopnia n.
Twierdzenie: Jeśli macierz A stopnia n jest nieosobliwa, to istnieje do niej macierz odwrotna A-1 , przy czym:
, gdzie AD jest macierzą dopełnień algebraicznych
elementów macierzy A.
Przykład: Wyznaczyć macierz odwrotną (o ile istnieje) do macierzy
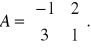
Plan rozwiązania.
Badam nie osobliwość macierzy A: DetA= -1-6= -7≠0, czyli A jest macierzą nieosobliwą.
Wobec spełnionego założenia w/w to istnieje A-1, przyczym:
• Wyznaczam macierz
A11=(-1)1+1*|1|=1 ; A12=(-1)1+2*|3|= -3
A12=(-1)2+1*|2|= -2 ; A22=(-1)2+2*|-1|= -1
Stąd:
• Wyznaczam A-1
Układy równań liniowych
Rozważmy układ m równań liniowych o n niewiadomych:
(1)
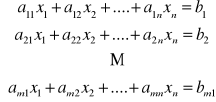
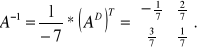
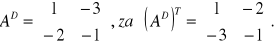
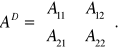
![]()
![]()
![]()
![]()
![]()

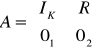
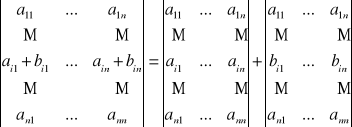
Wyszukiwarka
Podobne podstrony:
Macierze i Wyznaczniki, A) STUDIA INŻYNIERSKIE, Matematyka, matematyka
Macierze i Wyznaczniki2, A) STUDIA INŻYNIERSKIE, Matematyka, matematyka
Funkcja pierwotna, A) STUDIA INŻYNIERSKIE, Matematyka, matematyka
Całki funkcji elementarnych, A) STUDIA INŻYNIERSKIE, Matematyka, matematyka
wyznaczniki, Studia TOŚ, matematyka zadania rok I
Macierze i wyznaczniki, Politechnika Poznańska, Elektrotechnika, Matematyka, semestr 2
Matematyka 16.10.2010 macierze, chomik, studia, STUDIA - 1 rok, Matematyka
Sciaga Macierz-odwrotna, studia, matematyka
ZAdania z matematyki, MACIERZE I WYZNACZNIKI-2010, MACIERZE I WYZNACZNIKI - ZADANIA
md 3z, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna
md 2zb, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna, pysiak - pd
md 3za, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna, pysiak - pd
Macierze, Informatyka - studia, Matematyka Dyskretna, semestr IV
sciaga md, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna
md 2z, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna
w10 macierze działania wyznaczniki, Finanse SGGW, Matematyka
dyskretna termin1, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna
md lipiec 2005, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna
md luty 2005, wisisz, wydzial informatyki, studia zaoczne inzynierskie, matematyka dyskretna
więcej podobnych podstron