MACIERZE

Niech ustalone będą dwie liczby naturalne m, n.

definicja

Macierzą o wyrazach rzeczywistych i wymiarach m na n nazywamy funkcję

tzn. przyporządkowanie każdej parze (i,j) liczb naturalnych i=1,2,...,m, j=1,2,...,n dokładnie jednej liczby rzeczywistej a_ij.

Macierz taką zapisujemy w tablicy o m wierszach i o n kolumnach

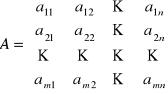
lub krótko
.

Liczby a_ij nazywamy wyrazami macierzy.

Wyrazy
tworzą i-ty wiersz macierzy A.

Wyrazy
tworzą j-tą kolumnę macierzy A.

Macierz, której wszystkie elementy są równe zero nazywamy zerową i oznaczamy 0.

Zbiór wszystkich macierzy o wyrazach rzeczywistych i wymiarach m na n oznaczmy przez
.

Jeśli m=n, to macierz nazywamy kwadratową.

macierze kwadratowe

Jeśli liczba wierszy jest równa liczbie kolumn i wynosi n, to macierz nazywamy macierzą kwadratową stopnia n.

Wyrazy a₁₁, a₂₂, a₃₃,...,a_nn tworzą główną przekątną macierzy kwadratowej stopnia n.

Macierz kwadratową, w której wszystkie wyrazy poza główną przekątną są równe zero nazywamy macierzą diagonalną.

Macierz diagonalną, której wyrazy na głównej przekątnej są równe jedności nazywamy macierzą jednostkową.

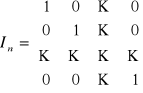
Macierz kwadratową, której wszystkie wyrazy stojące pod (nad) główną przekątną są równe zero nazywamy macierzą trójkątną górną (dolną).

macierz trójkątna górna

Działania na macierzach

Macierze
i
o jednakowych wymiarach są równe, piszemy
, jeżeli
dla
,
.

Sumą macierzy
i
o jednakowych wymiarach nazywamy macierz
, którą otrzymujemy dodając do każdego wyrazu macierzy A odpowiedni wyraz macierzy B.

Analogicznie określamy różnicę dwóch macierzy
.

Iloczynem macierzy
przez liczbę s nazywamy macierz
, którą otrzymujemy, mnożąc każdy wyraz macierzy A przez liczbę s.

Iloczynem macierzy
przez macierz
nazywamy macierz
, której każdy wyraz
jest iloczynem skalarnym i-tego wiersza macierzy A przez j-tą kolumnę macierzy B.

,
.

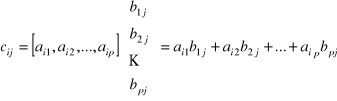
Możemy wykonać mnożenie AB tylko takich macierzy A, B, dla których liczba kolumn macierzy A jest równa liczbie wierszy macierzy B. W rezultacie mnożenia otrzymujemy macierz, która ma tyle wierszy co macierz A i tyle kolumn co macierz B.

Przez n-tą potęgę Aⁿ macierzy kwadratowej A rozumiemy iloczyn n macierzy A.

Własności działań na macierzach

Zakładamy, że macierze A, B, C mają takie wymiary, aby działania były wykonalne,

s,t oznaczają liczby rzeczywiste.

1. Dodawanie macierzy jest przemienne i łączne.

,

2. Mnożenie macierzy przez liczbę jest łączne i rozdzielne względem dodawania liczb i dodawania macierzy tzn.

,
,

3. Mnożenie macierzy przez macierz nie jest przemienne
.

4. Mnożenie macierzy przez macierz jest łączne i rozdzielne względem dodawania.

,
,

5. Wynikiem mnożenie macierzy A przez macierz jednostkową jest macierz A.

,

Macierzą transponowaną macierzy
nazywamy macierz
, którą

otrzymujemy zapisując kolejne wiersze macierzy A jako kolumny macierzy
.

Wyznacznik macierzy kwadratowej

Wyznacznik macierzy kwadratowej A jest liczbą, którą oznaczamy symbolem detA lub
.

Def: (indukcja ze względu na stopień macierzy tzn. obliczenie wyznacznika macierzy stopnia n wymaga obliczenia wyznacznika macierzy stopnia
.

Wyznacznikiem macierzy kwadratowej A stopnia n nazywamy liczbę zdefiniowaną poniżej:

1. Jeżeli
.

2. Jeżeli
, to

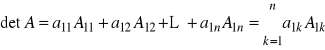
gdzie
jest liczbą równą iloczynowi
przez wyznacznik macierzy stopnia
powstałej z macierzy A przez wykreślenie i-tgo wiersza i j - tej kolumny.

Liczbę
nazywamy dopełnieniem algebraicznym elementu
.

Zatem

1. W przypadku gdy
, tzn. gdy macierz zawiera tylko jeden wyraz przyjmujemy, że wyznacznik jest wartością tego wyrazu.

2. W przypadku gdy
wyznacznik jest równy sumie wyrazów pierwszego wiersza pomnożonych przez dopełnienia algebraiczne tych wyrazów.

Tw: Laplace'a (rozwinięcie wyznacznika względem dowolnego wiersza lub dowolnej kolumny)

Dla każdego i,
zachodzi równość

.

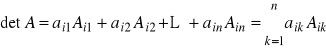
Dla każdego j,
zachodzi równość

.

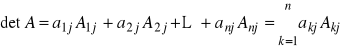
Wyznacznik macierzy kwadratowej jest równy sumie wyrazów dowolnego wiersza lub dowolnej kolumny pomnożonych przez dopełnienia algebraiczne tych wyrazów.

WŁASNOŚCI WYZNACZNIKÓW

1.

2. Jeżeli każdy element pewnego wiersza lub kolumny macierzy jest równy zero, to wyznacznik tej macierzy jest równy zero.

3. Jeżeli macierz B powstaje z macierzy A przez zamianę miejscami dwóch wierszy lub dwóch kolumn, to

.

4. Jeżeli dwa wiersze macierzy lub dwie kolumny są proporcjonalne (w szczególności identyczne), to wyznacznik tej macierzy jest równy zero.

5. Jeżeli elementy pewnego wiersza lub pewnej kolumny mają wspólny czynnik, to można go wyciągnąć przed wyznacznik.

Np.

= ၬ

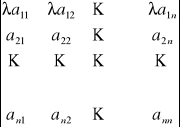
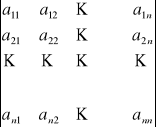
6. Jeżeli do elementów wiersza macierzy lub do kolumny dodamy odpowiednie elementy innego wiersza lub innej kolumny pomnożone przez dowolną liczbę, to wyznacznik macierzy nie ulegnie zmianie.

7. Jeżeli w macierzy wszystkie elementy znajdujące się pod przekątną główną są równe zeru, to wyznacznik tej macierzy jest równy iloczynowi elementów głównej przekątnej.

Tw: Cauchy'ego

Jeżeli macierze kwadratowe A, B są tego samego stopnia, to

.

Def:

Macierz kwadratową A nazywamy:

osobliwą, gdy detA=0

nieosobliwą, gdy detA≠0.

Z tw. Cauchy'ego wnioskujemy, że iloczyn macierzy nieosobliwych jest macierzą nieosobliwą.

---