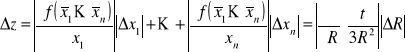SPRAWOZDANIE Z LABORATORIUM FIZYKI 1 NR 12 Z DNIA 18.11.1998 PT :

„BADANIE PROCESÓW RELAKSACYJNYCH W OBWODACH ELEKTRYCZNYCH”

Procesem relaksacji nazywamy proces dochodzenia układu do stanu równowagi, związanego z rozpraszaniem (przekazywaniem) energii przez układ do otoczenia. Na przykład: stygnięcie ciał, rozlewanie się kropli wody na płaskiej powierzchni. Do tego stanu można dojść również na drodze zwiększenia energii danego układu np. poprzez nagrzewanie ciała w piecu lub ładowanie kondensatora po podłączeniu do jego zacisków źródła prądu. Proces ten wywołany zmianą warunków środowiska zewnętrznego jest dość mocno rozciągnięty w czasie, a zmiany energii (dE) przebiegają w charakterystyczny dla tych procesów sposób.

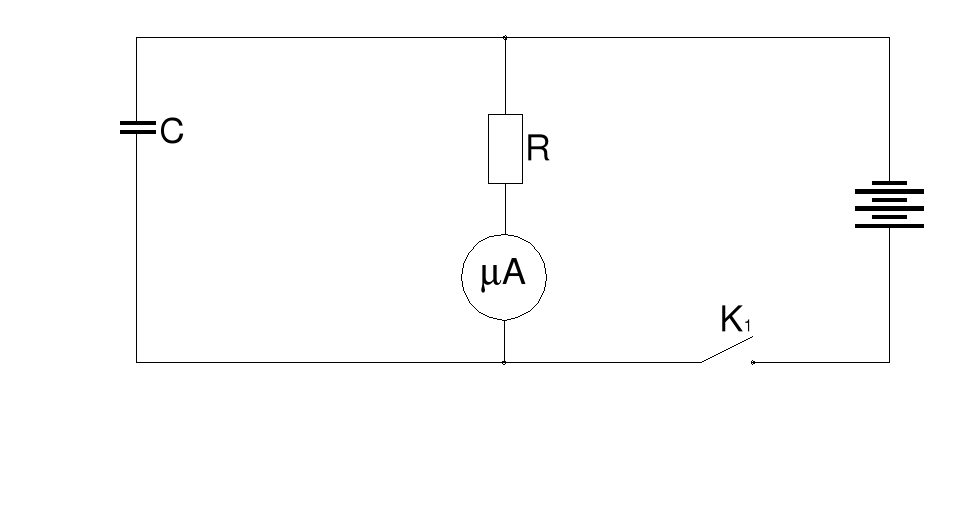
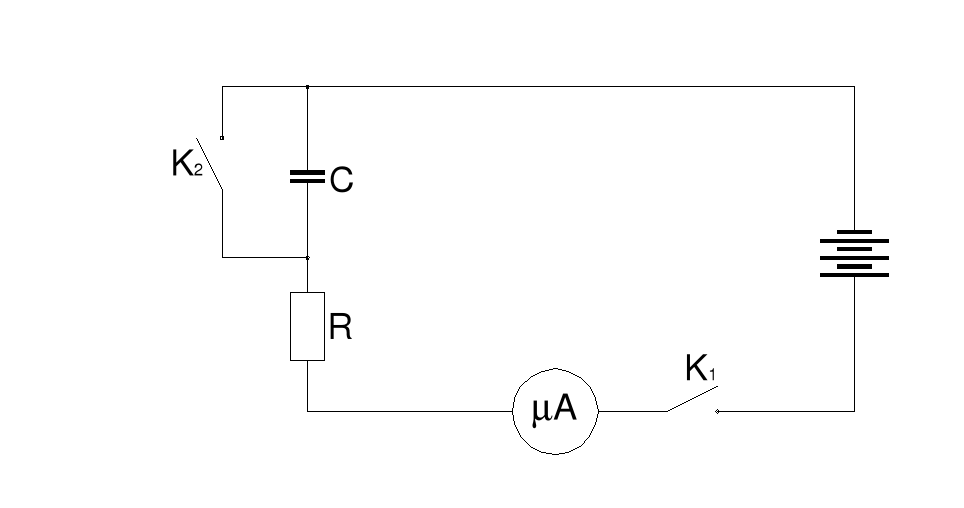
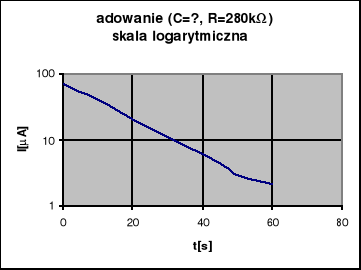
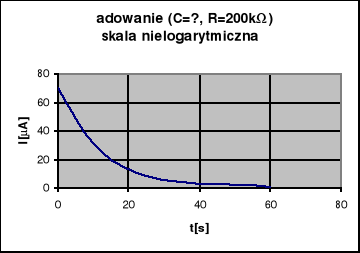
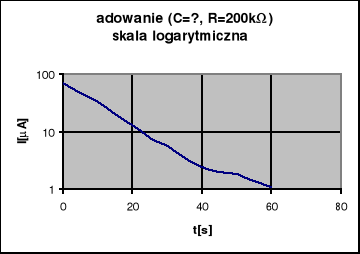
Podczas ćwiczeń laboratoryjnych dotyczących tego zagadnienia mieliśmy za zadanie zebrać dane do wykonania wykresu prądów rozładowania i ładowania. Doświadczenia te polegały na odczytywaniu wartości wskazywanych przez mikroamperomierz w 5-sekundowych odstępach czasu. W tym celu należało połączyć dwa układy elektryczne (rys.1 - dla ładowania kondensatora, rys. 2 - dla rozładowywania kondensatora).

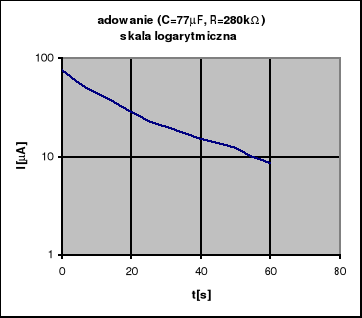
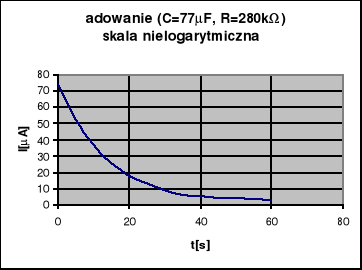
Dokonaliśmy po 6 pomiarów ładowania przy użyciu znanego oporu (280 ± 14)*10³ Ω dwóch kondensatorów: pierwszy elektrolityczny o pojemności (88.5 ± 4,4)μF ,drugi kondensator o nieznanej pojemności .

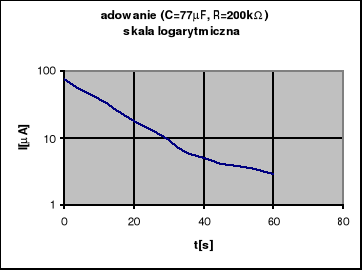
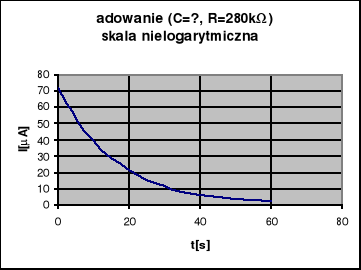
Dla rozładowania wykonaliśmy 6 pomiarów dla jednego kondensatora (o nieznanej pojemności ),przy znanym oporze używając tego samego opornika co przy ładowaniu kondensatora. Wyniki podane zostały w tabeli 1. Na jej podstawie można obliczyć objętość kondensatora o nieznanych parametrach. Dokonuje się tego za pomocą wzoru:

gdzie:

t — czas po jakim zakończono pomiary dla danego oporu i kondensatora (czyli wtedy,
gdy wartość kolejnego pomiaru spada do około 5% pierwszego z nich).

τ — czas relaksacji (t/3)

C — szukana pojemność kondensatora

R — wartość oporu wchodzącego w skład układu (por. rys. 1 i rys. 2)

Po zestawieniu wyników pomiarów objętości z wartościami znanymi, podanymi na obudowie kondensatora okazało się, że są one w granicach dopuszczalnego błędu. Dlatego też należy sądzić, że podobne pomiary wykonane dla kondensatora o nieznanej objętości są wiarygodne (tabela 2)

Tabela 1

Czas.

Ładowanie kondensatora

C=77μF R=280kΩ

C=77μF R=200kΩ

C=? R=280kΩ

C=? R=200kΩ

Rozładowanie kondensatora

C=? R=280kΩ

C=? R=200kΩ

0 s.

74 μA

74 μA

72 μA

70 μA

69 μA

72 μA

5 s.

55 μA

52 μA

53 μA

48 μA

51 μA

50 μA

10 s.

44 μA

38 μA

40 μA

32 μA

39 μA

35 μA

15 s.

35 μA

26 μA

29 μA

20 μA

30 μA

23 μA

20 s.

28 μA

18 μA

21 μA

13 μA

23 μA

16 μA

25 s.

23 μA

18 μA

21 μA

8 μA

16,5

10 μA

30 s.

20 μA

9 μA

11 μA

5,5 μA

13 μA

4,5 μA

35 s.

17 μA

6 μA

8 μA

3,5 μA

10 μA

4,5 μA

40 s.

15 μA

5 μA

6 μA

2,5 μA

7,5 μA

3 μA

45 s.

13,5 μA

4 μA

4,5 μA2

2 μA

5,5 μA

2 μA

50 s.

12 μA

3,7 μA

3 μA

1,8 μA

4 μA

1,3 μA

55 s.

10 μA

3,4 μA

2,5 μA

1,4 μA

3 μA

1 μA

60 s.

8,5 μA

2,9 μA

2,1 μA

1,1 μA

2,3 μA

0,8 μA

Tabela 2

Wartość podana (znana, nominalna)	Wartość obliczona
77μF ± 5% (± 3,9μF)	77,381μF ± 3,571μF (R=280kΩ)
		75μF ± 3,75μF (R=200kΩ)
	brak	59,5238μF ± 2,976μF (R=280Ω)
		58,3333μF ± 2,971μF (R=200Ω)

Wartości otrzymane podczas pomiarów dla rozładowania kondensatora są identyczne, gdyż wzór, wg którego były one liczone jest niezależny od samych zmierzonych wartości. Na ich podstawie można jedynie stwierdzić jakie t przyjąć przy obliczeniach. Błędy policzyliśmy metodą różniczki zupełnej.

gdzie:

t — czas po jakim zakończono pomiary dla danego oporu i kondensatora (czyli wtedy,
gdy wartość kolejnego pomiaru spada do około 5% pierwszego z nich).

R — wartość oporu włączonego w układ

ΔR — błąd systematyczny objętości oporu znajdującego się w układzie

Wartości obliczone wg powyższego równania zawiera tabela 2. Powyższe wykresy obrazują wcześniej opisany proces ładowania (rozładowanie kondensatora ma prawie identyczny wykres).

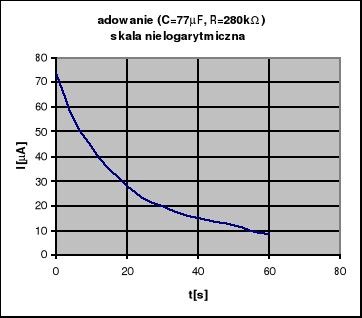
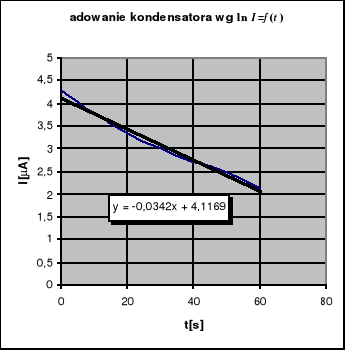
Pojemności tych kondensatorów można obliczyć graficzną metodą rysując wykres

dla każdego z wykonanych eksperymentów. Jeden z nich jest wykonany poniżej:

Grubsza linia jest aproksymacją wykresu, której wzór mieści się na szarym polu.

Czas relaksacji obliczany jest wg wzoru: τ= -1/a, gdzie a to współczynnik prostej aproksymującej wykres powyższy. Do tego celu użyliśmy komputera i wynikiem tej współpracy są następujące wyniki wraz z błędami w dokładności 3s:

Ładowanie kondensatora

C=77μF R=280kΩ

C=77μF R=200kΩ

C=? R=280kΩ

C=? R=200kΩ

Rozładowanie kondensatora

C=? R=280kΩ

C=? R=200kΩ

czas τ.

29,2 s

17,7 s

16,4 s

14,0 s

17,6 s

12,8 s

błąd

± 4*10^-3s

± 1*10^-2s

± 3*10^-3s

± 1*10^-2s

± 1*10^-3s

± 3*10^-3s

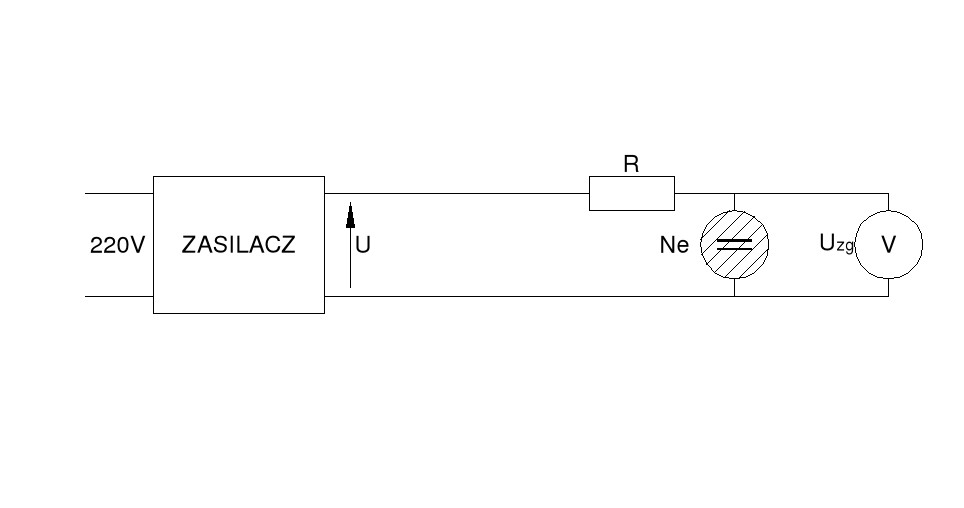
Druga część laboratorium polegała na badaniu drgań relaksacyjnych na podstawie dwu układów (rys 3 i 4). Należało zmierzyć tzw. napięcie zapłonu i gaśnięcia neonówki, która pełniła w obwodzie takiego „automatycznego klucza” rozładowującego kondensator po jego naładowaniu. Pomiary były wykonywane na układzie przedstawianym

przez rysunek 3 gdzie opór ma wartość 50 kΩ. Wartości tych napięć pochodzące 5 prób zebrane są w tabeli 3.

	1	2	3	4	5	średnia
Uz	75V	74,5V	74V	74V	73,5V	76V
Ug	62V	61,5V	59V	59V	58,5V	60V

Błąd systematyczny oporu wynosi ± 5%, więc jego wartością nominalną jest 2,5kΩ. Błąd systematyczny woltomierza wynosi ± 0,75V, co wynika z następującego wzoru (zakres:150V, klasa:0,5):

Czyli jest to błąd również napięcia zapłonu jak i gaśnięcia.

Drgania relaksacyjne bada się za pomocą układu przedstawionego na rysunku 4, gdzie opór początkowy ma 850kΩ ± 5% (± 42,5 kΩ), oraz kondensatora o pojemności 1μF ± 5% (± 5*10^-2μF) przy napięciu 87,5V. Ćwiczenie polegało na obliczeniu czasu 20 mrugnięć dla różnych oporów. Wyniki zestawione zostały w poniższej tabelce.

L.p.	R [kΩ]	ΔR [kΩ]	t [s]
1	850	± 42,5	21,80
2	722	± 36,1	18,70
3	570	28,5	14,46
4	560	± 28	14,08
5	470	± 23,5	12,85
6	380	± 19	10,62

Całkowity błąd pomiaru czasu liczony za pomocą średniego błędu kwadratowego wartości średniej (biorąc pod uwagę dość dużą niedokładność przy ręcznym mierzeniu czasu) przy stopniu ufności β=0,95 wynosi ± 4,3s. W związku z tym wyniki te mogą być miarodajne. Po podłączeniu do układu przedstawionego na rysunku 4 do zacisków neonówki oscyloskopu powstaje w przybliżeniu następujący obraz:

Rys. 1

Rys. 2

Rys. 3

Rys. 4

---