Imię i nazwisko: Setla Bartosz	Ćwiczenie nr M2 Wyznaczanie przyspieszenia ziemskiego przy pomocy wahadła rewersyjnego.
Kierunek i rok: Fizyka I rok	Ocena z kolokwium:	Ocena ze sprawozdania:	Ocena końcowa:
dr E. Jakubczyk

CZĘŚĆ TEORETYCZNA:

Wahadłem fizycznym nazywamy bryłę wykonującą drgania wokół osi nie przechodzącej przez środek ciężkości bryły.

1.Wahadło fizyczne

Wzór :

określa okres drgań wahadła fizycznego. Jeżeli wahadło zawiesimy w taki sposób, by jego oś była pozioma i wychylimy o mały kąt α z położenia równowagi, to wykonuje ona oscylacje. Ruch wahadła fizycznego dla małych wartości kąta α jest ruchem harmonicznym prostym.

Moment siły M dla wahadła wyraża się wzorem:

M = - mgd sin α

d - odległość środka ciężkości od punktu podparcia.

Ze względu na małą wartość kąta α moment siły możemy wyrazić wzorem:

M = - mgd α.

Moment kierujący wyrazi się wzorem:

D = mgd.

Z twierdzenia Steinera moment bezwładności możemy przedstawić równaniem:

I = I_S + md²

I_S - moment bezwładności względem osi przechodzącej przez środek ciężkości równoległej do osi oscylacji.

Podstawiają wzory na moment kierujący i moment bezwładności do równania:

otrzymamy następujący wzór na okres oscylacji:

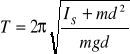
Znając okres oscylacji bryły o regularnych kształtach i znanej masie m, możemy obliczyć przyspieszenie ziemskie.

Wahadłem rewersyjnym nazywamy wahadło fizyczne o ustalonych osiach obrotu O i O'. Położenie środka ciężkości tego wahadła można zmieniać przez przesuwanie jednej z mas, gdy położenie drugiej jest ustalone.

2. Wahadło rewersyjne

Wprowadzając do wzoru na okres oscylacji wahadła fizycznego oznaczenie:

wyrazimy okres wahadła fizycznego wzorem:

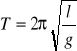
Tak więc okres drgań wahadła fizycznego wyrazi się takim samym wzorem jak okres drgań wahadła matematycznego o długości l. Wielkość l nazywamy długością zredukowaną wahadła fizycznego. Punkt O' leżący na prostej OS, odległy o l od punktu O nazywamy środkiem wahań wahadła fizycznego.

Jeśli wahadło zamocujemy w ten sposób, że będzie mogło wahać się wokół osi przechodzącej przez środek wahań O', to okres wyrazi się wzorem:

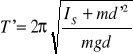
Pole grawitacyjne - własność przestrzeni, w której na umieszczone w nim ciało działa siła ciążenia: w pobliżu dowolnego ciała o masie M dowolny obiekt fizyczny doznaje przyspieszenia skierowanego ku środkowi masy ciała i proporcjonalnego do masy M.

Istotą grawitacji jest to, że dwie masy działają wzajemnie na siebie siłami. Grawitację możemy traktować jako bezpośrednie oddziaływanie między dwoma ciałami obdarzonymi masą. Taki punkt widzenia nazywa się koncepcją działania na odległość; ciała oddziałują nawet wtedy, gdy nie stykają się ze sobą.

Odmiennym punktem widzenia jest koncepcja pola, według której ciało obdarzone masą modyfikuje w pewien sposób otaczającą przestrzeń, tworząc tzw. pole grawitacyjne. Pole to działa następnie na każde znajdujące się w nim ciało obdarzone masą, wywierając nań siłę przyciągania grawitacyjnego.

Rozważmy Ziemię jako izolowaną masę. Jeżeli w pobliżu Ziemi umieścimy teraz ciało, będzie nań działać siła. W każdym punkcie przestrzeni siła ta ma określony kierunek i wartość. Kierunek jej jest radialny do środka Ziemi, wartość mg. Z każdym punktem w pobliżu Ziemi możemy stworzyć wektor g, który jest przyspieszeniem, jakiego doświadczyłoby ciało, gdyby zostało umieszczone w tym punkcie. Wektor g nazywamy natężeniem pola grawitacyjnego w tym punkcie. Ponieważ :

możemy zdefiniować natężenie pola grawitacyjnego w dowolnym punkcie, jako siłę grawitacji działającą w tym punkcie na jednostkę masy.

Zmiany przyspieszenia ziemskiego.

Przyspieszenie ziemskie g będzie zmieniać się wraz z wysokością, czyli z odległością od środka Ziemi. Obliczymy zmianę wartości g, jaka powstaje w miarę wzrostu odległości od powierzchni Ziemi. Z prawa powszechnego ciążenia:

po zróżniczkowaniu względem r otrzymujemy:

=>

Jednakże około połowa obserwowanej zmiany wartości g może być wyjaśniona za pomocą innego efektu, a mianowicie zmiany efektywnej wartości g wywołanej ruchem obrotowym Ziemi. Dla prędkości obrotowych, mniejszych o ich wartości krytycznej, g ma określoną, różną od zera wartość. Jest ona jednak mniejsza od wartości w tym samym punkcie na nie obracającej się Ziemi.

Na ciało działają następujące siły: pozorny ciężar ciała oraz siła przyciągania Ziemi. Ciało doznaje także przyspieszenia dośrodkowego a_R związanego z ruchem obrotowym Ziemi. Musi istnieć siła wypadkowa działająca na ciało w kierunku środka Ziemi. W wyniku siła przyciągania grawitacyjnego F (prawdziwy ciężar ciała) musi przewyższać pozorny ciężar ciała.

Z drugiej zasady dynamiki możemy zapisać:

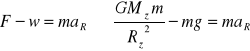
Taką wartość g otrzymalibyśmy wszędzie (zakładając kulisty kształt Ziemi), gdyby można było pominąć ruch obrotowy Ziemi.

W rzeczywistości, poza równikiem, przyspieszenie dośrodkowe nie jest skierowane do środka Ziemi. Sytuacja ekstremalna występuje na równiku. Tam:

.

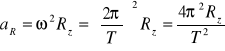
Wyznaczam okres drgań wahadła:

m - ilość okresów drgań,

T_m - czas trwania m drgań.

Wyznaczam średni okres drgań wahadła:

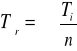
n - ilość pomiarów,

i - numer pomiaru.

Wyznaczam niepewność pomiaru okresu drgań wahadła:

Wyznaczam niepewność procentową:

Niepewność procentowa dla T₁:

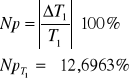
Niepewność procentowa dla T₂:

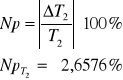
Tabela wyników pomiarów:

Numer pomiaru	h [cm]	10 T1 [s]	T1 [s]	T1śr [s]	10 T2 [s]	T2 [s]	T2śr [s]
1	4	11,580	1,1580	1,15785	13,500	1,3500	1,34990
2			11,577		1,1577			13,498	1,3498
1		6	10,934		1,0934	1,09335		13,393	1,3393	1,33955
2			10,933		1,0933			13,398	1,3398
1		8	10,576		1,0576	1,05765		13,291	1,3291	1,32925
2			10,577		1,0577			13,294	1,3294
1		10	10,393		1,0393	1,03955		13,193	1,3193	1,31995
2			10,398		1,0398			13,206	1,3206
1		12	10,336		1,0336	1,03365		13,103	1,3103	1,31045
2			10,337		1,0337			13,106	1,3106
1		14	10,368		1,0368	1,03685		13,025	1,3025	1,30255
2			10,369		1,0369			13,027	1,3027
1		16	10,464		1,0464	1,04640		12,959	1,2959	1,29585
2			10,464		1,0464			12,958	1,2958
1		18	10,605		1,0605	1,06055		12,903	1,2903	1,29040
2			10,606		1,0606			12,905	1,2905
1		20	10,788		1,0788	1,07890		12,876	1,2876	1,28800
2			10,790		1,0790			12,884	1,2884
1		22	10,991		1,0991	1,09915		12,827	1,2827	1,28280
2			10,992		1,0992			12,829	1,2829
1		24	11,214		1,1214	1,12125		12,812	1,2812	1,28120
2			11,211		1,1211			12,812	1,2812
1		26	11,449		1,1449	1,14480		12,811	1,2811	1,28110
2			11,447		1,1447			12,811	1,2811
1		28	11,688		1,1688	1,16895		12,832	1,2832	1,28310
2			11,691		1,1691			12,830	1,2830
1		30	11,948		1,1948	1,19470		12,861	1,2861	1,28615
2			11,946		1,1946			12,862	1,2862
1		32	12,194		1,2194	1,21955		12,912	1,2912	1,29120
2			12,197		1,2197			12,912	1,2912
1		34	12,449		1,2449	1,24510		12,991	1,2991	1,29915
2			12,453		1,2453			12,992	1,2992
1		36	12,711		1,2711	1,27130		13,082	1,3082	1,31005
2			12,715		1,2715			13,119	1,3119
1		38	12,968		1,2968	1,29690		13,225	1,3225	1,32160
2			12,970		1,2970			13,207	1,3207
1		40	13,234		1,3234	1,32345		13,358	1,3358	1,33590
2			13,235		1,3235			13,360	1,3360

Ponieważ w tabeli nie mieści się wartość, dla której okresy T₁ i T₂ są równe wartość tą odczytałam ze sporządzonego na podstawie wyników wykresu. Dlatego wartość obliczonego przeze mnie przyspieszenia jest bardzo przybliżona.

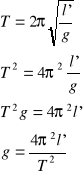
g - przyspieszenie ziemskie,

l' - długość zredukowana wahadła rewersyjnego,

T - okres drgań wahadła.

Długość zredukowana l' = 46 cm.

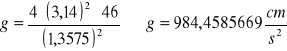
Niepewność przyspieszenia ziemskiego g obliczam metodą pochodnej logarytmicznej:

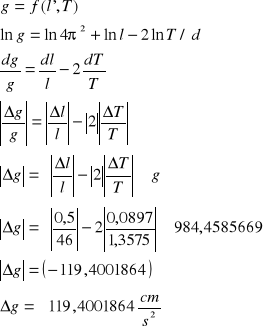
Obliczam niepewność procentową przyspieszenia ziemskiego g:

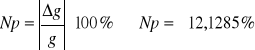
WNIOSKI:

Celem ćwiczenia było wyznaczenie przyspieszenia ziemskiego przy pomocy wahadła rewersyjnego. Podczas wykonywanie doświadczenia wystąpiły błędy: niedokładności przyrządów pomiarowych, niedokładność osoby przeprowadzającej pomiary. W przypadku wyznaczania przyspieszenia ziemskiego błąd jest znaczący +-12,1285% jednak mieść się w granicy błędu. W związku z powyższym mogę stwierdzić że powyższe doświadczenie wykonałem poprawnie.

---