Pracownia Zakładu Fizyki Technicznej Politechniki Lubelskiej
Nazwisko i imię studenta Krzysztof Kalinowski
|
Symbol grupy MD 103.5a |
||||||
Data wyk. Ćwiczenia
1996-11-15 |
Symbol ćwiczenia
3.1,3.2
|
Temat zadania Wyznaczanie charakterystyki licznika GM. Wyznaczanie czasu rozdzielczego licznika GM |
|||||
|
ZALICZENIE |
|
|
Ocena |
Data |
Podpis |
|
Własności jonizacyjne promieniowania jądrowego wykorzystuje się w detekcji tego promie-
niowania. Główne rodzaje detektorów to: detektory scyntylacyjne, półprzewodnikowe,
gazowe, iskrowe oraz liczniki Czerenkowa. Wśród detektorów gazowych wyróżniamy:
komorę jonizacyjną, licznik proporcjonalny, licznik Geigera-M*llera. Gazowy detektor
promieniowania składa się z dwu elektrod tworzących kondensator, umieszczony w
naczyniu wypełnionym gazem. Elektrody połączone są ze źródłem napięcia elektrycznego
oraz z urządzeniem rejestrującym.
Licznik GM jest najbardziej rozpowszechnionym detektorem promieniowania jądrowego. Zasadniczymi częściami licznika są: cylindryczna katoda i przeciągnięta wzdłuż jej osi
metalowa nić stanowiąca anodę. Elektrody zamknięte są w naczyniu wypełnionym gazem szlachetnym z dodatkiem gazu wieloatomowego. Jego zadaniem jest gaszenie impulsu lawinowego.
Rys.1. Schemat połączeń licznika GM
Liczba impulsów rejestrowanych przez licznik GM zależy od wartości napięcia doprowa-
dzonego do licznika. Krzywą przedstawiającą zależność liczby impulsów od napięcia zasilającego doprowadzonego do licznika w warunkach niezmiennego źródła pro-
mieniotwórczego i stałej czułości układu zliczającego, nazywa się charakterystyką licznika.
Czas rozdzielczy detektora definiuje się jako najmniejszy odstęp czasu między początkiem dwóch kolejnych zderzeń jonizujących, które powodują powstanie na wyjściu detektora dwóch odrębnych sygnałów.
Wykonanie ćwiczenia polega na zarejestrowaniu wyników pomiarów oraz dokonaniu obliczeń. Zestaw do badania licznika GM:
wyznaczanie charakterystyki licznika GM;
Ustalam:
- napięcie początkowe U=300 V
- skok napięcia 10 V
- czas trwania pojedynczego pomiaru 100 s
U |
N |
|
|
|
|
V |
- |
|
|
|
|
300 |
- |
380 |
38685 |
460 |
42856 |
310 |
32510 |
390 |
38829 |
470 |
43708 |
320 |
36271 |
400 |
39228 |
480 |
44219 |
330 |
36958 |
410 |
40312 |
490 |
44552 |
340 |
37720 |
420 |
40335 |
500 |
45397 |
350 |
37886 |
430 |
40838 |
510 |
46469 |
360 |
38372 |
440 |
41832 |
520 |
46601 |
370 |
38428 |
450 |
42199 |
530 |
47426 |
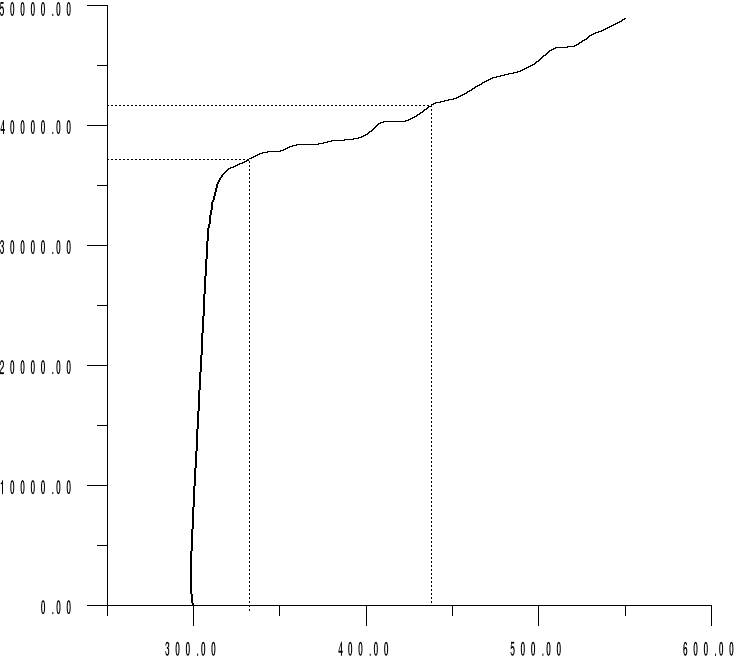
Charakterystykę napięciowo-zliczeniową licznika GM przedstawia rys.2.
Z zamieszczonych danych wynika, że:
- napięcie progowe wynosi Upr= 310
- napięcie robocze U = 382 V
Rys.2. Wyznaczona charakterystyka licznika GM
N [-]
Wyznaczanie nachylenia plateau metodą najmniejszych kwadratów.
W obszarze plateau zależność między U i N jest liniowa:
Ni = a Ui + b a,b - współczynniki
Lp. |
xi |
yi |
xi2 |
xiyi |
wi |
a |
b |
yi* |
Δyi* |
(Δyi*)2 |
1 |
400 |
392.28 |
160000 |
156912 |
1 |
|
|
393.06 |
-6.94 |
48.2 |
2 |
410 |
403.12 |
168100 |
165279 |
1 |
|
|
399.08 |
-10.92 |
119.2 |
3 |
420 |
403.35 |
176400 |
169407 |
1 |
|
|
405.1 |
-14.9 |
222 |
4 |
430 |
408.38 |
184900 |
175603 |
1 |
|
|
411.12 |
-18.88 |
356.4 |
5 |
440 |
418.32 |
193600 |
184061 |
1 |
|
|
417.14 |
-22.86 |
522.6 |
6 |
450 |
421.99 |
202500 |
189896 |
1 |
0.602 |
152.26 |
423.16 |
-26.84 |
720.4 |
7 |
460 |
428.56 |
211600 |
197138 |
1 |
|
|
429.18 |
-30.82 |
949.9 |
8 |
470 |
437.08 |
220900 |
205428 |
1 |
|
|
435.2 |
-34.8 |
1211 |
9 |
480 |
442.19 |
230400 |
212251 |
1 |
|
|
441.22 |
-38.78 |
1503.9 |
10 |
490 |
445.52 |
240100 |
218305 |
1 |
|
|
447.24 |
-42.76 |
1828.4 |
11 |
500 |
453.97 |
250000 |
226985 |
1 |
|
|
453.26 |
-46.74 |
2184.6 |
|
Σ |
Σ |
Σ |
Σ |
|
|
|
|
|
Σ |
|
4950 |
4654,7 |
2238500 |
2101264 |
|
|
|
|
|
9666.7 |
Otrzymałem równanie prostej: Ni = 0.602 Ui + 152.26
Ponieważ a = tg ϕ ,gdzie ϕ - kąt nachylenia plateau
tg ϕ = 0.602 ϕ = arctg 0.602 ϕ = 31.05°
Błędy jakimi obarczone są współczynniki a i b wynoszą:
Błąd nachylenia prostej: δtg ϕ = 0.5183 , czyli kąt ( 16.17 < ϕ < 42.43 )°
Wyznaczanie czasu rozdzielczego licznika GM:
Wyliczenie błędu metodą różniczkową:
t = 100 s
Korzystając z rozwinięcia funkcji w szereg otrzymuję błąd względny max:
Procentowo: σmax(τ)=0.382 ⋅ 100 % = 38.19 %
Δτm.= 0.382 ⋅ 2.365 ⋅ 10-5 = 9.03⋅ 10-6 s
( 1.462⋅10-5 < τ < 3.268⋅10-5 ) s
A
C
do układu
wzmacniającego
i rejestrującego
K
U
R
N2
U1
N1
U2
U [V]
Wyszukiwarka
Podobne podstrony:
4199
4199
praca-licencjacka-b7-4199, Dokumenty(8)
4199
obyna3.pl-4199 prace filozof w, Pedagogika, Filozofia
4199
4199
GE Cherokee 4199
więcej podobnych podstron