WfiTJ	1.Urszula Jeleń 2.Marcin Sikora		Rok 2	Grupa 2	Zespół: VII
Pracownia Fizyczna 2	Temat: Przerwa energetyczna w germanie.				Nr ćw. 122
Data wykonania: 27.10.1998	Data oddania: 17.11.1998	Zwrot do poprawy:	Data oddania:	Data zaliczenia:	OCENA:

Cel ćwiczenia

Wyznaczanie szerokości przerwy energetycznej przez pomiar zależności oporu monokryształu germanu.

Wprowadzenie

Półprzewodnik jest to materiał który w temperaturze bliskiej zera bezwzględnego zachowują się jak izolatory, natomiast w temperaturach wyższych mają opór pomiędzy metalami a izolatorami. Na wykresie poziomów energetycznych występuje przerwa energetyczna oddzielająca pasmo walencyjne od pasma przewodnictwa.

Półprzewodniki dzielą się na:

-półprzewodniki samoistne

-półprzewodniki domieszkowe z domieszką donorów, nazywane półprzewodnikami typu n

-półprzewodniki domieszkowe z domieszką akceptorów, nazywane półprzewodnikami typu p

-półprzewodniki domieszkowe typu mieszanego (p i n)

Półprzewodnikami samoistnymi nazywane są chemicznie czyste kryształy, takie jak german i krzem.

W temperaturze zera prądu elektrycznego, tworząc tzw. prąd dziurowy.

Liczbie elektronów w paśmie przewodnictwa półprzewodnika samoistnego jest równa liczba dziur w paśmie bezwzględnego pasmo walencyjne jest całkowicie zapełnione a pasmo przewodnictwa zupełnie puste. W temperaturach wyższych część elektronów z pasma walencyjnego przechodzi do pasma przewodnictwa, które częściowo zapełnione elektronami może przewodzić prąd elektronowy. Ponadto po przejściu elektronów z pasma przewodnictwa w paśmie tym pozostają puste miejsca, zwane dziurami, które również biorą udział w przewodzeniu przewodnictwa.

Wynikają stąd dwie cechy półprzewodników samoistnych:

-półprzewodnik samoistny w temperaturze zera bezwzględnego jest idealnym izolatorem

-przewodność elektryczna półprzewodnika samoistnego ma charakter aktywacyjny tzn. może być wywołana czynnikami takimi jak : temperatura, promieniowani, silne pole elektryczne, które są w stanie udzielić elektronowi energii większej od przerwy energetycznej.

Koncentracja nośników od w zależności od temperatury wyraża się wzorem:

n=p=const T^3/2 exp(-E_g/2kT)

Przewodność właściwa określona jest wzorem:

σ=enμ_n+epμ_p

gdzie e oznacza ładunek elementarny, μ_n i μ_p ruchliwość elektronów i dziur.

Przewodność zmienia się także pod wpływem zmiany liczby i ruchliwości nośników.

Spadek ruchliwości , spowodowany oddziaływaniem z drganiami sieci niemal kompensuje czynnik T^3/2. W rezultacie oporność opisać można czynnikiem wykładniczym:

R=const exp(E_g/2kT)

Lub

ln R=ln(const)+E_g/2kT

Skąd można obliczyć szerokość przerwy energetycznej.

Opracowanie wyników

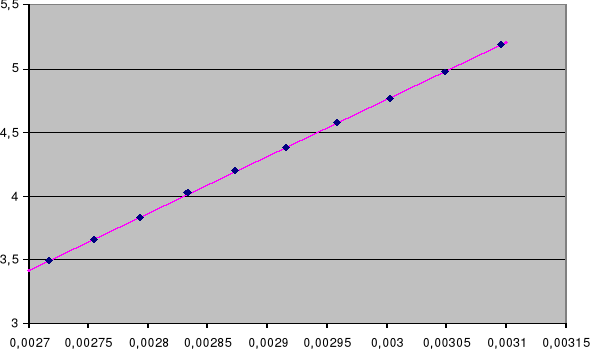
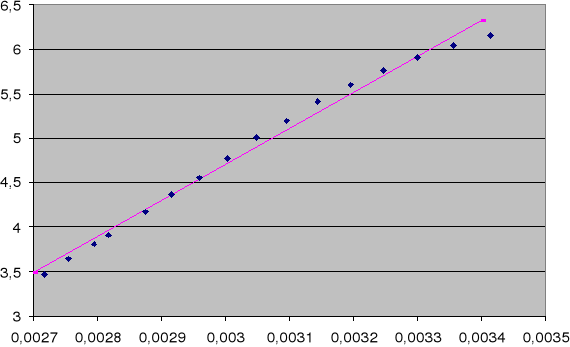
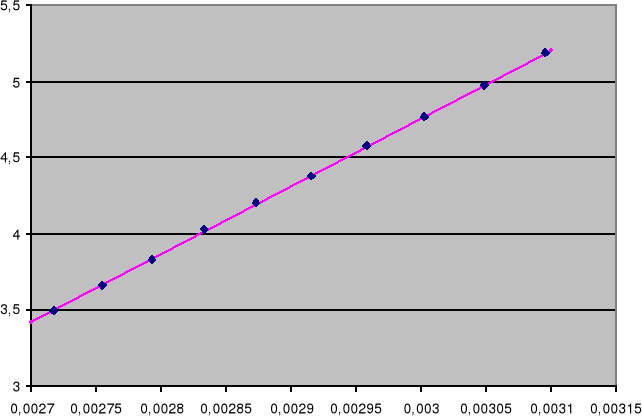
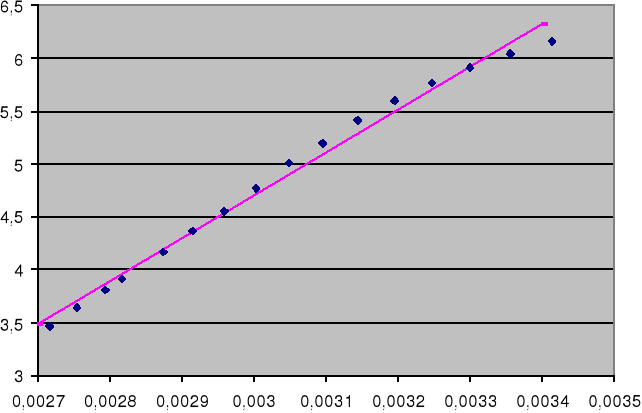
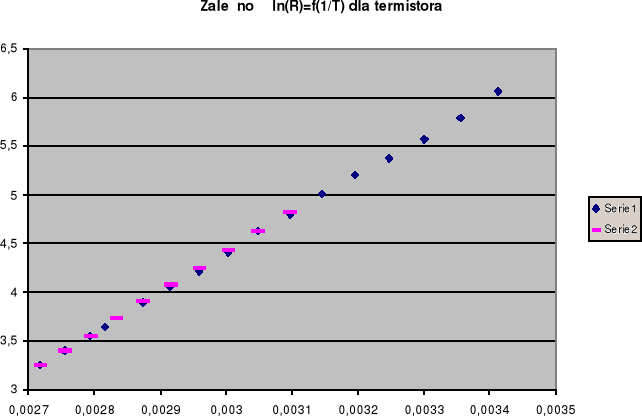
Załączone wykresy przedstawiają wykresy zależności ln(R) od 1/T wraz z linią regresji.. Pierwszy wykres dla podgrzewania,drugi dla studzenia próbki germanu. Metodą najmniejszych kwadratów obliczono współczynniki prostej wzdłuż której układają się punkty dla germanu. Nie odrzucono żadnych punktów.

Współczynniki te wynoszą:

dla temperatury rosnącej a=4056±114 ,błąd względny : 28%

b=-7,5±0,3 ,błąd względny : 4%

dla temperatury malejącej a=4463±54 ,błąd względny : 1,2%

b=-8,63±0,15 ,błąd względny : 1,7%

Wykorzystując wzór :

Obliczono :8

Dla temperatury wzrastającej:E_g=( 1,12 ± 0,03)*10^-19 [ J ] = ( 0,700 ± 0,02) [eV]

Dla temperatury malejącej: E_g=( 1,23 ± 0,014)*10^-19 [ J ] =( 0,770 ± 0,009) [eV]

Wykorzystując średnią ważoną otrzymano:

E_g= 0,75 [eV]

Wartość tablicowa wynosi E_gt=0,67[eV]

Różnica pomiędzy wartością doświadczalną i tablicową (E_gt-E_g)/E_gt wynosi:12%

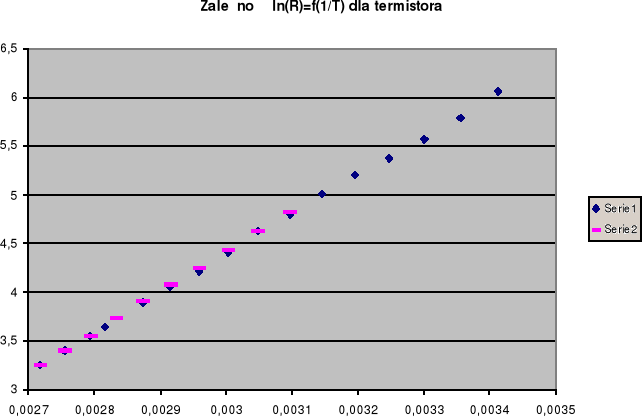
Wnioski:

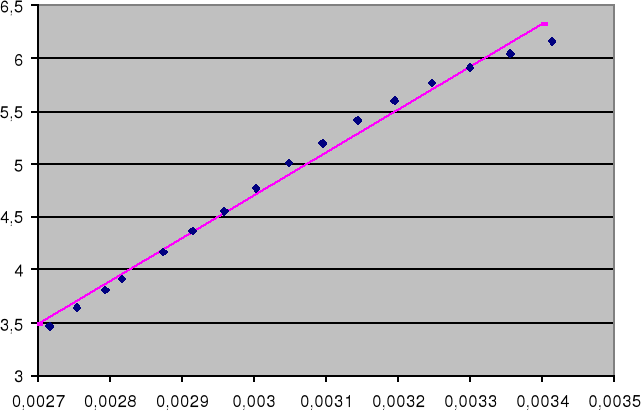
Błędy powstałe podczas wykonywania ćwiczenia i nie uwzględnione w dyskusji błędów mogły wyniknąć głównie z nierównomiernego nagrzewania się germanu, termistora i termometru .Co widać z otrzymanych błędów .Przy studzeniu zachodżące procesy miały bardziej qwazistatuczny charakter (niewielkie błędy). Zależność oporu termistora od temperatury ma charakter taki sam jak dla germanu, co może wskazywać że zbudowany jest on z półprzewodnika.

---