1. NAPÓR HYDROSTATYCZNY NA ŚCIANĘ PŁASKĄ
Na każdą powierzchnię ścianki naczynia lub zbiornika ciecz działa siłą o module p*dF, skierowana prostopadle do elementarnej powierzchni. Siły te, zwane elementarnymi naporami hydrostatycznymi, w ogólnym przypadku dowolnie ukształtowanej ścianki tworzą przestrzenny, dowolny układ sił, który redukuje się do wektora głównego oraz momentu ogólnego lub skrętnika. W wielu przypadkach praktycznych mamy do czynienia bądź to ze ściankami płaskimi, bądź to zakrzywionymi w ten sposób, że tworzą powierzchnie walcowe, kuliste lub stożkowe. Układ sił p*dF redukuje się wtedy do jednej wypadkowej, zwanej naporem hydrostatycznym. Weźmy pod uwagę figurę płaską o powierzchni F leżącą
w płaszczyźnie ścianki naczynia, nachylonej do poziomu pod
kątem ![]()
(jak na rysunku).
Na element powierzchniowy dF figury, którego środek leży w odległości „z" działa napór elementarny ![]()
. Dla całej figury otrzymamy układ sił przestrzenny równoległy, a jego wypadkowa określona jest całką powierzchni figury
![]()
Całka ta przedstawia moment statyczny figury F względem
płaszczyzny O-O i jako taka równa się Fzs, gdzie
zs jest współrzędną ciężkości figury. Zatem
![]()
Iloczyn ![]()
określa ciśnienie całkowite, jakie panuje
w środku ciężkości figury F.
Napór cieczy na płaską figurę dowolnie zorientowaną równa się ciśnieniu całkowitemu w środku ciężkości figury pomnożonemu przez pole powierzchni tej figury.
Gdy pn=0 (gdy na powierzchni zwierciadła cieczy jest takie
samo ciśnienie jak na zewnętrznej stronie ścianki -
w szczególności może to być ciśnienie atmosferyczne) to przez
wartość zs należy rozumieć głębokość zanurzenia środka
ciężkości.
2. ŚRODEK NAPORU
Cechy wektora siły naporu:
1. Wartości (moduł) ![]()
2. Kierunek działania - prostopadły do płaszczyzny ściany
naczynia
3. Punkt zaczepienia - środek naporu (punkt D)
Dla figury usytuowanej poziomo (np. w dnie naczynia), środek
naporu pokrywa się ze środkiem ciężkości figury. Jednakże
w przypadku ściany pochyłej tak nie jest.
Moment siły wypadkowej układu sił względem dowolnej osi równa się sumie momentów poszczególnych sił względem tej osi (twierdzenie z mechaniki).
Mw=M1+M2+...
Dla sił działających na figurę F oraz osi Ox twierdzenie to
można zapisać w postaci:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Porównując prawe strony równań (a) i (b) otrzymujemy:
![]()
![]()
Odległość środka naporu od osi Ox równa się ilorazowi
![]()
![]()
- nie zależny od ![]()
Środek naporu położony jest zawsze poniżej środka ciężkości
figury.
Twierdzenie Steinera dla rozpatrywanej figury ma postać:
![]()
![]()
- powierzchniowy moment bezwładności figury względem
prostej przechodzącej przez środek ciężkości figury, równoległej do osi Ox
![]()
![]()
- promień bezwładności figury.
Moment statyczny figury
Sx=Fys
Podstawiając powyższe zależności do równania
![]()
otrzymuje się
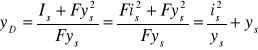
ponieważ 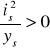
to yD>ys.
Odległość środka naporu od środka ciężkości figury mierzona
w płaszczyźnie figury wynosi
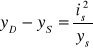
.
Między współrzędnymi z i y zachodzi zależność
![]()
,
i analogicznie
![]()
![]()
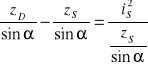
Po przekształceniu otrzymujemy
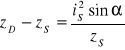
![]()
Z powyższego równania wynika, że im bardziej ściana jest
nachylona do poziomu tym bardziej środek naporu oddala się od środka ciężkości figury. Odległość ta jest największa dla ściany pionowej. Gdy figura ma oś symetrii równoległą do osi Oy wówczas dla wyznaczenia położenia środka naporu wystarczy obliczyć tylko współrzędne yD. W przypadku figury niesymetrycznej należy również wyznaczyć współrzędną xD.
NAPÓR NA ŚCIANĘ ZAKRZYWIONĄ
Zamknięty zbiornik z cieczą o ciężarze właściwym ![]()
pod
ciśnieniem pn posiada dowolnie zakrzywione ściany. Układ
współrzędnych przyjęto w ten sposób, że osie Ox i Oy znajdują
się w płaszczyźnie O-O a oś Oz jest skierowana
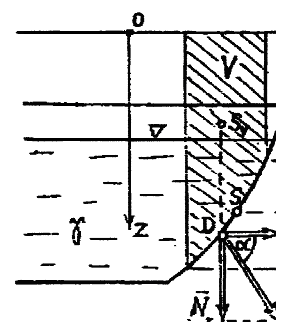
pionowo w dół. Na rysunku poniżej przedstawiono płat
powierzchni zakrzywionej oraz jego rzuty Fx, Fy, Fz na płaszczyzny układu współrzędnych.
Wektor dF elementarnej powierzchni płata ma składową dFx,
dFy, dFz, które reprezentują pola rzutów elementarnej
powierzchni dF na odpowiednie płaszczyzny układu.
Działanie cieczy na powierzchnię dF jest elementarnym
naporem hydrostatycznym
![]()
Składowe poziome elementarnego naporu hydrostatycznego
![]()
![]()
gdzie:
![]()
- ciężar właściwy cieczy
z- głębokość zanurzenia elementarnych powierzchni dFx, dFy
Składowe poziome dla całych powierzchni wynoszą![]()
![]()
![]()
![]()
gdzie:
zs - głębokość zanurzenia środków ciężkości figur Fx, Fy
(punkty sx i sy są rzutami środka ciężkości s na odpowiednie płaszczyzny pionowe). Uogólniając powyższe można napisać
![]()
gdzie:
Nn - składowa pozioma naporu na powierzchnię zakrzywioną
zs - głębokość zanurzenia środka ciężkości rzutu powierzchni zakrzywionej na płaszczyznę pionową…………………………….
Fn - pole powierzchni rzutu na płaszczyznę pionową
Twierdzenie
Składowa pozioma naporu cieczy na powierzchnię zakrzywioną obliczana w dowolnym kierunku jest równa naporowi na figurę płaską uzyskaną przez zrzutowanie powierzchni zakrzywionej na płaszczyznę pionową prostopadłą do tego kierunku.
Napór elementarny w kierunku Oz wynosi:
![]()
Iloczyn zdFz związany jest z objętością słupa cieczy.
Natomiast ![]()
objętością bryły cieczy ograniczonej
od dołu powierzchnią zakrzywioną, a od góry powierzchnią
O-O.
![]()
Składowa pionowa naporu cieczy na powierzchnię zakrzywioną równa się ciężarowi bryły cieczy ograniczonej od dołu tą powierzchnią a od góry powierzchnią O-O.
Jeśli pn=0 to płaszczyzna O-O pokrywa się
z płaszczyzną cieczy. Wektor siły Nz skierowany jest pionowo ku powierzchni zakrzywionej od strony zwilżonej a jego linia działania przechodzi przez środek ciężkości bryły określonej powyżej. Linie działania sił Nh i Nz w ogólnym przypadku powierzchni nie przecinają się w jednym punkcie, a więc są to siły skośne. Wtedy działanie cieczy na powierzchnię
zakrzywioną nie sprowadza się do jednej wypadkowej, lecz do
skrętnika. Natomiast, gdy powierzchnia zakrzywiona ma pionową płaszczyznę symetrii lub, gdy jest powierzchnią walcową o tworzącej poziomej, wtedy przestrzenny układ sił złożony z naporów elementarnych redukuje się do jednej wypadkowej, zwanej naporem hydrostatycznym.
![]()
![]()
Składową poziomą i pionową wyliczamy z wyżej wymienionych
wzorów, a jego kierunek pochylenia ze wzorów:
![]()
![]()
Środek naporu wyznacza się jako punkt przecięcia linii działania
wektorów Nh i Nz. W przypadku powierzchni nieregularnie
zakrzywionej punkt ten nie leży na samej powierzchni, lecz
poza nią.
Wyszukiwarka
Podobne podstrony:
wzor, Studia, Mp - Mechanika płynów
egzamin z dnia 9, Studia, AAAASEMIII, 3. semestr, Mechanika Płynów I, MP I
Mechanika płynów - Wykład 1, Studia, ZiIP, SEMESTR VI, Mechanika płynów (MP)
1 Równania Ciągłości, Studia, Mp - Mechanika płynów
Mechanika pynw, Studia, Mp - Mechanika płynów
sciaga MP, INŻYNIERIA ŚRODOWISKA WGGiIŚ AGH inżynierskie, SEMESTR 3, Mechanika Płynów
wyznaczanie współczynnika strat liniowych, studia, V semestr, Mechanika płynów
Newton jest jak Herkules z bajki, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
PLYNY4~1, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
Podstawowe charakterystyki temperatury powietrza, Księgozbiór, Studia, Mechanika Płynów i Dynamika G
ruch laminarny2, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
POLITE~2, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
PLYNY44, Księgozbiór, Studia, Mechanika Płynów i Dynamika Gazów
mp-grC, pwr, W7 wydział inżynierii środowiska, Pwr OŚ Ochrona Środowiska, Semestr 2, mechanika płynó
Kopia 4.17, mp 4.17, POLITECHNIKA WROCŁAWSKA INSTYTUT TECHNIKI CIEPLNEJ I MECHANIKI PŁYNÓW
więcej podobnych podstron