Ćwiczenia nr 3/ zastosowanie ciągów/
1)Pensja pracownika w pewnym roku zatrudnienia wynosi 1000zł, przy czym po każdym roku zatrudnienia ma wzrosnąć o 40zł. Kiedy pensja przekroczy 1400zł?
2)Ile będzie wynosiła łączna pensja pracownika z poprzedniego przykładu za n = 11 lat (zakładamy, że na początku każdego roku wzrasta o 40 zł)?
3)W pewnym zakładzie obroty w 2002r wynosiły 200 000zł i rocznie wzrastają o ![]()
. Jakie będą obroty w 2011 roku?
4)Jaką kwotę należy złożyć w banku, by po 10 latach mieć kwotę 6000 zł (oprocentowanie proste na r=10% rocznie).
5)Dokonujemy zakupu towaru w fabryce za 200 000 zł. Firma proponuje nam następujący system sprzedaży: przy płatności natychmiast otrzymujemy 3% rabatu, w przeciwnym wypadku termin płatności wynosi 2 miesiące.
Będę dysponował gotówką za 2 miesiące, więc rozważam wzięcie kredytu komercyjnego oprocentowanego 1% miesięcznie. Czy warto?
6)Chcemy dokonać lokaty kapitału. Mamy możliwość wyboru jednego z dwóch banków A oraz B. Ich oferta jest następująca:
Bank A - kapitalizacja z dołu, r = 11%, Bank B - kapitalizacja z góry, r = 10%. Który Bank wybrać?
7)W pewnym banku ROR-y były oprocentowane 8% przy miesięcznej kapitalizacji odsetek, następnie obniżono oprocentowanie na 3%, a kapitalizację zmieniono na roczną. O ile pogorszono warunki?
8) W banku A i B z takiego samego kapitału uzyskano po 2,5 latach taką samą wartość. W banku A kapitalizacja była półroczna z nominalną stopą procentową 12%. W banku B kapitalizacja była ciągła. Wyznacz nominalną stopę procentową dla banku B. Który bank w perspektywie 3 lat oferuje korzystniejsze warunki?
9) Na jaki procent należy złożyć kapitał, aby przy ciągłej kapitalizacji odsetek potroił on swoją wartość po 10 latach
10) Jaki był kapitał początkowy, jeżeli po 4 latach przy nominalnej stopie procentowej 9% i kwartalnej kapitalizacji odsetek z góry wzrósł on do kwoty 15.000 zł.
11) Jaki był kapitał początkowy, jeżeli po 3 latach przy nominalnej stopie procentowej 9% i ciągłej kapitalizacji odsetek wzrósł on do kwoty 10.000 zł?
I Kapitalizacja odsetek
Oznaczenia, jakie stosujemy:
![]()
-kapitał początkowy
![]()
stopa procentowa
![]()
-okres kapitalizacji odsetek
1)Kapitalizacja prosta
![]()
2)Kapitalizacja złożona z góry ![]()
3)Kapitalizacja złożona z dołu
![]()
4) Kapitalizacja ciągła
![]()
Jeżeli kapitalizacja odsetek następuje w podokresach, wówczas nasze wzory przyjmą następujące postaci:
1)Kapitalizacja prosta ![]()
2)Kapitalizacja złożona z góry 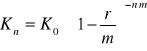
3)Kapitalizacja złożona z dołu 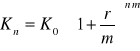
4) Kapitalizacja ciągła
![]()
![]()
- kapitał końcowy
![]()
- czas trwania lokaty w latach
Rozwiązania:
Ad. 1)
a1 = 1000 r = 40
a2 = 1000 + 40 itd.
an = 1400 = 1000 + (n-1)⋅40
stąd
![]()
n = 11
zatem dla n > 11 pensja przekroczy 1400zł.
Ad.2)
a1 = 1000⋅12 = 12000 zł (łączna pensja za pierwszy rok pracy),
a2 = 1040⋅12 = 12000 zł + 480 zł (łączna pensja za drugi rok pracy),
a3 = 1080⋅12 = 12000zł + 2⋅480zł (łączna pensja za trzeci rok pracy).
Mamy więc do czynienia z ciągiem arytmetycznym, w którym:
a1 = 12000zł r = 480zł
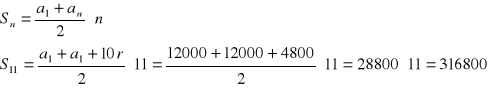
Ad.3)
a1 = 200000 zł. = O02
a2 = 200000 + 0,02 ⋅ 200000 = 1,02 ⋅200 000 =O03
. . . . . . . . .. . . .. . .. . . . .. . .. .. . .. .. . . . .. . . .. . . ..
a9 = a1 ⋅ 1,028 = 234 330 zł, czyli obroty w 2011 roku wyniosą 234330 zł (przy zachowaniu stałego tempa wzrostu).
Ad. 4)
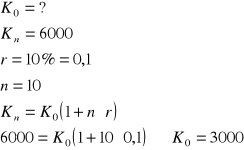
![]()
Ad.5)
zapłata za 2 miesiące - 200 000 zł
zapłata z wykorzystaniem kredytu:
zaciągam kredyt na kwotę
200 000 zł - 0,03·200 000 zł = 200 000 zł - 6 000 zł = 194 000 zł
po dwóch miesiącach spłacam
194 000(1 + 0,01)2 = 197 889,40 zł
Wniosek:
Warto wziąć kredyt i zapłacić natychmiast, chociaż różnica jest nieznaczna
Ad. 6)
Bank A - kapitalizacja z dołu, r = 11%, Kn = K0⋅(1 + 0,11)n
Bank B - kapitalizacja z góry, r = 10%, Wn = K0⋅(1 - 0,1)-n
Który bank wybrać?
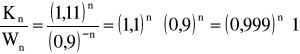
stąd : B oferuje nieznacznie lepsze warunki, mimo iż nominalnie jego oprocentowanie jest gorsze o jeden punkt procentowy.
Ad. 7)
Efektywna stopa procentowa odpowiadająca stopie oprocentowania składanego, to roczna stopa procentowa z rocznym okresem kapitalizacji odsetek równoważna danej stopie.
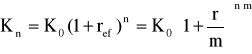
stąd 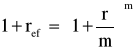
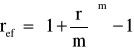
Rozwiązanie zadania nr7:
Po obniżeniu oprocentowania mamy wzór na wartość przyszłą:
Kn = K0(1 + 0,03)n
r = 3% jest oprocentowaniem efektywnym rachunku. Według wcześniejszych warunków wartość przyszłą należało wyznaczyć zgodnie ze wzorem:
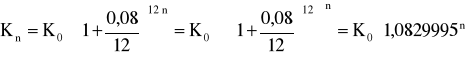
.
1,0829995 = 1 + ref
ref = (1,0067)12 - 1 = 1,0829995 - 1 ≈ 8,3%
ref - 3% = 5,3 p.p. - o tyle pogorszono warunki oprocentowania
Ad.8)
LOGARYTMY
![]()
≡ ay = x, a > 0, a ≠ 1, x > 0
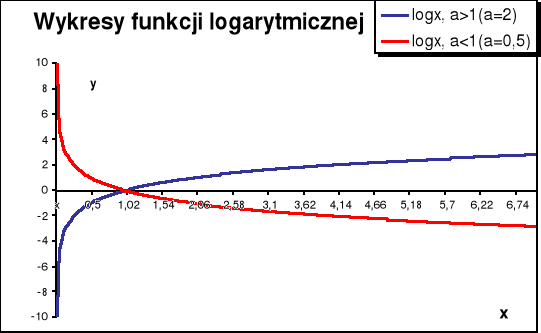
Przykład :
log10100 = 2 ≡ 102 = 100,
log2![]()
≡ 2-4 = ![]()
Przykład :
Rozwiązać równanie
(1,02)n-1 = 2
Mamy (n-1)log 1,02 = log 2
stąd n-1 = 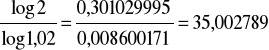
Własności:
loga1 = 0
logaa = 1
loga(xy) = logax + logay
loga![]()
= logax - logay
loga(xn) = n logax
logax = ![]()
,
oznaczenia: log10x = log x
logex = ln x
Uwaga:
log x = M ln x gdzie M = log10e = ![]()
Rozwiązanie zadania nr 8.
Z tego samego kapitału po 2,5 latach otrzymano w obydwu bankach taką samą wartość więc zachodzi równość:
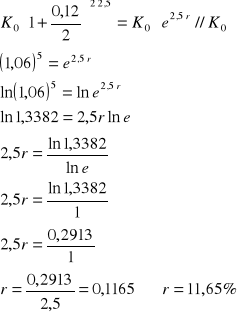
Zatem w banku B obowiązywała stopa procentowa na poziomie 11,65%
Który bank w perspektywie 3 lat oferuje korzystniejsze warunki?
A: 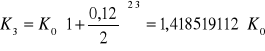
B: ![]()
Zatem w perspektywie 3 lat bank A oferuje lepsze warunki.
Ad.9)
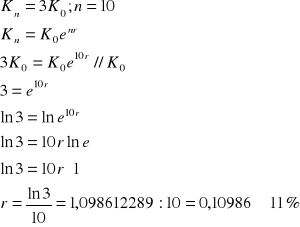
Ad.10)
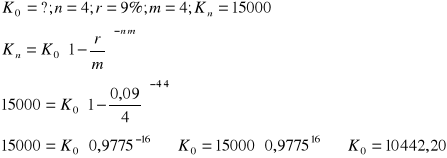
Ad. 11)
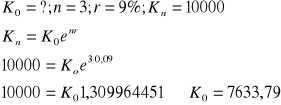
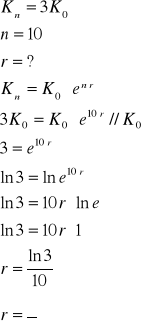
Wyszukiwarka
Podobne podstrony:
EGZAMIN Z MATEMATYKI, WSFiZ rok 1
Egzamin z rachunkowsci finansowej gr II, WSFiZ rok 1
Konsument i producent budżet, WSFiZ rok 1
PRODUCENT, WSFiZ rok 1
Egzamin poprawkowy ekonometria3, WSFiZ rok 2, Ekonometria
Rachunkowosc egzamin gr. I, WSFiZ rok 1
Kolokwium z matematyki, WSFiZ rok 1
TRENING PRZED KOLOKWIUM, WSFiZ rok 1
Kolokwium z matematyki na zarzdzaniu dzienne, WSFiZ rok 1
w-pochodne, WSFiZ rok 1
OPŁACALNOŚĆ i pieniądz, WSFiZ rok 1
Zawartość merytoryczna kont kosztów rodzajowych w skrócona, WSFiZ rok 1
Egzamin z matematykiImi i nazwisko3, WSFiZ rok 1
EGZAMIN Z MATEMATYKI, WSFiZ rok 1
Egzamin z rachunkowsci finansowej gr II, WSFiZ rok 1
Statystyka kolos 3[1], Psychologia Wsfiz II rok
Tematy-1 rok- WSFiZ w Warszawie 2010, 30 tematów
MOJE NOTATKI 2009 ROK, wsfiz
Zadania domowe statystyka, Psychologia Wsfiz II rok
więcej podobnych podstron