WSTĘP TEORETYCZNY

1. PODSTAWOWE ZAŁOŻENIA TEORII KINETYCZNO-MOLEKULARNEJ DLA GAZÓW.

Podstawy teorii molekularno-kinetycznej zostały sformułowane już w Grecji. Demokryt i Leukippos (VI - V w p.n.e.) twierdzili, że wszystkie ciała składają się z maleńkich, niewidocznych cząstek, ziaren. Im zawdzięczamy ideę atomistycznej budowy materii. Podstawy współczesnej teorii molekularno-kinetycznej sformułowano w wieku ubiegłym. Jej twórcami są: J. Joule, R. Clausius, później C. Maxwell, L. Boltzmann oraz fizyk polski M. Smoluchowski.

Podstawowymi doświadczalnymi dowodami prawdziwości teorii molekularno-kinetycznej są zjawiska: dyfuzja w gazach, cieczach i ciałach stałych, ruchy Brown`a w cieczach i gazach.

Odpowiadając na pytanie, jakie są główne założenia teorii molekularno-kinetycznej moglibyśmy wymienić następujące:

- Ciało ma strukturę ziarnistą, jest zbudowane z cząstek, atomów. Liczba cząstek (atomów) składających się na ciało jest ogromna.

- Cząsteczki tworzące dane ciało wykonują bezładne ruchy zwane ruchami cieplnymi (termicznymi). Zależą one od oddziaływań wzajemnych cząstek i zmieniają się przy zmianie stanu skupienia danego ciała (inny jest charakter tego ruchu w gazach, a jeszcze inny w cieczach i ciałach stałych).

- Średnia prędkość cząstek zależy od temperatury ciała T, gdzie T jest tzw. temperaturą bezwzględną (czyli liczoną w skali bezwzględnej).

- Całkowitą energię ciała w teorii molekularno-kinetycznej możemy przedstawić jako sumę energii:

gdzie:

E_k - energia kinetyczna ciała jako całości w ruchu makroskopowym,

E_p - energia potencjalna całego ciała w pewnym zewnętrznym polu sił np.

elektrycznym, grawitacyjnym.

U - tzw. energia wewnętrzna ciała związana z cieplnym ruchem cząstek i ich

oddziaływaniem.

2. PRZEMIANY GAZOWE.PRAWA I PRACE W KAZDEJ Z PRZEMIAN

• Przemiana izotermiczna (
  )

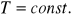
Prawo Boyle`a-Mariotta. Zależność między parametrami wynika z równania gazu doskonałego i nosi nazwę prawa Boyle`a-Mariotta:

czyli

Iloczyn ciśnienia i objętości gazu jest wielkością stałą.

W procesie izotermicznym gęstość gazu jest wprost proporcjonalna do ciśnienia. We współrzędnych p,V wykresem przemiany izotermicznej jest hiperbola.

gdzie

T₁

T₂

T₃

Praca przemiany izotermicznej gazu doskonałego.

Praca

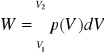
, podstawiając
mamy:

Ciepło przemiany wyznaczamy stosując I zasadę termodynamiki:

Energia wewnętrzna U gazu doskonałego podczas przemiany izotermicznej nie ulega zmianie. Gdy gaz sprężamy od ciśnienia p₁ do p₂, zmieniając jego objętość V₁ na V₂, wykonujemy pracę mechaniczną W, przekazując energię do otoczenia w postaci ciepła, za pośrednictwem sprężanego gazu (
).

• Przemiana izobaryczna (
  )

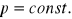
Prawo Gay-Lussaca. Zależność między parametrami dla stanu pierwszego i drugiego podczas przemiany izobarycznej w tym przypadku jest następująca:

lub
nosi ona nazwę prawa Gay-Lussaca.

Zależność tę można wypowiedzieć następująco: pod stałym ciśnieniem objętość określonej ilości gazu doskonałego jest wprost proporcjonalna do jego temp. bezwzględnej.

p=const. p=const. Wykresy przemiany izobarycznej

gazu doskonałego.

T₁ T₂ V₁ V₂

Praca przemiany: Zgodnie ze wzorem na pracę: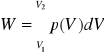
oraz uwzględniając, że
mamy

a dla gazu doskonałego:

• Przemiana izochoryczna. (
  )

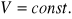
Prawo Charlesa: Zależność między parametrami w stanie pierwszym i drugim ma w tym przypadku postać:
lub

co oznacza, że w procesie izochorycznym ciśnienie gazu doskonałego jest wprost proporcjonalne do temperatury.

Wykres tej przemiany przedstawiono we współrzędnych V,T i T,p.

V T

izochora izochora

T p

Praca przemiany: Ponieważ
, a więc praca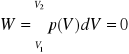

• Przemiana adiabatyczna (bez przepływu energii w postaci ciepła *Q=0)

Podczas adiabatycznego rozprężania gaz wykonuje pracę przeciwko siłom zewnętrznym kosztem swej energii wewnętrznej. Przy adiabatycznym sprężaniu energia wewnętrzna gazu rośnie kosztem pracy zewnętrznej. Zatem przy adiabatycznym rozprężaniu temp. maleje, a przy adiabatycznym sprężaniu temp. rośnie.

Praca przemiany: Z I prawa termodynamiki mamy
podstawiając
otrzymujemy
, a dla gazu doskonałego

lub

p adiabata

Wykres przemiany adiabatycznej gazu doskonałego.

izoterma

V

3. CIEPŁO WŁAŚCIWE.

Podczas ogrzewania gazu mogą ulegać zmianie wszystkie jego parametry, można go również ogrzewać w stałej objętości (przemiana izochoryczna) lub pod stałym ciśnieniem (przemiana izobaryczna). W każdym z tych przypadków 1 mol gazu ogrzewając o 1K pobierze określoną ilość energii. Wiemy, że związek miedzy dQ i dT zależy od rodzaju przemiany, w szczególności w procesie adiabatycznym dQ=0 dla dT0, więc c_adiab.=0 oraz w dwu typach procesów, które mają duże znaczenie w termodynamice :

• izochorycznym (c_v-ciepło właściwe przy stałej objętości)
  

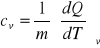
• izobarycznym (c_p- ciepło właściwe przy stałym ciśnieniu)
  

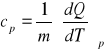
4. RÓŻNICE WARTOŚCI Cp , Cv I Cp/Cv DLA GAZÓW O RÓŻNYCH STOPNIACH SWOBODY.

Ciepło molowe w przemianie izobarycznej (c_p) jest większe niż ciepło molowe w przemianie izochorycznej (c_v), ponieważ przy ogrzewaniu gazu w stałej objętości całe dostarczane ciepło jest zużywane wyłącznie na podniesienie jego temperatury, natomiast w stałym ciśnieniu część dostarczanego ciepła zostaje zużyta na wykonanie pracy (przesunięcie tłoka w celu zachowania stałego ciśnienia) i tylko część na podwyższenie temp. c_pc_v . Dla gazu doskonałego zachodzi zależność: c_p-c_v=R , gdzie R- stała gazowa (R=8,31
) ponieważ dla gazu doskonałego ciepła molowe wynoszą odpowiednio c_p=2,5R i c_v=1,5R , więc c_p-c_v=R

Stosunek c_p/c_v wykazuje ciekawe prawidłowości. Dla gazów jednoatomowych jest on równy 1,67 , dla dwuatomowych 1,4 , a dla trzyatomowych 1,4 i nosi nazwę współczynnika Poissona χ=c_p/c_v

Dla gazu doskonałego χ=1,67. Stosunek ten dla danego gazu decyduje o przebiegu przemiany adiabatycznej.

5. WYPROWADZENIE WZORU.

Przypuśćmy, że w zbiorniku zaopatrzonym w ruchomy tłok znajduje się jeden kilomol gazu. Ciepło
potrzebne do ogrzania tego gazu
przy stałym ciśnieniu wynosi:
. Korzystając z tego związku oraz ze związków
i
pierwszą zasadę termodynamiki
możemy zapisać w postaci
. Różniczkując równanie stanu gazu
dla procesu izobarycznego (
), otrzymujemy
. Po podstawieniu tej zależności do poprzedniego związku mamy
stąd, po uproszczeniu przez
, dostajemy
.Według wzorów
i
molowe ciepło właściwe gazu w stałej objętości
. Zgodnie ze wzorem
molowe ciepło właściwe gazu przy stałym ciśnieniu jest zatem równe
a stosunek
wynosi

.

6. UKŁAD POMIAROWY.

7. TABELA POMIARÓW.

h1 [cm]	h2 [cm]	h1-h2 [cm]
54,6 60,5 58,9 63 58,9 62,7 58 58,3 55 62,2	9,1 9,8 6,5 9,3 7,3 9,2 8,5 9,7 8,7 7,7	45,5 50,7 52,4 53,7 51,6 53,5 49,5 48,6 46,3 54,5	1,2 1,19329 1,12405 1,17318 1,14147 1,17196 1,17172 1,19959 1,18790 1,14128

8. OPRACOWANIE WYNIKÓW.

Na podstawie otrzymanych wyników obliczamy stosunek c_p/c_v ze wzoru:
=
.

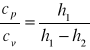
Np. dla pierwszego pomiaru otrzymujemy:
=

Wartość średnia tego stosunku dla wszystkich pomiarów wynosi:
_i=

Błędy pomiarowe obliczamy metodą Gaussa.

Obliczamy błędy poszczególnych pomiarów ze wzoru:

np. dla pierwszego pomiaru

Lp.
1 2 3 4 5 6 7 8 9 10	1,2 1,19329 1,12405 1,17318 1,14147 1,17196 1,17172 1,19959 1,18790 1,14128	0,02956 0,02285 0,04639 0,00274 0,02897 0,00152 0,00128 0,02915 0,01746 0,02916

Obliczamy sumę kwadratów błędów poszczególnych pomiarów:

Obliczamy średni błąd kwadratowy wartości średniej: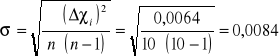

Ostateczny wynik stosunku c_p/c_v podajemy w postaci:
czyli
- jest to najbardziej prawdopodobny wynik serii pomiarów.

Metoda doświadczalna znajdowania .

W dużym naczyniu szklanym N o objętości kilkudziesięciu litrów zawarty jest badany gaz , znajdujący się pod ciśnieniem p niewiele wyższym od ciśnienia atmosferycznego . Gaz zamknięty jest kurkiem , który w pewnej chwili otwieramy i zamykamy ponownie z chwilą wyrównania się ciśnienia z ciśnieniem atmosferycznym . Powietrze rozpręża się , przy czym można przyjąć , że rozprężenie to zachodzi adiabatycznie .Ulega ono przy tym oziębieniu . Po pewnym czasie dzięki wymianie z otoczeniem temperatura powietrza pozostałego w naczyniu zrówna się z temp. otoczenia i wskutek ogrzania, ciśnienie gazu podniesie się . Wytworzy się więc nadwyżka ciśnienia , tym razem mniejsza od nadwyżki początkowej.

Niech początkowa nadwyżka równa się p₁ . Wypuszczenie gazu na zewnątrz odpowiada rozprężeniu o V , rozprężeniu temu odpowiada spadek ciśnienia

Przypuśćmy , że po wyrównaniu się temperatur nadwyżka ciśnienia wynosi p₂ . W porównaniu z ciśnieniem początkowym nastąpił spadek o
, ale ten sam spadek otrzymaliśmy rozprężając gaz izotermicznie o tę samą V zatem:
. Ze wzoru na adiabatę:

Z izotermy
. Porównując stronami otrzymujemy: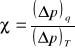
. Ponieważ w obu przypadkach mamy te same wartości p i V to:

9. UWAGI I SPOSTRZERZENIA.

Błąd w głównej mierze spowodowany jest mylnymi odczytami wysokości słupa wody oraz nieszczelnością układu pomiarowego ( w założeniu przemiana adiabatyczna zachodzi bez wymiany ciepła z otoczeniem ).

Niepewność odczytu wynika ze skończonej wartości grubości podziałki na przyrządzie pomiarowym (miara krawiecka) oraz z przyciągania międzycząsteczkowego , które powstaje na powierzchni cieczy(menisk) . Niemożliwe więc było jednoznaczne ( w każdym z 10 pomiarów ) określenie wysokości słupa wody, co spowodowało powstanie błędów w przeprowadzonych pomiarach.

Porównanie otrzymanego wyniku z wartością tablicową.

Cząstki jednoatomowe mają trzy stopnie swobody , odpowiadające trzem wzajemnie prostopadłym translacjom x, y, z , a więc dla gazów jednoatomowych : = 5/3 = 1,67

Cząstki dwuatomowe mogą ponadto wykonywać obroty wokół dwóch wzajemnie prostopadłych osi . Czyli mają 6 stopni swobody ( 3 translacje , 2 rotacyjne i 1 oscylacyjny ) . A zatem dla gazów dwuatomowych przy założeniu . że cząstki nie wykonują oscylacji : = 7/5 = 1,4

Założenie powyższe jest uzasadnione , ponieważ w temperaturach pokojowych ruchy oscylacyjne dla większości lekkich cząstek dwuatomowych są całkowicie "zamrożone" . Uruchomienie oscylacji w wyższych temperaturach powoduje obniżenie wartości , natomiast zamrożenie ruchów rotacyjnych cząstki występującej w niższych temperaturach prowadzi do wzrostu wartości

Ponieważ powietrze z większości składa się z tlenu i azotu można przyjąć że wartość dla powietrza wynosi 1,4 . Natomiast dla powietrza wyznaczone doświadczalnie wynosi : 1,1704440,0084.

W rzeczywistości otrzymana doświadczalnie wartość jest różna od przewidywań teoretycznych . Wynika to z wielu uproszczeń występujących w tej klasycznej teorii kinetyczno - molekularnej. Jak wiadomo teoria ta nie uwzględnia rotacyjnych stopni swobody atomów w cząsteczce . Nie uwzględnia także elektronowych i jądrowych stopni swobody w atomie . Wpływ może mieć także fakt, że powietrze oprócz azotu i tlenu składa się dodatkowo z 1% innych gazów .

p

V

V

V

T

p

---