POJĘCIE GAZU DOSKONAŁEGO
W fizyce bardzo często mamy do czynienia z modelami - idealizacjami pewnych zjawisk. Dzięki nim możemy chociaż w przybliżeniu opisywać pewne procesy, które zachodzą w rzeczywistości. W tym rozdziale będziemy częto posługiwać się modelem gazu doskonałego:
Gaz doskonały - definicja
Jedynym rodzajem oddziaływań cząsteczek w gazie doskonałym są zderzenia sprężyste pomiędzy cząsteczkami oraz ze ściankami naczynia.
Objętość cząsteczek gazu doskonałego jest zaniedbywalnie mała w porównaniu z objętością naczynia.
Gazy rzeczywiste zachowują się jak gaz doskonały tylko w odpowiednich warunkach: w wysokiej temperaturze (energia kinetyczna cząsteczek jest na tyle duża, że można zaniedbać energię oddziaływań elektromagnetycznych) i niskim ciśnieniu (gaz jest rozrzedzony, a dzięki temu rozmiary cząsteczek są małe w porównaniu do odległości między nimi).
Model ten ma zastosowanie do wszystkich gazów rzeczywistych, ale istnieją granice jego zastosowania, z którymi wiąże się kolejne pojęcie:
Temperatura zera bezwzględnego - definicja
Jest to najniższa temperatura, do której możemy się zbliżać, ale jej osiągnięcie jest niemożliwe (ciśnienie i objętość musiałyby być równe zeru). W temperaturze tej zanika całkowicie ruch cząsteczek. Temperatura ta jest równa -273,15 oC lub 0 K (kelwinów).
Skala Kelvina nazywana jest również bezwzględną skalą temperatur. Jednostkowy przyrost temperatury w obydwu skalach jest taki sam:
Δt = 1oC = 1K
T = t(oC) + 273,15
T - temp. w kelwinach
RÓWNANIE STANU GAZU DOSKONAŁEGO - RÓWNANIE CLAPEYRONA
Równanie Clapeyrona pokazuje zależność pomiędzy trzema jego właściwościami, które pozwalaja opisać go oraz wpływają na jego zachowanie: ciśnieniem, temperaturą i objętością.
Z teorii kinetyczno-molekularnej wiemy, że:
p = (2N)/(3V) .Eśr
W fizyce jest wiele różnorakich stałych, niektóre z nich nie mają nawet nazwy. Podczas wyprowadzania równania Clapeyrona pojawi się ich kilka. Jedną z nich jest stała oznaczana symbolem C. Wyraża ona stosunek energii średniej cząsteczek gazu do jego temperatury:
C=Eśr / T
Zatem:
p = (2N)/(3V) .Eśr i Eśr = T . C =>p = (2NTC)/(3V)
Wprowadzamy kolejną stałą - k - zwaną stałą Boltzmana:
k = 2/3 . C
I po podstawieniu otrzymujemy:
p = (kNT) / V
Po obustronnym pomnożeniu przez V i podzieleniu przez T otrzymujemy:
(pV)/T = kN
Widać już, że iloraz iloczyny ciśnienia i objętości przez temperaturę (pV)/T jest zawsze stały, ponieważ k jest stałą, a i N=const (liczba cząsteczek nie ulega zmianie).
Rozpatrzmy teraz 1 mol gazu (mol to nie taki denerwujący owad, ale jednostka liczności materii, to powinno być na chemii :) Dla 1 mola gazu N = NA (NA - stałą Avogadro) - w jednym molu substancji jest zawsze tyle samo cząsteczek - 6,022 . 1023 - i to jest właśnie NA. Zatem można zapisać:
(pV)/T = kNA
Pojawia się już ostatnia stała w tym wyprowadzeniu, ale stała bardzo ważna - R - stała gazowa (R = 8,31 J / (mol . K)) :
R = kNA
Zatem po podstawieniu:
(pV)/T = R
Dla n moli gazu:
(pV)/T = nR
Po przekształceniu otrzymujemy równanie Clapeyrona:
pV = nRT
n = m/M jak wiadomo z chemii :) gdzie m to masa substacji, a M to masa molowe tej substancji. Zatem można zapisać jeszcze jedną postać tego równania:
PRZEMIANY GAZOWE
Dla wszystkich przemian prawdziwa jest zależność:
(p1V1)/T1 = (p1V2)/T2
czyli, innymi słowy stosunek iloczyny ciśnienia i objętości do temperatury gazu jest zawsze taki sam.
Przemiana izotermiczna jest nazywana również prawem Boyle'a - Mariotte'a. Jak sama nazwa wskazuje, w przemianie tej temperatura nie ulega zmianie:
T = const
w związku z tym również:
pV = const
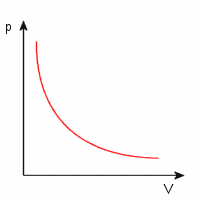
Wykres ten przedstawia zależność ciśnienia od objętośći dla gazu w przemianie izotermicznej. Krzywa ta nazywa się izotermą.
Przemiana izohoryczna stałej masy gazu charakteryzuje się niezmiennością objętości. Przyrost ciśnienia jest wprost proporcjonalny do przyrostu temperatury.
V = const
p / T = const
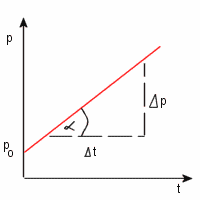
Równanie tej prostej, zwanej również izochorą można zapisać :
p = (Δp / Δt) . t + p0
Na poniższych rysunkach przedstawione są przemiany izobaryczne wody i pary wodnej w układzie h-s (entalpia właściwa - entropia właściwa) i T-s (temperatura - entropia właściwa) na tle linii nasycenia i stałego stopnia suchości pary.
Przemiana izobaryczna zachodzi, gdy ciśnienie stałej masy gazu nie ulega zmianie. Przyrots objętości jest wprost proporcjonalny do przyrostu temperatury.
p = const
V / T = const
Równaniej tej prostej zwanej izobarą można zapisać:
V = (ΔV / Δt) . t + V0
Wyszukiwarka
Podobne podstrony:
promieniowanie rentgnenowskie, Akademia Morska Szczecin, SEMESTR II, Fizyka, sciaga fiza
efekt comptona2, Akademia Morska Szczecin, SEMESTR II, Fizyka, sciaga fiza
Pole elektryczne, Akademia Morska Szczecin, SEMESTR II, Fizyka, sciaga fiza
Mechanizmy opornosci elektrycznej, Akademia Morska Szczecin, SEMESTR II, Fizyka, sciaga fiza
model atomu wedlug Bohra2, Akademia Morska Szczecin, SEMESTR II, Fizyka, sciaga fiza
model osnowy przedodnictwa2, Akademia Morska Szczecin, SEMESTR II, Fizyka, sciaga fiza
Czdosw1, Akademia Morska Szczecin, SEMESTR II, Fizyka, FIZYKA- SPRAWOZDANIA
Pomiar siły elektromotorycznej ogniwa, Akademia Morska Szczecin, SEMESTR II, Fizyka, I semestr
Wyznaczanie temperatury Curie ferrytu [wnioski], Akademia Morska Szczecin, SEMESTR II, Fizyka, I sem
Fizyka-6, Akademia Morska Szczecin, SEMESTR II, Fizyka, FIZYKA- SPRAWOZDANIA
CZ DO WIADCZALN1, Akademia Morska Szczecin, SEMESTR II, Fizyka, FIZYKA- SPRAWOZDANIA
Pomiar rezystancji metodą mostkową, Akademia Morska Szczecin, SEMESTR II, Fizyka, I semestr
w 02 Badanie rezonansu w o, Akademia Morska Szczecin, SEMESTR II, Fizyka, FIZYKA- SPRAWOZDANIA
w 06 promieniowanie - abso, Akademia Morska Szczecin, SEMESTR II, Fizyka, FIZYKA- SPRAWOZDANIA
Cz do wiadczalna, Akademia Morska Szczecin, SEMESTR II, Fizyka, FIZYKA- SPRAWOZDANIA
Wyznaczanie temperatury Curie ferrytu, Akademia Morska Szczecin, SEMESTR II, Fizyka, I semestr
DROGA I PRĘDKOŚĆ STATKU, Akademia Morska Szczecin, SEMESTR II, NAWIGACJA, wykłady II sem
POLE MAGNETYCZNE STATKU, Akademia Morska Szczecin, SEMESTR II, NAWIGACJA, wykłady II sem
Droga transportowa sciaga1, Akademia Morska Szczecin, SEMESTR II
więcej podobnych podstron