ĆWICZENIE

Z

MECHANIKI PŁYNÓW

„KORYTA I PRZELEWY”

ZADANIE 1.

Zaprojektować przekrój koryta otwartego, jeżeli:

Q = 12,7

h = 1,50

I = 0,92 ‰ = 0,00092

n = 0,022

nachylenie skarp 1:m = 1:3

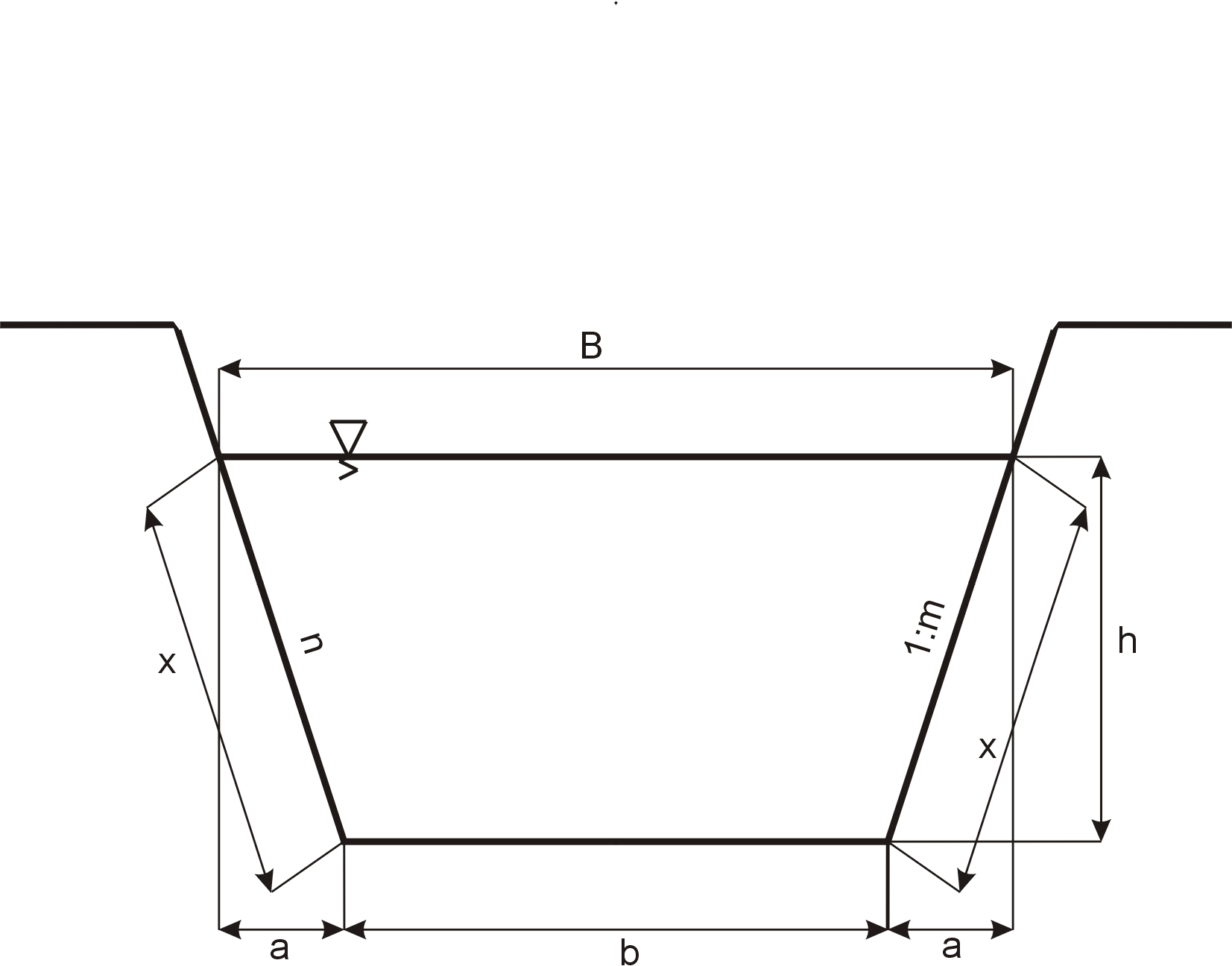
Sporządzić krzywą konsumcyjną.

1. Zakładam, że projektowane koryto jest symetryczne i pryzmatyczne.

2. Obliczam pole powierzchni przekroju przepływowego
   :

a = mh

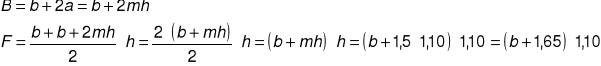
Rozwiązaniem tego równania jest zależność b od Q.

3. Obliczam obwód zwilżony
   :

Rozwiązaniem tego równania jest zależność b od Q.

4. Obliczam promień hydrauliczny
   :

5. Obliczam przepływ
   :

wzór:

6. Przygotowanie wykresu:

Zakładam, że b = …

b	F	U	Rh	Q
0,00	6,75	9,48	0,71	7,42
1,00	8,25	10,48	0,79	9,70
2,00	9,75	11,48	0,85	12,06
3,00	11,25	12,48	0,90	14,47
4,00	12,75	13,48	0,95	16,94
2,10	9,90	11,58	0,85	12,30
2,20	10,05	11,68	0,86	12,54
2,30	10,20	11,78	0,87	12,78
2,21	10,07	11,69	0,86	12,56
2,22	10,08	11,70	0,86	12,58
2,23	10,10	11,71	0,86	12,61
2,24	10,11	11,72	0,86	12,63
2,25	10,13	11,73	0,86	12,66
2,26	10,14	11,74	0,86	12,68
2,27	10,16	11,75	0,86	12,70
2,28	10,17	11,76	0,86	12,73

7. Sporządzam wykres
   wg danych z tabeli:

8. Odczytuję szerokość dna koryta
   z wykresu:

9. Wykonuję obliczenia sprawdzające:

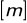
10. Na podstawie otrzymanych wyników obliczam szerokość koryta na poziomie zwierciadła wody
    :

11. Wymiary przekroju koryta otwartego:

• Szerokość dna koryta -
  
  

• Szerokość koryta na poziomie zwierciadła wody -
  
  

• Wysokość od zwierciadła wody do dna -
  
  

• Długość skarpy z jednej i drugiej strony -
  
  

12. Krzywa konsumcyjna
    - przygotowanie:

h	Q		a	B	F	x	U	Rh
0	0,000		0	2,27	0	0,000	2,270	0,000
0,1	0,071		0,3	2,87	0,257	0,316	2,902	0,089
0,2	0,236		0,6	3,47	0,574	0,632	3,535	0,162
0,3	0,490		0,9	4,07	0,951	0,949	4,167	0,228
0,4	0,838		1,2	4,67	1,388	1,265	4,800	0,289
0,5	1,284		1,5	5,27	1,885	1,581	5,432	0,347
0,6	1,837		1,8	5,87	2,442	1,897	6,065	0,403
0,7	2,503		2,1	6,47	3,059	2,214	6,697	0,457
0,8	3,288		2,4	7,07	3,736	2,530	7,330	0,510
0,9	4,200		2,7	7,67	4,473	2,846	7,962	0,562
1	5,246		3	8,27	5,27	3,162	8,595	0,613
1,1	6,431		3,3	8,87	6,127	3,479	9,227	0,664
1,2	7,763		3,6	9,47	7,044	3,795	9,859	0,714
1,3	9,248		3,9	10,07	8,021	4,111	10,492	0,764
1,4	10,891		4,2	10,67	9,058	4,427	11,124	0,814
1,5	12,699		4,5	11,27	10,155	4,743	11,757	0,864
1,6	14,679		4,8	11,87	11,312	5,060	12,389	0,913
1,62	15,096		4,86	11,99	11,5506	5,123	12,516	0,923
1,7	16,836		5,1	12,47	12,529	5,376	13,022	0,962
1,8	19,175		5,4	13,07	13,806	5,692	13,654	1,011
1,9	21,703		5,7	13,67	15,143	6,008	14,287	1,060
2	24,425		6	14,27	16,54	6,325	14,919	1,109
2,1	27,347		6,3	14,87	17,997	6,641	15,552	1,157
2,2	30,475		6,6	15,47	19,514	6,957	16,184	1,206
2,3	33,813		6,9	16,07	21,091	7,273	16,816	1,254

13. Krzywa konsumcyjna
    :




ZADANIE 2.

Obliczyć szerokość przelewu „
” usytuowanego w zaprojektowanym korycie w przypadku, gdy jest to przelew o szerokiej koronie.

DANE:

- wysokość piętrzenia p = 0,35


- dopuszczalne spiętrzenie na przelewie Δh = 0,30


- przepływ Q = 12,7


- charakterystyka kształtu przelewu φ: φ = 0,88 [wartość współczynnika odczytana z tabeli do obliczeń przelewów o szerokiej koronie - przy ściętej krawędzi wlotowej]

h_d=1,5 [m]

h_g=1,8 [m]

h_kr=0,945 [m]

h_d>h_kr

1,5>0,945 => ruch spokojny

h_g>h_kr

1,8>0,945 => ruch spokojny

- współczynnik prędkości α α = 1,05

- szerokość dna koryta b = 2,6








1. Wyznaczam głębokość wody dolnej
   dla przepływu
   z krzywej konsumcyjnej:





2. Obliczam głębokość wody górnej
   przez dodanie dopuszczalnego spiętrzenia
   do głębokości dolnej wody
   :





3. Obliczam grubości warstwy wody
   przelewającej się przez przelew jako różnicy między głębokością górnej wody
   a wysokością piętrzenia
   :





4. Obliczam pole powierzchni przekroju poprzecznego koryta na górnym stanowisku:













5. Obliczam pole powierzchni przekroju poprzecznego koryta na dolnym stanowisku:













6. Obliczam prędkości przepływu
   i
   :









7. Obliczam wysokość prędkości
   na górnym stanowisku:





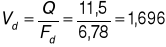
8. Obliczam wysokość
   :





9. Obliczam wysokość wody dolnej
   nad przelewem:





10. Zakładam, że przelew jest ZATOPIONY:







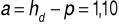
11. Sprawdzamy warunki zatopienia:

• Obliczam przepływ jednostkowy:

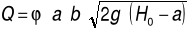
• Obliczam parametry ruchu krytycznego:

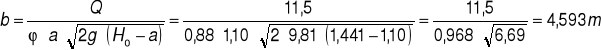
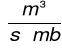
• Obliczam przewyższenie
  :

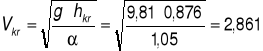
• Warunki zatopienia:

Wniosek:

Przelew jest NIEZATOPIONY.

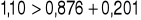
[m]

Odpowiedź:

Szerokość przelewu

.

ZADANIE 3.

Dla zaprojektowanego przelewu obliczyć głębokość i długość niecki wypadowej.

DANE:

b_j = 0,499

F_g = 13,81

H_p = h_g = 1,80

Q = 12,7

współczynnik prędkości φ = 0,95 [dla wypływu spod zasuwy na płycie równo z dnem]

współczynnik prędkości φ_s = 0,85 [dla wyjścia z niecki zakończonej pionową ścianką]

współczynnik St. Venanta α = 1,05

Obliczenia rozpoczynam od przepływu

.

1. Obliczam prędkość dopływową
   :

2. Obliczam wysokość prędkości
   przed zasuwą:

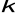
3. Obliczam wysokość energii
   przed zasuwą:

4. Obliczam przepływ jednostkowy
   w przekroju zasuwy:

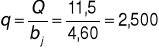
5. Obliczam pierwszą głębokość sprzężoną
   (metoda wzorów przybliżonych):

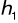
6. Obliczam drugą głębokość sprzężoną
   :

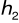
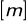
7. Obliczam przewyższenie linii energii
   na wyjściu z niecki ponad poziom dolnej wody:

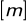
- odczytujemy z krzywej konsumcyjnej dla danego Q;

tutaj: dla



.

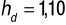
8. Obliczam wysokość prędkości
   w przekroju drugiej głębokości sprzężonej
   :

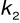
9. Obliczam przewyższenie poziomu wody
   na wyjściu z niecki ponad poziom dolnej wody:

10. Obliczam głębokość niecki
    :

- odczytujemy z krzywej konsumcyjnej dla danego Q;

tutaj: dla



.

Stosując algorytm [zrobiony w arkuszu kalkulacyjnym] od punktu 1 - 10 wypełniam tabelę.

Q	Fg	vg	k	E	q	h1	h2	hd	delta zo	k2	delta z	do		do
0,10	13,810	0,007	0,000003	1,800	0,200	0,035	0,475	0,100	0,297	0,010	0,288	0,087		0,09
0,20	13,810	0,014	0,000011	1,800	0,401	0,071	0,661	0,200	0,297	0,020	0,278	0,184		0,18
0,50	13,810	0,036	0,000070	1,800	1,002	0,177	1,015	0,300	0,826	0,052	0,774	-0,059		-0,06
0,80	13,810	0,058	0,000180	1,800	1,603	0,284	1,257	0,400	1,190	0,087	1,103	-0,246		-0,25
1,30	13,810	0,094	0,000474	1,800	2,605	0,461	1,559	0,500	2,011	0,149	1,861	-0,803		-0,80
1,80	13,810	0,130	0,000909	1,801	3,607	0,639	1,793	0,600	2,677	0,217	2,461	-1,268		-1,27
3,30	13,810	0,239	0,003056	1,803	6,613	1,170	2,303	0,800	5,062	0,441	4,620	-3,117		-3,12

Maksymalna głębokość
jest dla przepływu

.

W całym zakresie zmienności Q głębokość sprzężona h₂ jest większa od głębokości dolnej wody h_d. Niecka potrzebna w całym zakresie Q.

11. Obliczam głębokość niecki dla współczynnika zatopienia
    , np.
    dla przepływu
    
    .

12. Dla obliczonej głębokości niecki wykonuję obliczenia sprawdzające zatopienie odskoku:

• Wysokość energii przed zasuwą względem dna niecki dla przepływu
  
  :

• Pierwsza głębokość sprzężona:

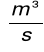
• Druga głębokość sprzężona:

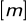
• Przewyższenie linii energii na wyjściu z niecki ponad poziom dolnej wody:

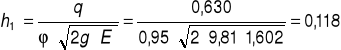
• Wysokość prędkości w przekroju drugiej głębokości sprzężonej:

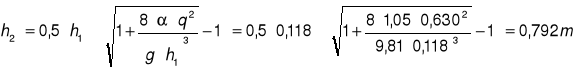
• Przewyższenie poziomu wody na wyjściu z niecki ponad poziom dolnej wody:

13. Obliczam współczynnik zatopienia odskoku:

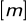
14. Obliczam wysokość podniesienia zasuwy przy przepływie
    
    :

Z tabeli odczytano
, stąd

, czyli zasuwa przy przepływie

powinna być podniesiona na wysokość

ponad poziom progu.

15. Obliczam długość niecki wypadowej:

Przyjmuję, że długość niecki jest równa długości odskoku.

• wg Smetany:

• wg Safraneza:

Przyjmuję większą wartość: L=3,546

2

---